Cours 8 Analyse syntaxique descendante ascendante par programmation

Cours 8 Analyse syntaxique - descendante - ascendante - par programmation dynamique

Analyse syntaxique Parsing Entrées : une phrase étiquetée et une grammaire algébrique Sorties : le ou les arbres de dérivation de la phrase Algorithmes Descendants Ascendants Programmation dynamique Cascade de transducteurs

Exemple de grammaire algébrique P --> GN <disparaître> P --> GN <empirer> P --> GN <orchestrer> GN P --> GN <aimer> GN GN --> Det N GN --> Npr Det --> <le> Det --> <ce> Det --> <un> Det --> tous les Det --> toutes les N --> <mélodie> N --> <corruption> N --> <orchestre> N --> <empire> Npr --> Luc Npr --> Anne

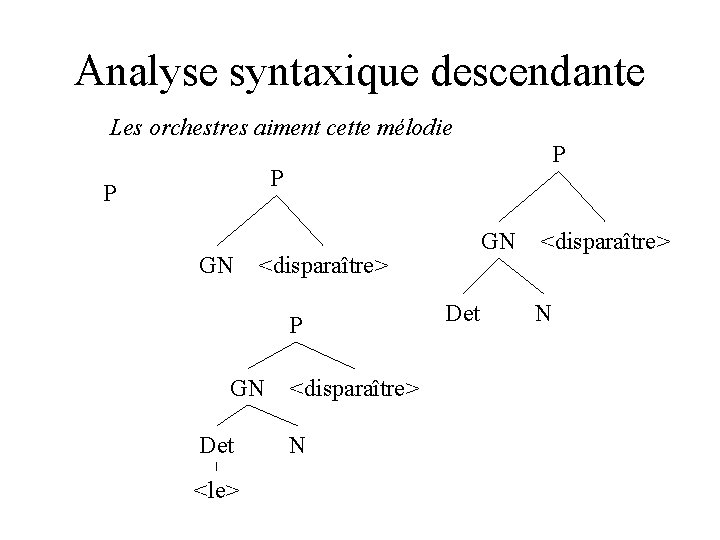
Analyse syntaxique descendante Les orchestres aiment cette mélodie P P P GN <disparaître> P GN Det <le> GN <disparaître> N Det <disparaître> N

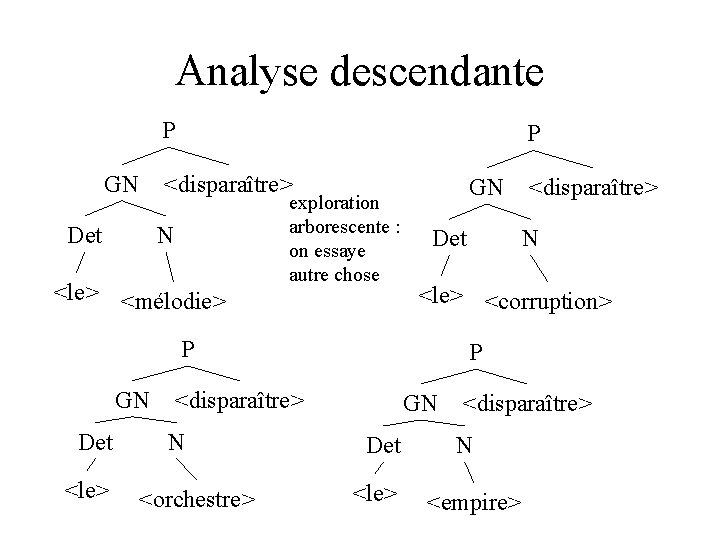
Analyse descendante P GN P <disparaître> Det N <le> <mélodie> exploration arborescente : on essaye autre chose GN Det <le> P <disparaître> N <orchestre> N <le> <corruption> P GN <disparaître> GN Det <le> <disparaître> N <empire>

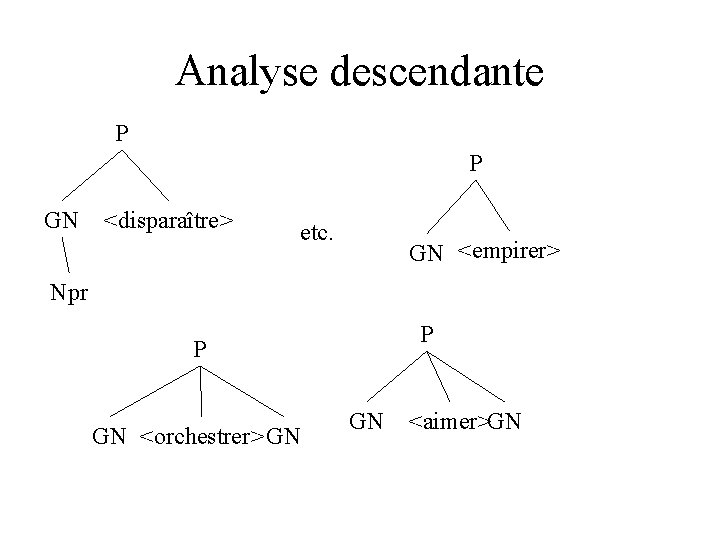
Analyse descendante P P GN <disparaître> etc. GN <empirer> Npr P P GN <orchestrer> GN GN <aimer>GN

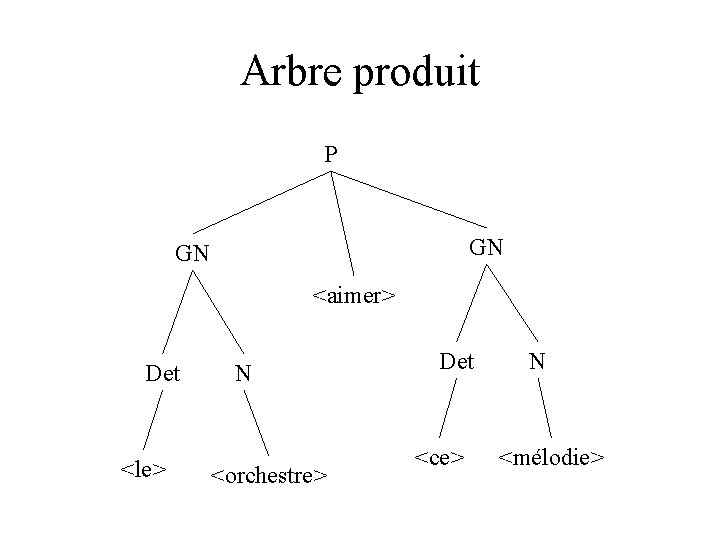
Arbre produit P GN GN <aimer> Det <le> N <orchestre> Det <ce> N <mélodie>

Analyse descendante phrase. desc(arbre, feuille. Courante, token. Courant) : pour chaque feuille 1 à partir de feuille. Courante symbole = feuille 1. étiquette si symbole est terminal si symbole est compatible avec token = phrase. suivant(token) sinon détruire arbre ; sortir de la fonction sinon si symbole est une variable pour chaque règle dont le membre gauche est symbole copie. Arbre = arbre. copier() feuille 2 = équivalent de feuille 1 dans copie. Arbre. ajouter(règle, feuille 2) feuille 3 = copie. Arbre. premier. Fils(feuille 2) phrase. desc(copie. Arbre, feuille 3, token) sortir de la fonction arbre. écrire()

Exemple (1/8) L'orchestre aime cette mélodie desc(P, P, L') desc(P(GN disparaître), GN, L') desc(P(GN(Det N) disparaître), Det, L') desc(P(GN(Det(le) N) disparaître), le, L') desc(P(GN(Det(le) N(mélodie)) disparaître), mélodie, orchestre) desc(P(GN(Det(le) N(corruption)) disparaître), corruption, orchestre) desc(P(GN(Det(le) N(orchestre)) disparaître), disparaître, aime) desc(P(GN(Det(le) N(empire)) disparaître), empire, orchestre)

Exemple (2/8) desc(P(GN(Det(ce) N) disparaître), ce, L') desc(P(GN(Det(un) N) disparaître), un, L'). . . desc(P(GN(Npr) disparaître), Npr, L')

Exemple (3/8) desc(P(GN empirer), GN, L') desc(P(GN(Det N) empirer), Det, L') desc(P(GN(Det(le) N) empirer), le, L') desc(P(GN(Det(le) N(mélodie)) empirer), mélodie, orchestre) desc(P(GN(Det(le) N(corruption)) empirer), corruption, orchestre) desc(P(GN(Det(le) N(orchestre)) empirer), empirer, aime) desc(P(GN(Det(le) N(empire)) empirer), empire, orchestre)

Exemple (4/8) desc(P(GN(Det(ce) N) empirer), ce, L') desc(P(GN(Det(un) N) empirer), un, L'). . . desc(P(GN(Npr) empirer), Npr, L')

Exemple (5/8) desc(P(GN ochestrer GN), GN, L') desc(P(GN(Det N) orchestrer GN), Det, L') desc(P(GN(Det(le) N) orchestrer GN), le, L') desc(P(GN(Det(le) N(mélodie)) orchestrer GN), mélodie, orchestre). . . desc(P(GN(Det(ce) N) orchestrer GN), ce, L') desc(P(GN(Det(un) N) orchestrer GN), un, L'). . . desc(P(GN(Npr) orchestrer GN), Npr, L')

Exemple (6/8) desc(P(GN aimer GN), GN, L') desc(P(GN(Det N) aimer GN), Det, L') desc(P(GN(Det(le) N) aimer GN), le, L') desc(P(GN(Det(le) N(mélodie)) aimer GN), mélodie, orchestre) desc(P(GN(Det(le) N(corruption)) aimer GN), corruption, orchestre) desc(P(GN(Det(le) N(orchestre)) aimer GN), aimer, aime) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det N)), Det, cette)

Exemple (7/8) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det N)), Det, cette) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det(le) N)), le, cette) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det(ce) N)), cette) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det(ce) N(mélodie))), mélodie) desc(P(GN(Det(le) N(orchestre)) aimer GN(Det(ce) N(corruption))), corruption, mélodie). . .

Exemple (8/8) desc(P(GN(Det(un) N(orchestre)) aimer GN(Det(un) N)), un, cette). . . desc(P(GN(Det(le) N(orchestre)) aimer GN(Npr)), Det, cette) desc(P(GN(Det(le) N(empire)) aimer GN), empire, orchestre) desc(P(GN(Det(ce) N) aimer GN), ce, L') desc(P(GN(Det(un) N) aimer GN), un, L'). . . desc(P(GN(Npr) aimer GN), Npr, L')

Inconvénients On utilise peu le texte Avec Les orchestres aiment cette mélodie, les 10 premiers arbres contiennent disparaître, qui ne figure pas dans la phrase On construit plusieurs fois les mêmes sous-arbres Le sous-arbre pour Les orchestres est construit 4 fois et détruit 3 fois Boucle en cas de récursivité gauche Une règle comme GN --> GN Adj met l'algorithme dans une boucle infinie

Analyse syntaxique ascendante Les orchestres aiment cette mélodie <le> <orchestre> <aimer> <ce> <mélodie> <le> <orchestrer> <aimer> <ce> <mélodie> Det <le> <orchestre> <aimer> <ce> <mélodie> N <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 1) Det <le> <orchestre> <aimer> <ce> <mélodie> N <le> <orchestre> <aimer> <ce> <mélodie> Det <le> <orchestrer> <aimer> <ce> <mélodie> N <le> <orchestrer> <aimer> <ce> <mélodie>

Analyse ascendante (itération 2) Det N <le> <orchestre> <aimer> <ce> <mélodie> Det N <le> <orchestre> <aimer> <ce> <mélodie> N Det <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 2) N N <le> <orchestre> <aimer> <ce> <mélodie> Det Det <le> <orchestrer> <aimer> <ce> <mélodie> Det N <le> <orchestrer> <aimer> <ce> <mélodie>

Analyse ascendante (itération 2) Det N <le> <orchestrer> <aimer> <ce> <mélodie>

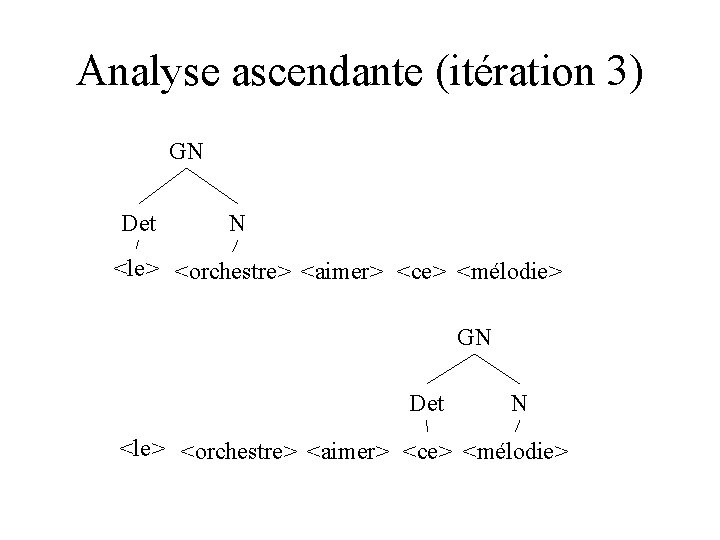
Analyse ascendante (itération 3) GN Det N <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 3) Det N Det <le> <orchestre> <aimer> <ce> <mélodie> Det N N <le> <orchestre> <aimer> <ce> <mélodie> N Det N <le> <orchestre> <aimer> <ce> <mélodie>

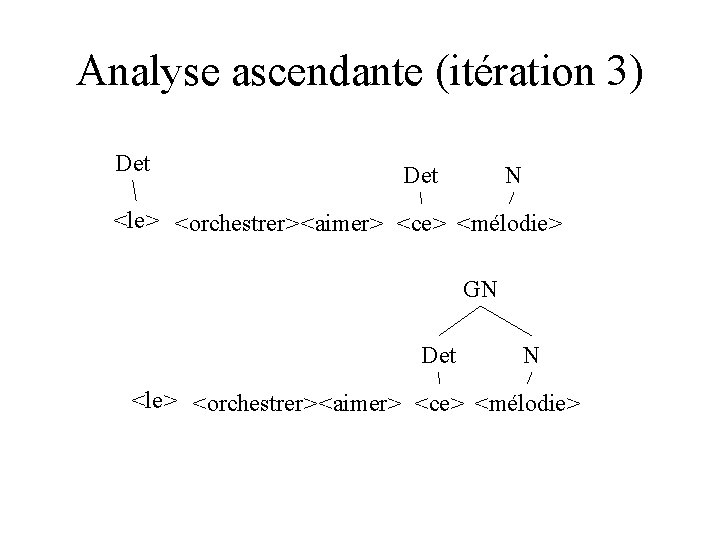
Analyse ascendante (itération 3) Det N <le> <orchestrer> <aimer> <ce> <mélodie> GN Det N <le> <orchestrer> <aimer> <ce> <mélodie>

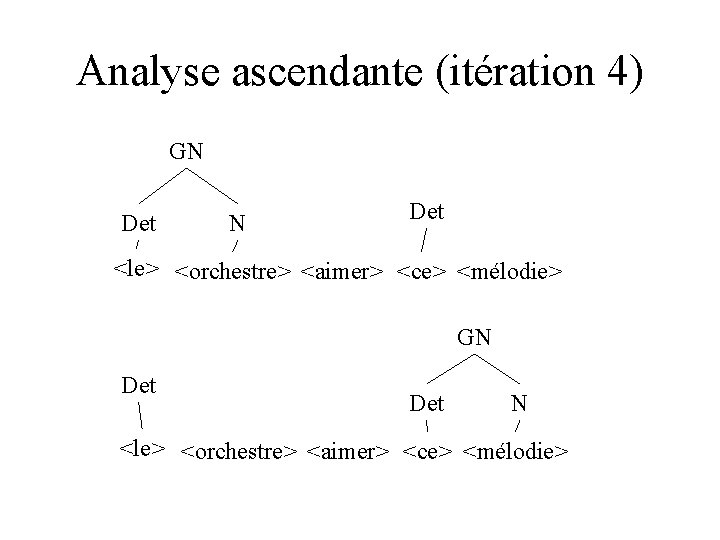
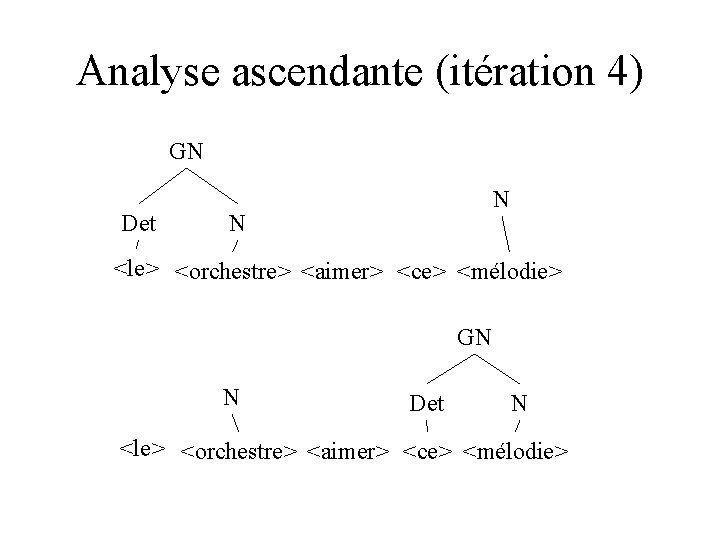
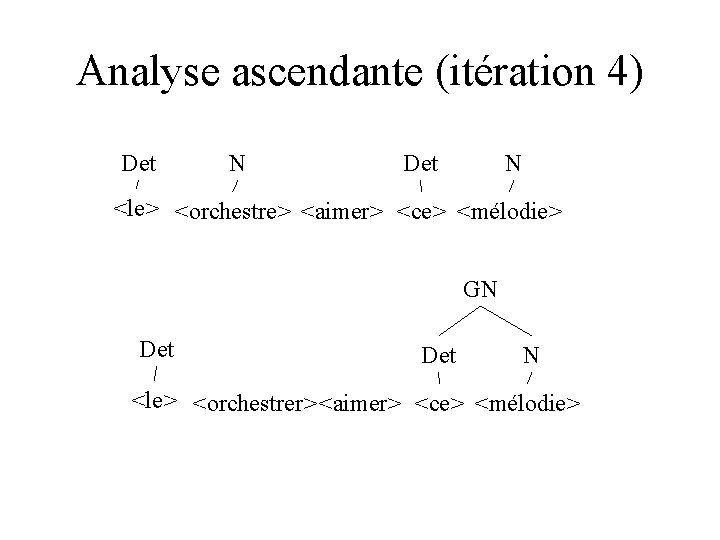
Analyse ascendante (itération 4) GN Det <le> <orchestre> <aimer> <ce> <mélodie> GN Det N <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 4) GN Det N N <le> <orchestre> <aimer> <ce> <mélodie> GN N Det N <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 4) Det N <le> <orchestre> <aimer> <ce> <mélodie> GN Det N <le> <orchestrer> <aimer> <ce> <mélodie>

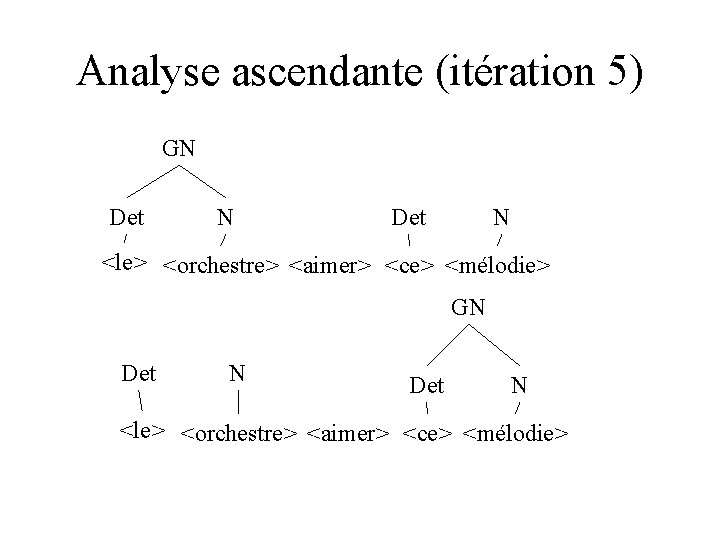
Analyse ascendante (itération 5) GN Det N <le> <orchestre> <aimer> <ce> <mélodie>

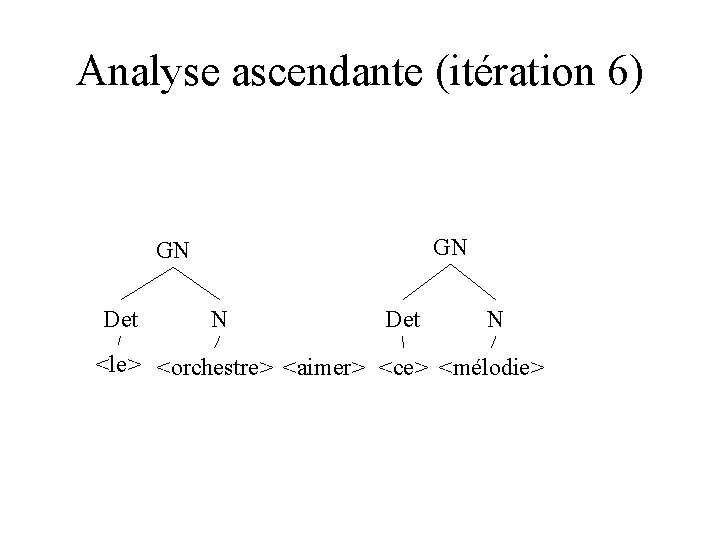
Analyse ascendante (itération 6) GN GN Det N <le> <orchestre> <aimer> <ce> <mélodie>

Analyse ascendante (itération 7) P GN GN Det N <le> <orchestre> <aimer> <ce> <mélodie>

Algorithme (1/2) ens. Seq. Arbres = un ensemble de séquences d'arbres vide pour chaque combinaison de terminaux compatible avec phrase ens. Seq. Arbres. ajouter. Seq. Arbres(combinaison) tant que ens. Seq. Arbres n'est pas vide nouv. Ens. Seq. Arbres = un ensemble de séquences d'arbres vide pour chaque seq. Arbres dans ens. Seq. Arbres seq. Racines = seq. Arbres. seq. Racines() pour chaque facteur de seq. Racines pour chaque règle dont le membre droit corresp. à facteur copie. Seq. Arbres = seq. Arbres. copier() copie. Seq. Arbres. ajouter(facteur, règle) nouv. Ens. Seq. Arbres. ajouter(copie. Seq. Arbres)

Algorithme (2/2) pour chaque seq. Arbres dans nouv. Ens. Seq. Arbres si seq. Arbres est un arbre et si sa racine est l'axiome seq. Arbres. écrire() nouv. Ens. Seq. Arbres. supprimer(seq. Arbres) ens. Seq. Arbres = nouv. Ens. Seq. Arbres

Inconvénients On utilise peu la grammaire Avec Les orchestres aiment cette mélodie, toutes les séquences qui contiennent <orchestrer> suivi de <aimer> sont incompatibles avec la grammaire

L'algorithme d'Earley (1970) Analyse descendante Sauvegarde dans un tableau tous les résultats intermédiaires réutilisables (programmation dynamique) Tableau indicé par les tokens de la phrase Phrase : Les orchestres aiment cette mélodie Indices : 0 1 2 3 4 Pour chaque indice, le tableau contient un ensemble de sous-arbres correspondant à des analyses partielles On remplit le tableau de gauche à droite, sans retours en arrière On ne détruit jamais des sous-arbres déjà créés Pour construire les arbres de dérivation, on combine les sous-arbres du tableau 5

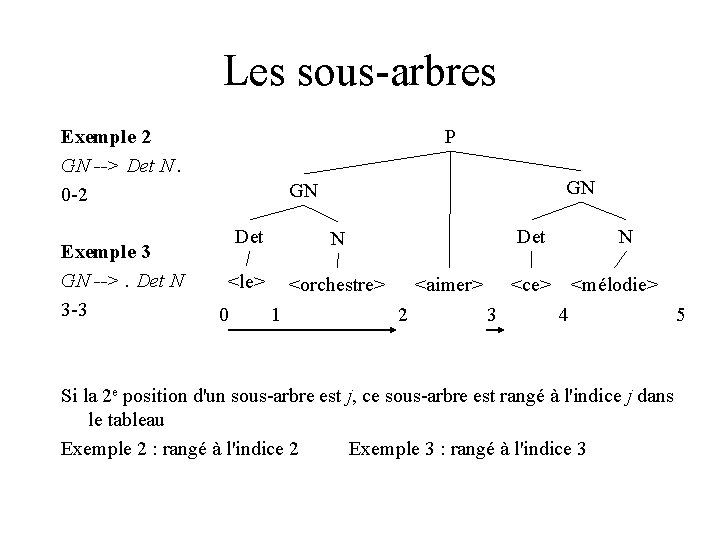
Les sous-arbres Un sous-arbre est représenté par - une règle pointée (le point indique jusqu'où on a analysé) - deux positions dans la phrase, correspondant : - au début de la règle - et au point jusqu'où on a analysé Exemple 1 P --> GN <aimer>. GN 0 -3 0 P GN GN Det N <le> <orchestre> 1 Det <aimer> 2 N <ce> <mélodie> 3 4 5

Les sous-arbres P Exemple 2 GN --> Det N. 0 -2 Exemple 3 GN -->. Det N 3 -3 GN GN Det N <le> <orchestre> 0 1 Det <aimer> 2 N <ce> <mélodie> 3 4 5 Si la 2 e position d'un sous-arbre est j, ce sous-arbre est rangé à l'indice j dans le tableau Exemple 2 : rangé à l'indice 2 Exemple 3 : rangé à l'indice 3

L'algorithme On parcourt le tableau de gauche à droite Quand on est à l'indice i, on parcourt les sous-arbres et on crée de nouveaux sous-arbres à l'indice i (queue FIFO) et à l'indice i + 1 On suppose que l'axiome de la grammaire apparaît une seule fois, dans une règle P 0 --> P Début P 0 -->. P 0 -0 Fin P 0 --> P. 0 -n (n = nombre de tokens dans la phrase) Règle pointée complétée : règle dont le point est à la fin

L'algorithme analyseur. table[0]. enfiler(P 0 -->. P, 0, 0) pour i de 0 à n pour chaque sous. Arbre dans table[i] si sous. Arbre. complétée() analyseur. compléter(sous. Arbre) sinon si sous. Arbre. prochain. Symbole() est terminal analyseur. vérifier(sous. Arbre) sinon analyseur. prédire(sous. Arbre) si analyseur. table[n]. contient(P 0 --> P. , 0, n) analyseur. construire. Arbres(n)

L'algorithme compléter(B --> w. , j, k) : pour chaque (A --> u. B v, i, j) dans table[j] table[k]. enfiler(A --> u B. v, i, k) vérifier(A --> u. t v, i, j) : si t correspond à token[j] table[j + 1]. enfiler(A --> u t. v, i, j + 1) prédire(A --> u. B v, i, j) : pour chaque (B --> w) dans règles(B) table[j]. enfiler(B -->. w, j, j)