COURS 03 Chapitre 3 Bobines noyau de fer

COURS 03 Chapitre - 3 Bobines à noyau de fer 1 - Analogies électrique/magnétique 2 - Bobines monophasées 2. 1 - Circuits magnétiques 2. 2 - Allure du courant absorbé 2. 3 - Schéma équivalent 3 - Bobines triphasées 1

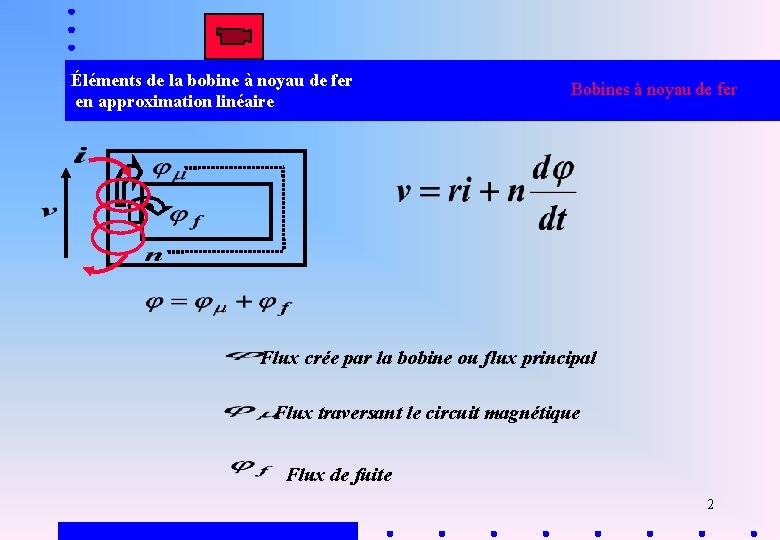
Éléments de la bobine à noyau de fer en approximation linéaire Bobines à noyau de fer Flux crée par la bobine ou flux principal Flux traversant le circuit magnétique Flux de fuite 2

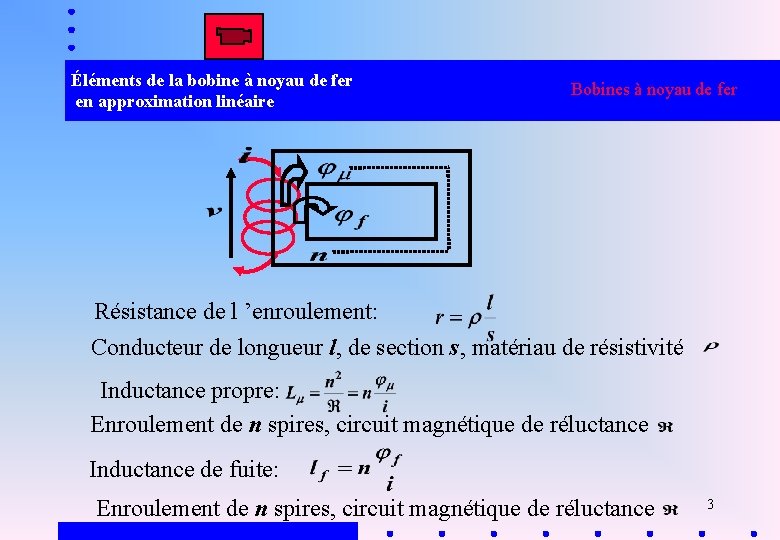
Éléments de la bobine à noyau de fer en approximation linéaire Bobines à noyau de fer Résistance de l ’enroulement: Conducteur de longueur l, de section s, matériau de résistivité Inductance propre: Enroulement de n spires, circuit magnétique de réluctance Inductance de fuite: Enroulement de n spires, circuit magnétique de réluctance 3

Page 9 1 -Relation entre les grandeurs magnétiques et électriques Bobines à noyau de fer Relations entre le flux (ou induction) et la tension et Expression de Bmax D ’où Relations entre le flux et le courant 4

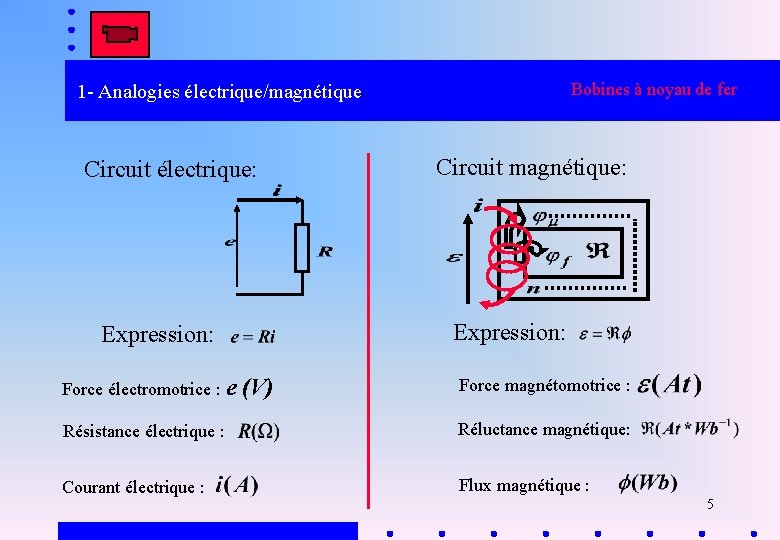
Bobines à noyau de fer 1 - Analogies électrique/magnétique Circuit électrique: Expression: Circuit magnétique: Expression: Force électromotrice : e (V) Force magnétomotrice : Résistance électrique : Réluctance magnétique: Courant électrique : Flux magnétique : 5

Page 8 Bobines à noyau de fer 1 - Analogies électrique/magnétique circuit électrique D d p ou tension (V) e i R= 1 l s. S courant (A) résistance (W) conductivité s e = ni force magnétomotrice (A tt) f flux (W b) = 1 l m. S ( réluctance -1 A t. W b ) perméabilité induction magnétique (T) m j =s. E densité de courant -2 ( ) E e = Ri = ò Edl champ électrique -1 ( ) loi d'Ohm e = f = ò H dl champ magnétique -1 ( ) théorème d'Ampère i = òò jd. S conservation du courant f = òò Bd. S conservation du flux 6 A. m V. m B = m. H H A. m

Page 8 2. 1 - Circuits magnétiques Bobines à noyau de fer Un circuit magnétique est la partie ferromagnétique guidant le flux magnétique d ’un système électrique: Exemples: le noyau d ’un transformateur ou le corps d ’un moteur 7

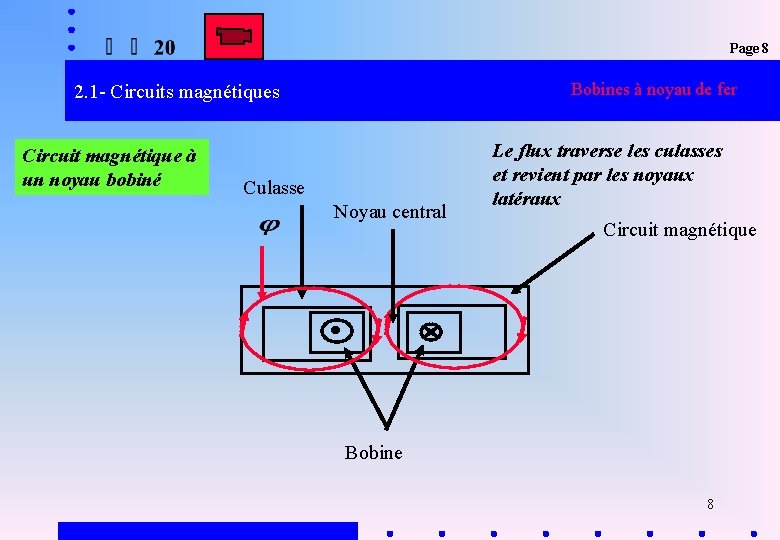
Page 8 Bobines à noyau de fer 2. 1 - Circuits magnétiques Circuit magnétique à un noyau bobiné Culasse Noyau central Le flux traverse les culasses et revient par les noyaux latéraux Circuit magnétique Bobine 8

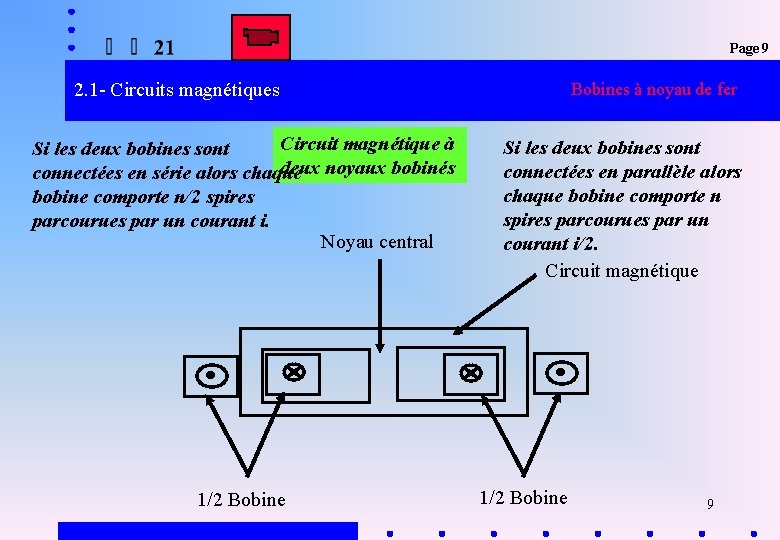
Page 9 2. 1 - Circuits magnétiques Circuit magnétique à Si les deux bobines sont deux noyaux bobinés connectées en série alors chaque bobine comporte n/2 spires parcourues par un courant i. Noyau central 1/2 Bobines à noyau de fer Si les deux bobines sont connectées en parallèle alors chaque bobine comporte n spires parcourues par un courant i/2. Circuit magnétique 1/2 Bobine 9

Page 9 2. 2 - Allure du courant absorbé Bobines à noyau de fer Pour obtenir l ’allure du courant absorbé i, on passe de v à B 10

Page 9 2. 2 - Allure du courant absorbé Bobines à noyau de fer Pour obtenir l ’allure du courant absorbé i, on passe de v à B et de B à H au moyen du cycle d ’hystérésis ou un tableau de B(H) De H on en déduit i L ’induction magnétique est sinusoïdale de valeur maximale La puissance active consommée par le circuit magnétique est appelée pertes fer. 11

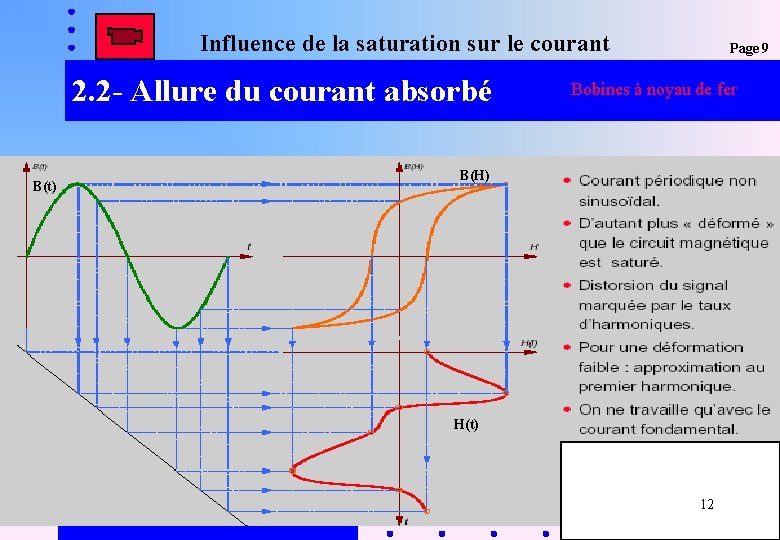
Influence de la saturation sur le courant 2. 2 - Allure du courant absorbé B(t) Page 9 Bobines à noyau de fer B(H) H(t) 12

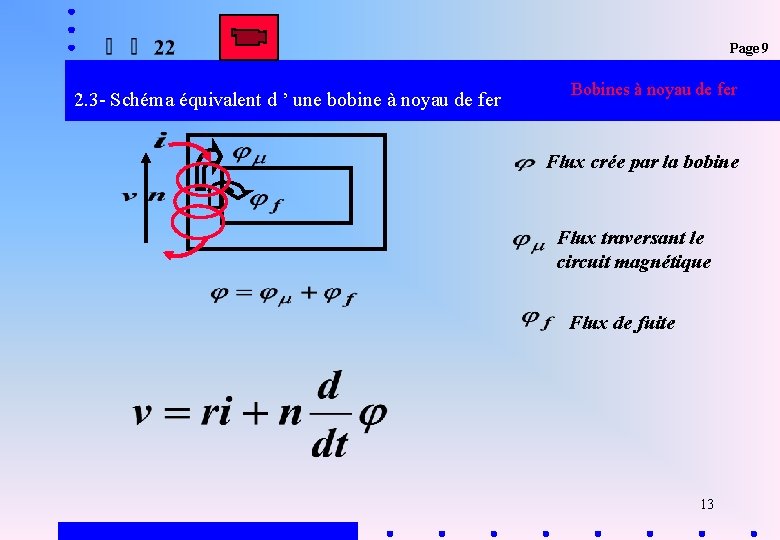
Page 9 2. 3 - Schéma équivalent d ’ une bobine à noyau de fer Bobines à noyau de fer Flux crée par la bobine Flux traversant le circuit magnétique Flux de fuite 13

Page 10 2. 3 - Schéma équivalent d ’ une bobine à noyau de fer Bobines à noyau de fer Le circuit magnétique est représenté par une réactance Les pertes fer sont représentés par une résistance 14

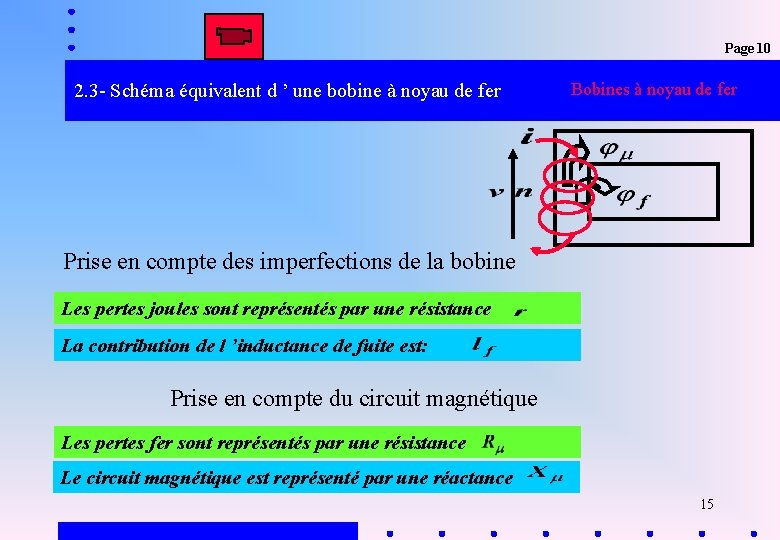
Page 10 2. 3 - Schéma équivalent d ’ une bobine à noyau de fer Bobines à noyau de fer Prise en compte des imperfections de la bobine Les pertes joules sont représentés par une résistance La contribution de l ’inductance de fuite est: Prise en compte du circuit magnétique Les pertes fer sont représentés par une résistance Le circuit magnétique est représenté par une réactance 15

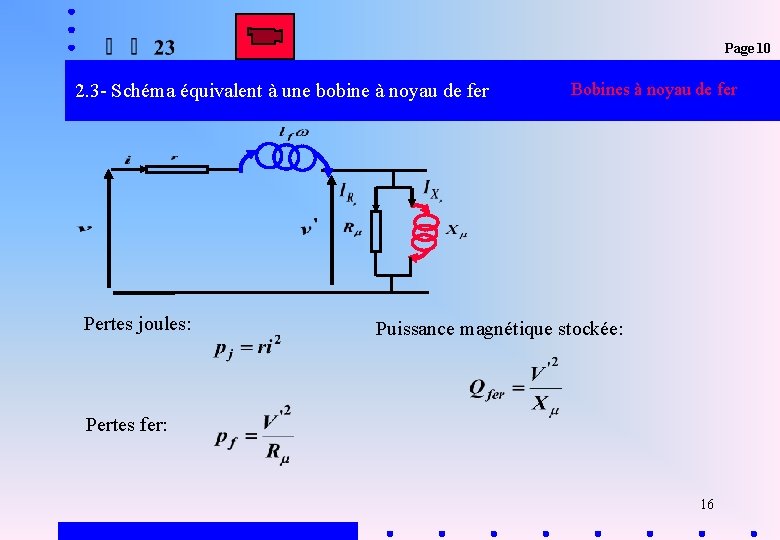
Page 10 2. 3 - Schéma équivalent à une bobine à noyau de fer Pertes joules: Bobines à noyau de fer Puissance magnétique stockée: Pertes fer: 16

Page 9 Pertes fer Bobines à noyau de fer 17

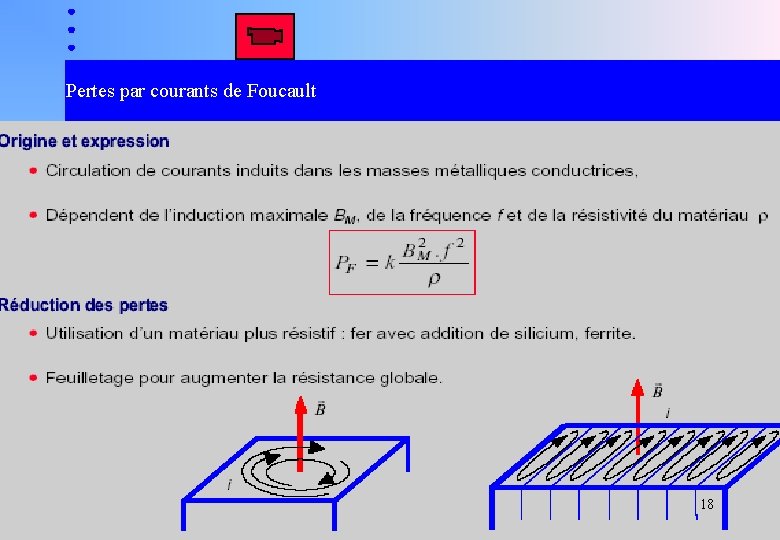
Pertes par courants de Foucault 18

Pertes par hystérésis Bobines à noyau de fer 19

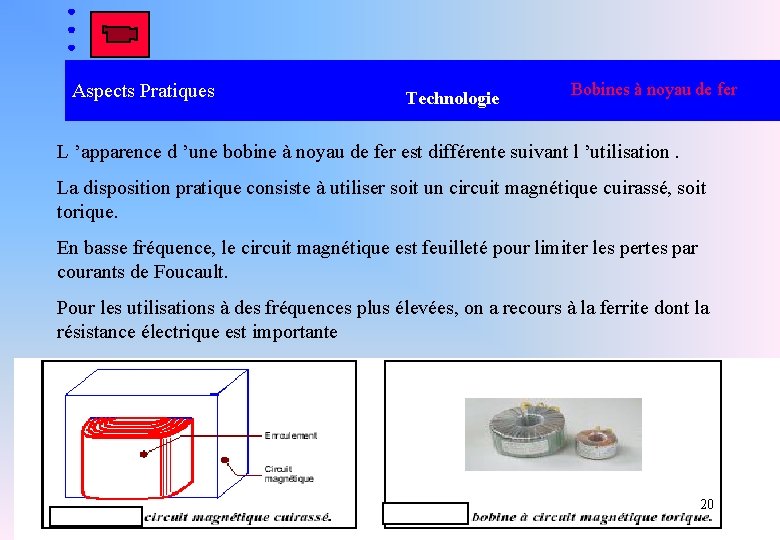
Aspects Pratiques Technologie Bobines à noyau de fer L ’apparence d ’une bobine à noyau de fer est différente suivant l ’utilisation. La disposition pratique consiste à utiliser soit un circuit magnétique cuirassé, soit torique. En basse fréquence, le circuit magnétique est feuilleté pour limiter les pertes par courants de Foucault. Pour les utilisations à des fréquences plus élevées, on a recours à la ferrite dont la résistance électrique est importante 20

Aspects Pratiques Application Bobines à noyau de fer En Électrotechnique, on rencontre les bobines à noyau de fer dans les électroaimants ( relais, contacteurs, levage ), les bobines d ’usage courant, les plateaux magnétiques de machines - outil ou les paliers magnétiques. En Électronique, on les trouvent dans les inductances de filtrage, les selfs HF ajustables ou non. Dans ces cas, les noyaux en ferrite sont de mise. 21

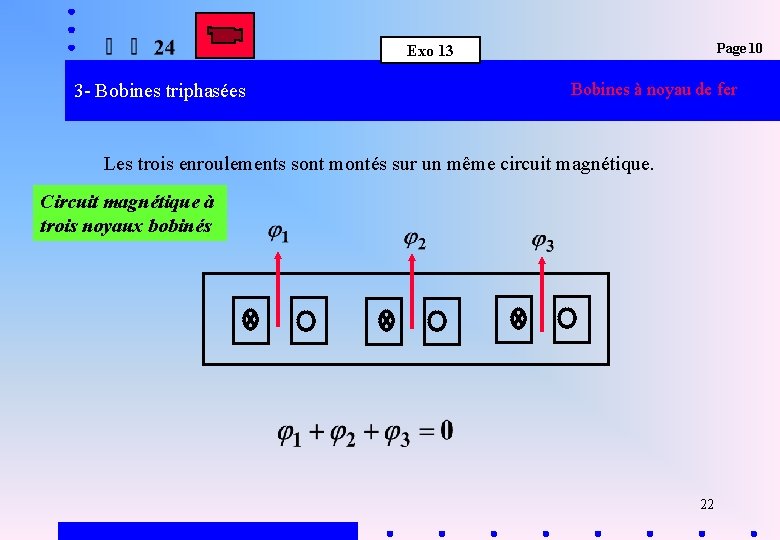
Page 10 Exo 13 3 - Bobines triphasées Bobines à noyau de fer Les trois enroulements sont montés sur un même circuit magnétique. Circuit magnétique à trois noyaux bobinés 22

Exo 13 Exercice 13 Calculez la réluctance du circuit magnétique ? Calculez l ’inductance de la bobine ? Calculez la valeur du courant i qui doit circuler dans la bobine? 23

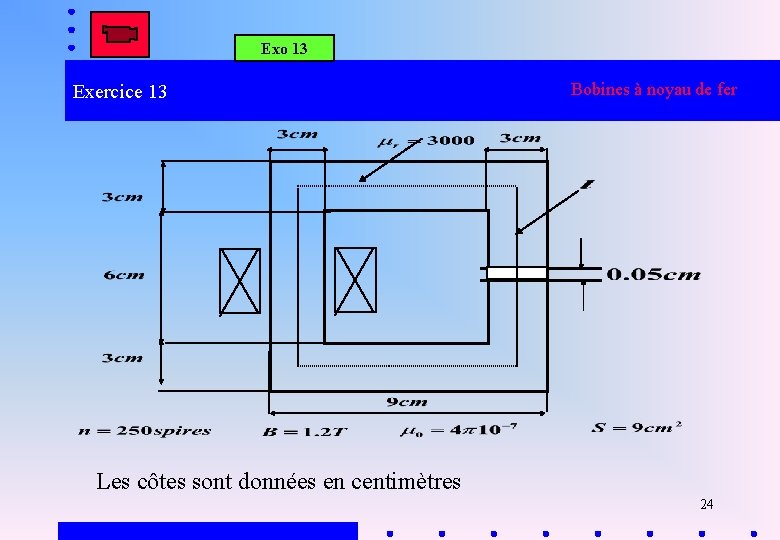
Exo 13 Exercice 13 Bobines à noyau de fer Les côtes sont données en centimètres 24

Exo 13 Exercice 13 Bobines à noyau de fer Réluctance du circuit magnétique Inductance de la bobine 25

Exo 13 Exercice 13 Bobines à noyau de fer Flux magnétique dans le noyau On a: Alors: 26

Exo 14 Page 10 Exercice 14 Calculez la valeur du courant i qui doit circuler dans la bobine? 27

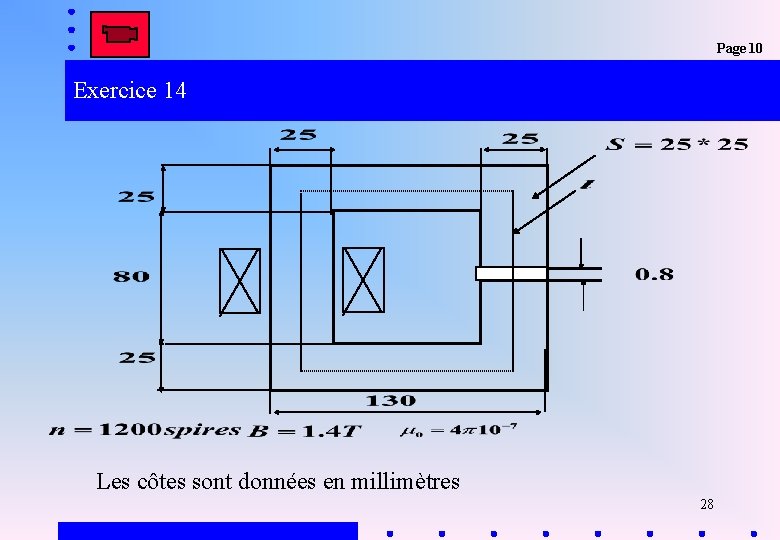
Page 10 Exercice 14 Les côtes sont données en millimètres 28

Page 10 Exercice 14 Flux magnétique dans le noyau et dans l ’entrefer Champs magnétique d ’excitation dans le fer H Voir courbe de B(H) Force magnétomotrice dans l ’entrefer Force magnétomotrice dans le fer (f. m. m)e = He*e (f. m. m)fer = H*l 29

Page 10 Exercice 14 f (wb ) S (m 2 ) entrefer 1. 4 * 25 * 10 - 6 fer 1. 4 * 25 * 10 -6 25 * 10 -6 -6 B(T ) H ( A / m) 1. 4 B 1. 4 m 0 = 1. 11 * 10 2450(tableau) f. m. m( AT ) l (m ) 6 0. 8 * 10 -3 (80 + 25) * 4 * 10 891 -3 1029 (f. m. m)total= 891+1029 = 1920 AT = n*i=1200*i 30

31