Coupling Water and Smoke to Thin Deformable and

Coupling Water and Smoke to Thin Deformable and Rigid Shells Eran Guendelman 1, 2 Andrew Selle 1, 3 Frank Losasso 1, 2 Ronald Fedkiw 1, 2 1 Stanford University, 2 Industrial Light + Magic, 3 Intel Corporation

Motivation • Fluid simulation becoming more common – Engineering, biomedicine, entertainment • Want interaction with thin solids – Parachutes – Cardiovascular simulation – CG characters w/clothing

Goal • Two-way coupling between: – Smoke or free-surface water – Thin rigid and deformable open shells • Prevent leaks across solid

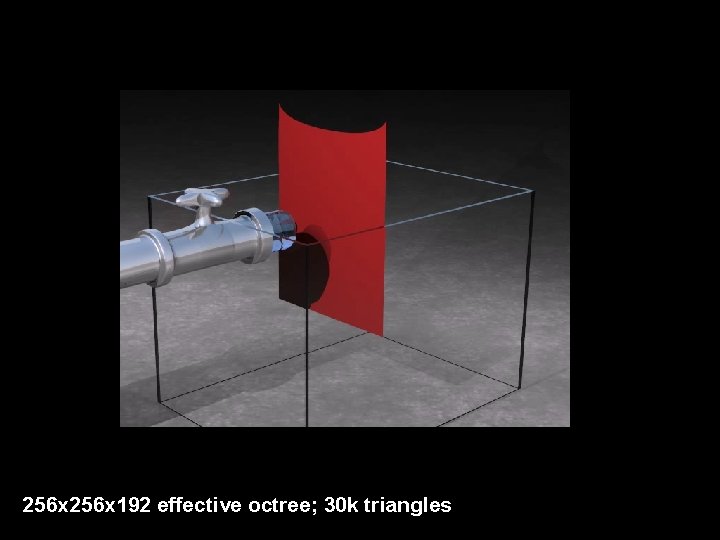
256 x 192 effective octree; 30 k triangles

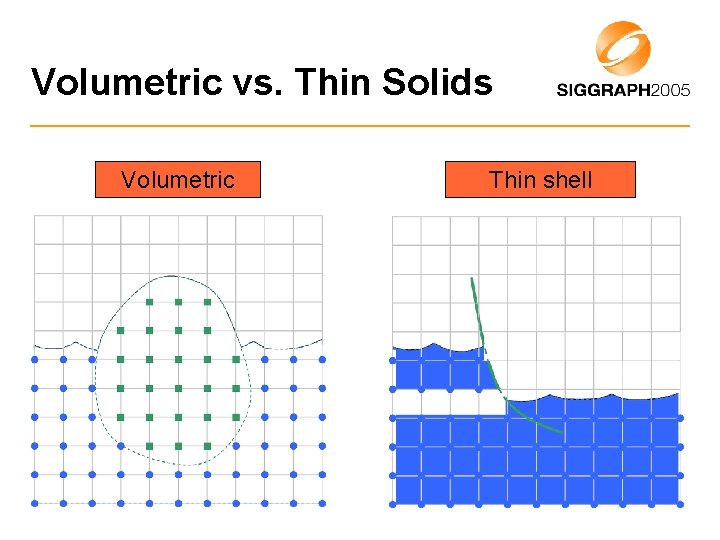
Volumetric vs. Thin Solids Volumetric Thin shell

Related Work: Volumetric • DLM / “Rigid Fluid” [Glowinski et al. ’ 94; Carlson et al. ’ 04] • Inter-particle forces [Génevaux et al. ’ 03; Müller et al. ’ 04] • Coupling solid velocity & fluid pressure – Incompressible: [Takahashi et al. ’ 02] – Compressible: [Yngve et al. ’ 00; Fedkiw ’ 02]

Diffuse Interface Methods • Smear solid onto fluid grid • e. g. Immersed boundary method [Peskin ‘ 72] – Parasitic currents

Sharp Interface Methods • Incorporate jump conditions into stencils – Ghost fluid method [Fedkiw et al. ’ 99; Tam et al. ‘ 05] – Immersed interface method [Le. Veque & Li ’ 94]

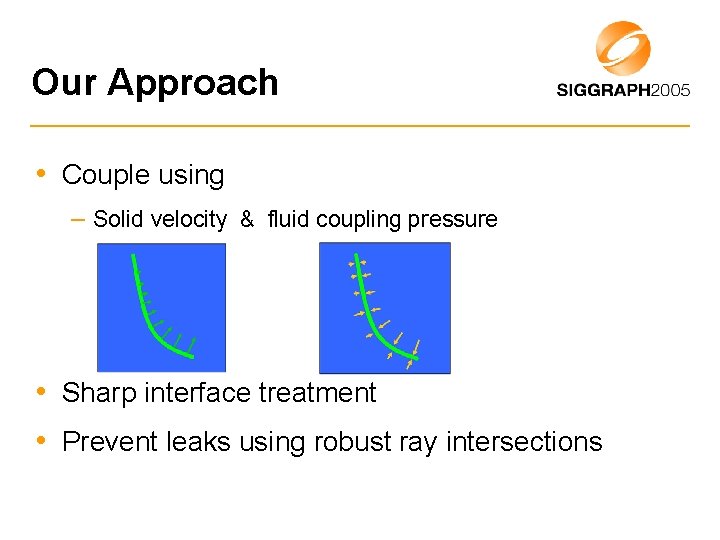
Our Approach • Couple using – Solid velocity & fluid coupling pressure • Sharp interface treatment • Prevent leaks using robust ray intersections

Talk Overview • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying coupling force • Summary and future work

Talk Overview • Fluid simulation (focus on water) • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Summary and future work

Fluid Simulation • Assume incompressible & inviscid • Use projection method: [Chorin ’ 68] un (u is fluid velocity) Advect un and add gravity ! u* u* violates incompressibility Project u* ! un+1 Compute pressure to enforce incompressibility un+1

Fluid Grid • Uniform & octree grids [Losasso et al. ’ 04] • Staggered grid configuration [Harlow & Welch ‘ 65]

Advection • First order semi-Lagrangian [Courant et al. ’ 52; Stam ‘ 99] – Advection on nodes

Particle Level Set Method [Enright et al. ‘ 02] • Level set captures water-air interface • Particles help correct interface water air

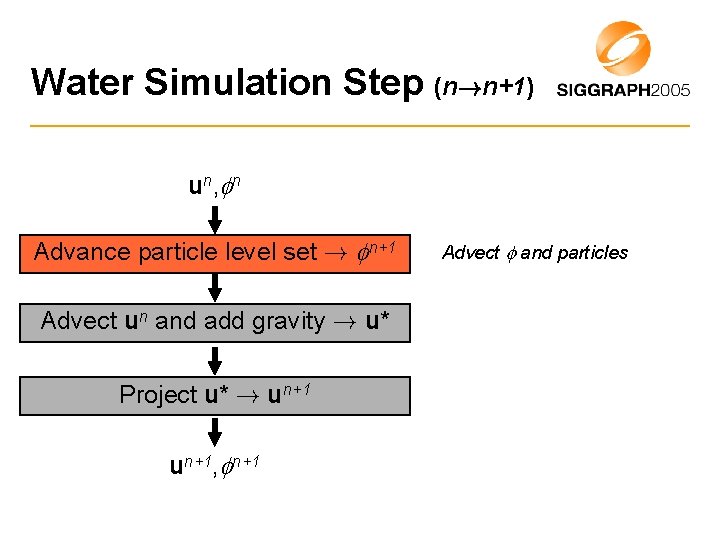
Water Simulation Step (n!n+1) u n, n Advance particle level set ! n+1 Advect un and add gravity ! u* Project u* ! un+1, n+1 Advect and particles

Now Add Solids to the Mix… • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Summary and future work

Now Add Solids to the Mix… • Black box: Input: external forces Output: positions and velocities [Guendelman et al. ’ 03] [Bridson et al. ’ 02, ’ 03]

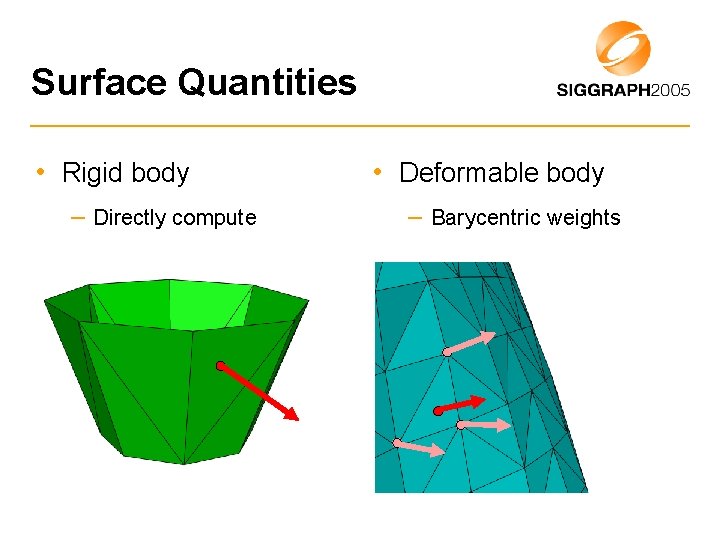
Surface Quantities • Rigid body – Directly compute • Deformable body – Barycentric weights

Talk Overview • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Examples, summary, and future work

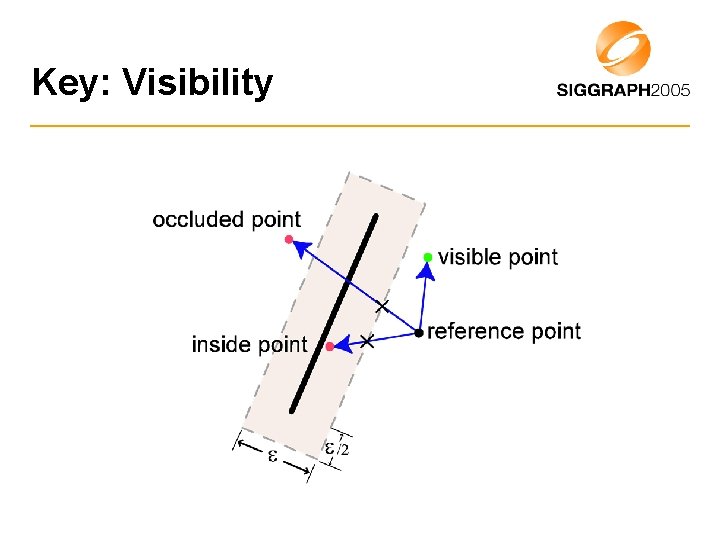
Key: Visibility

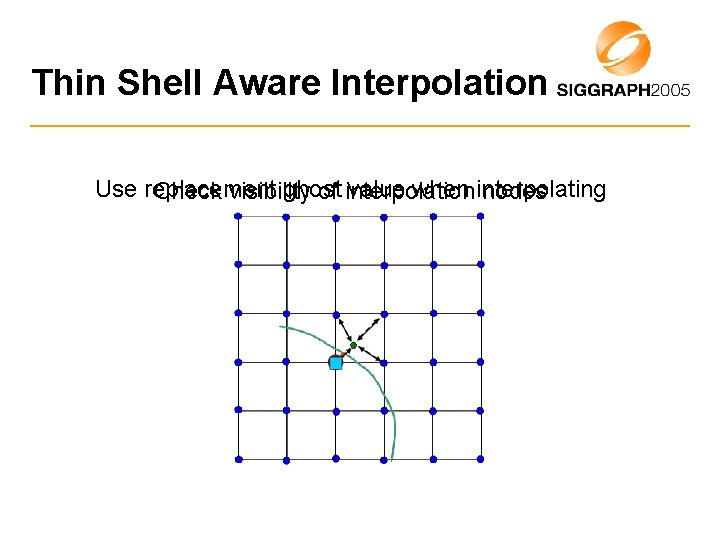
Thin Shell Aware Interpolation Use replacement ghost value when interpolating Check visibility of interpolation nodes

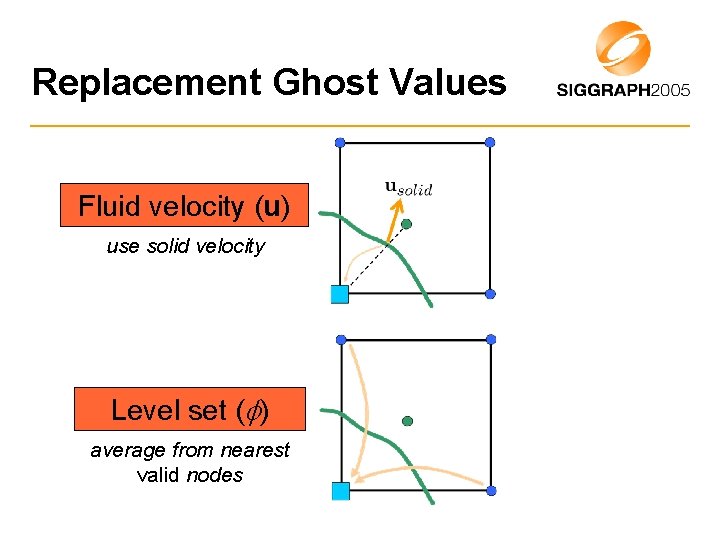
Replacement Ghost Values Fluid velocity (u) use solid velocity Level set ( ) average from nearest valid nodes

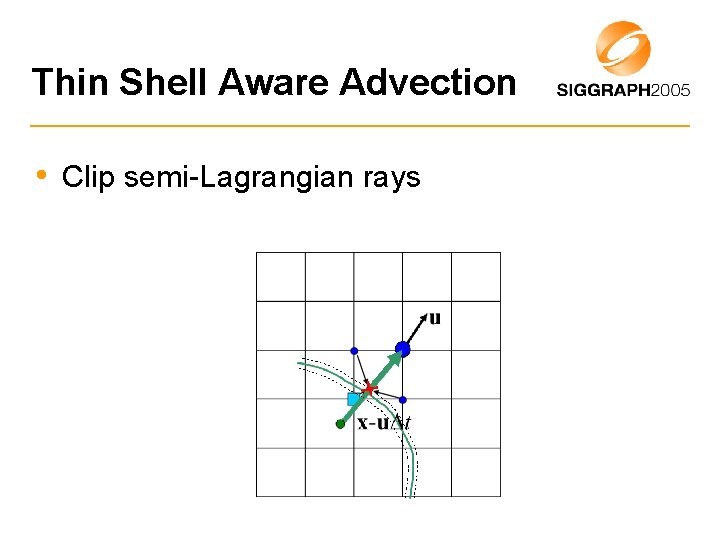
Thin Shell Aware Advection • Clip semi-Lagrangian rays

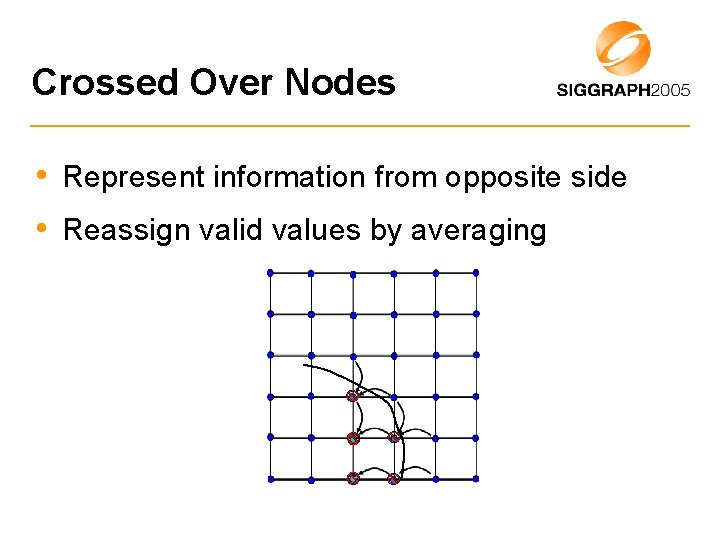
Crossed Over Nodes • Represent information from opposite side • Reassign valid values by averaging

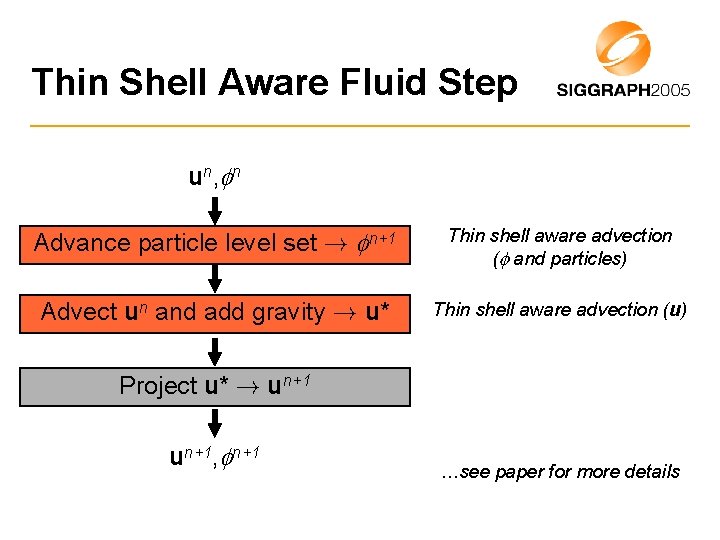
Thin Shell Aware Fluid Step u n, n Advance particle level set ! n+1 Thin shell aware advection ( and particles) Advect un and add gravity ! u* Thin shell aware advection (u) Project u* ! un+1, n+1 …see paper for more details

210 x 140 uniform; 30 k triangles

Talk Overview • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Summary and future work

Rasterizing Solid • Rasterize onto faces of fluid grid

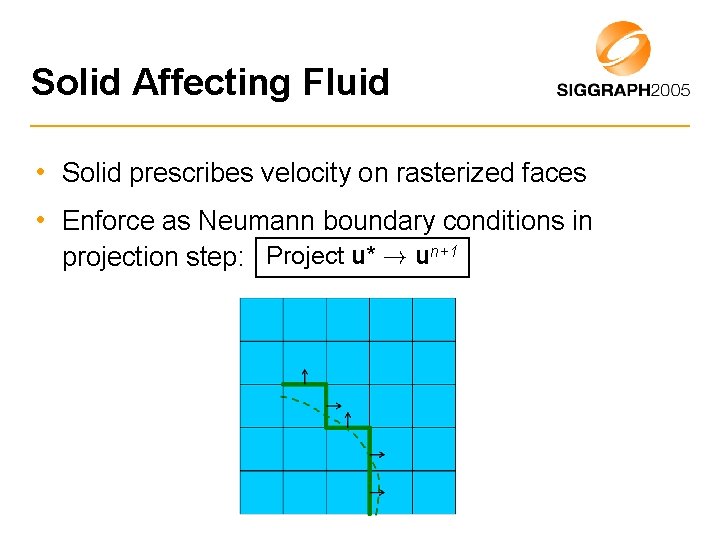
Solid Affecting Fluid • Solid prescribes velocity on rasterized faces • Enforce as Neumann boundary conditions in projection step: Project u* ! un+1

Which Solid Velocities? • At time n+1!n+2, at solid-fluid interface – Fluid moves with velocity enforced during un+1 projection – Solid moves from to Xn+1 to Xn+2 • Want these motions to match (reduce mass loss) • Solution: – Enforce effective solid velocity: Veff=(Xn+2 -Xn+1)/ t

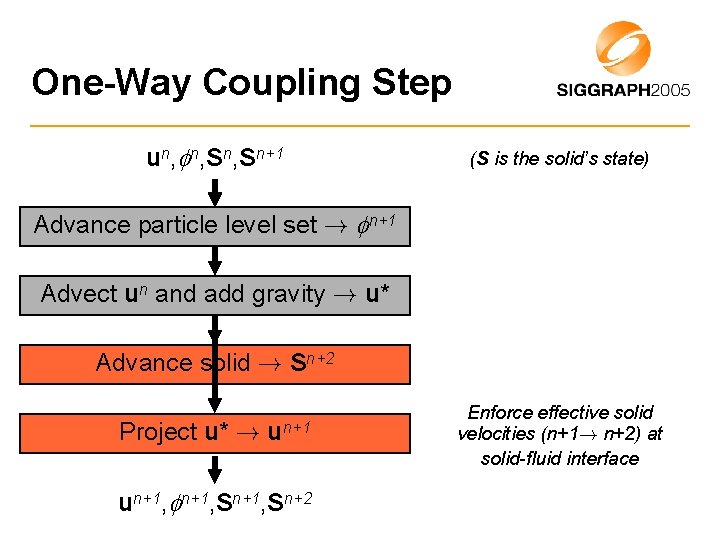
One-Way Coupling Step un, n, Sn+1 (S is the solid’s state) Advance particle level set ! n+1 Advect un and add gravity ! u* Advance solid ! Sn+2 Project u* ! un+1, Sn+2 Enforce effective solid velocities (n+1! n+2) at solid-fluid interface

160 x 192 x 160 effective octree

192 x 192 effective octree; 60 k triangles

Talk Overview • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Summary and future work

Fluid Coupling Force • Want to use fluid pressure • Incompressible pressure can be noisy – Incompressibility = hard constraint – Enforcing solid velocity = hard constraint – Better for compressible fluids [Yngve et al. ‘ 00; Fedkiw ‘ 02]

Smoother Coupling Pressure • Treat solid as fluid • Solve variable density fluid for pc • Similar to projection step, but: – Solid velocities not enforced – Fluid velocities not modified!

Two Pressure Solves! • Incompressible pressure (projection): – Enforce incompressibility & solid velocity – Essential for reducing mass loss • Coupling pressure: – Does not modify fluid velocity – Essential for smoother coupling force on solid

Must Enforce Solid Velocity Mass loss Rigid Fluid [Carlson et al. ’ 04] Enforcing solid velocity Enforced!

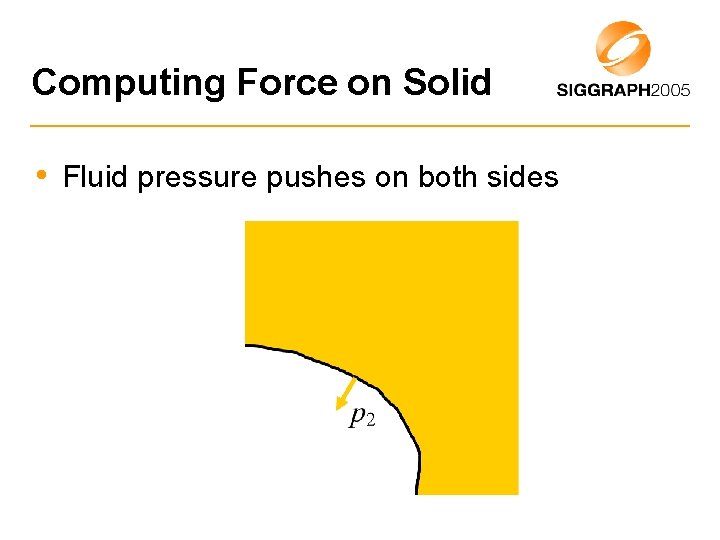
Computing Force on Solid • Fluid pressure pushes on both sides

Computing Force on Solid • Net force is proportional to pressure jump [pc]

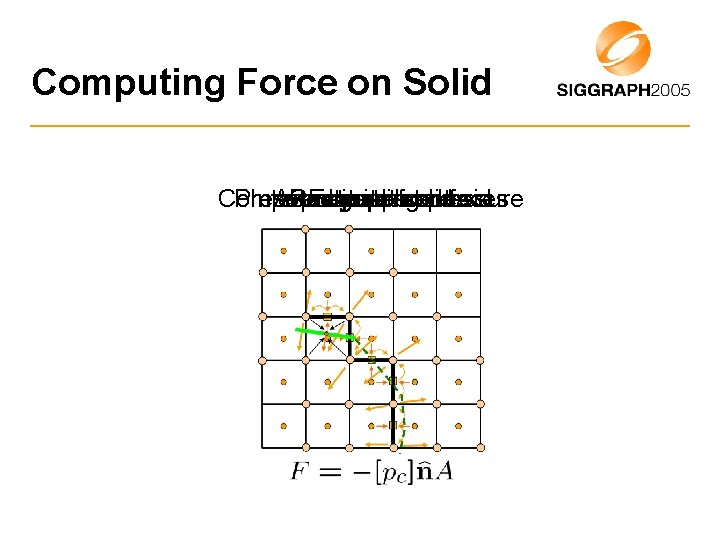
Computing Force on Solid Compute Interpolate Extrapolate at force centroid Average Rasterize to nodes solid Compute Pressure coupling jumps on pressure faces

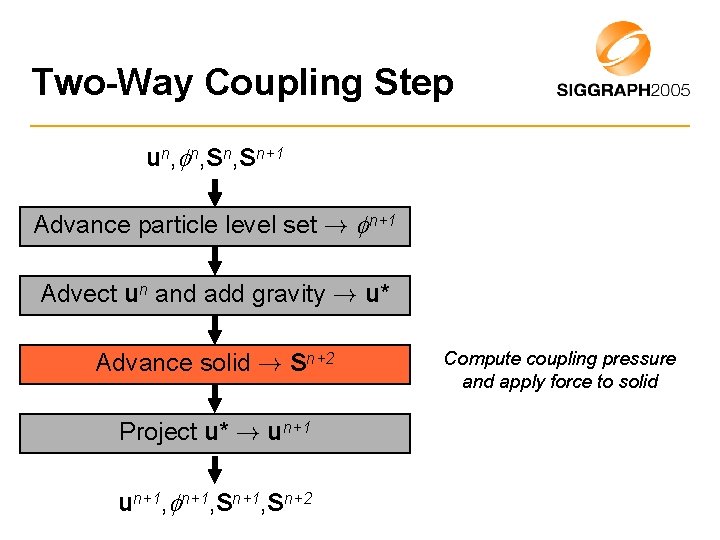
Two-Way Coupling Step un, n, Sn+1 Advance particle level set ! n+1 Advect un and add gravity ! u* Advance solid ! Sn+2 Project u* ! un+1, Sn+2 Compute coupling pressure and apply force to solid

148 x 111 uniform; 2. 5 k triangles

200 x 200 effective octree; 30 k triangles

256 x 192 effective octree; 30 k triangles

Talk Overview • Fluid simulation • Solid simulation • Preventing leaks across solid • Enforcing solid velocity on fluid • Computing and applying fluid coupling force • Summary and future work

Summary • Sharp interface treatment – Prevent leaks using ray intersections (visibility) • Solid prescribes velocity boundary conditions – Use effective velocity to reduce mass loss • Smooth coupling force applied to solid – Treat solid as fluid to compute smoother pressure

Future Work • Absorption, adhesion, permeability • Compare against experiments

Acknowledgements • Mike Houston, Christos Kozyrakis, Mark Horowitz, Bill Dally, Vijay Pande • Stanford Graphics Lab • ONR, ARO, NSF, PECASE, Sloan Foundation, Packard Foundation

The End