Coupled atomcavity system Rabi oscillation 2 level atom

Coupled atom-cavity system • Rabi oscillation: 2 -level atom in oscillating electromagnetic field i) stimulated emission |e, n> |G, n+1> ii) absorption |G, n+1> |e, n> • coupling energy: ћg = |Ď • Ē 0| , 2 g = frequency of Rabi cycle Energy dissipation rates: sources of decoherence κ = cavity decay rate (“leaking” energy) γ = free-space atomic dipole decay rate (spontaneous emission) Excited State Θ Credit: Caltech Quantum Optics Θ(t) = 2 gt Ground State

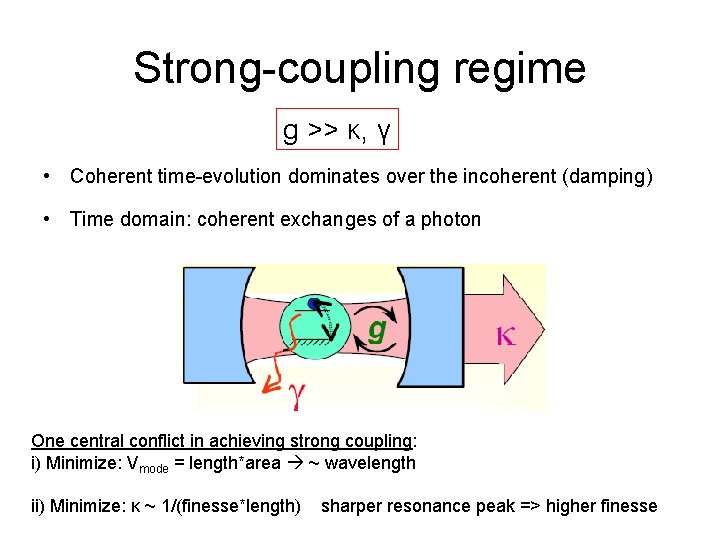
Strong-coupling regime g >> κ, γ • Coherent time-evolution dominates over the incoherent (damping) • Time domain: coherent exchanges of a photon One central conflict in achieving strong coupling: i) Minimize: Vmode = length*area ~ wavelength ii) Minimize: κ ~ 1/(finesse*length) sharper resonance peak => higher finesse

Another source of Decoherence Motional Effects: • coupling (g) depends on position of atom • Motional degrees of freedom • trapped ions could be useful in CQED • however, hard to fit ion trap in tiny optical-size cavity

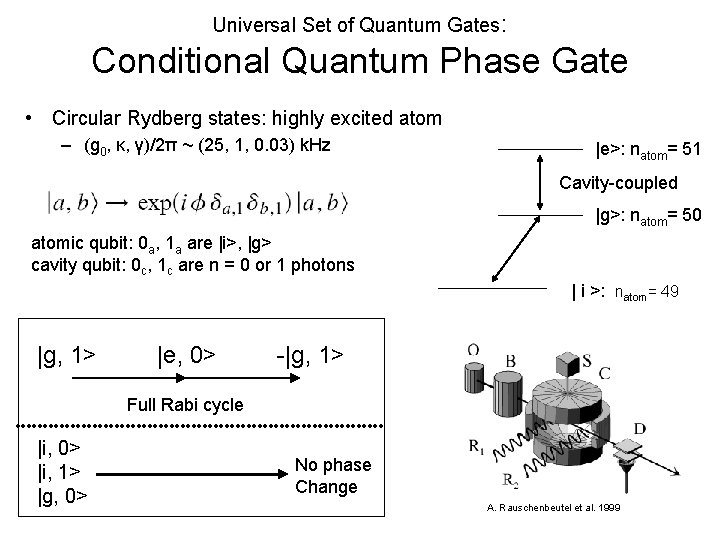
Universal Set of Quantum Gates: Conditional Quantum Phase Gate • Circular Rydberg states: highly excited atom – (g 0, κ, γ)/2π ~ (25, 1, 0. 03) k. Hz |e>: natom= 51 Cavity-coupled |g>: natom= 50 atomic qubit: 0 a, 1 a are |i>, |g> cavity qubit: 0 c, 1 c are n = 0 or 1 photons | i >: natom= 49 |g, 1> |e, 0> -|g, 1> Full Rabi cycle |i, 0> |i, 1> |g, 0> No phase Change A. Rauschenbeutel et al. 1999

Conditional Quantum Phase Gate for entanglement (average nphoton ~ 0. 18) Atomic qubit: Field qubit: Phase gate interaction => What good is entanglement in CQED? A. Rauschenbeutel et al. 1999