Counting Techniques Possibility Trees Multiplication Rule Permutations 1

Counting Techniques: Possibility Trees, Multiplication Rule, Permutations 1

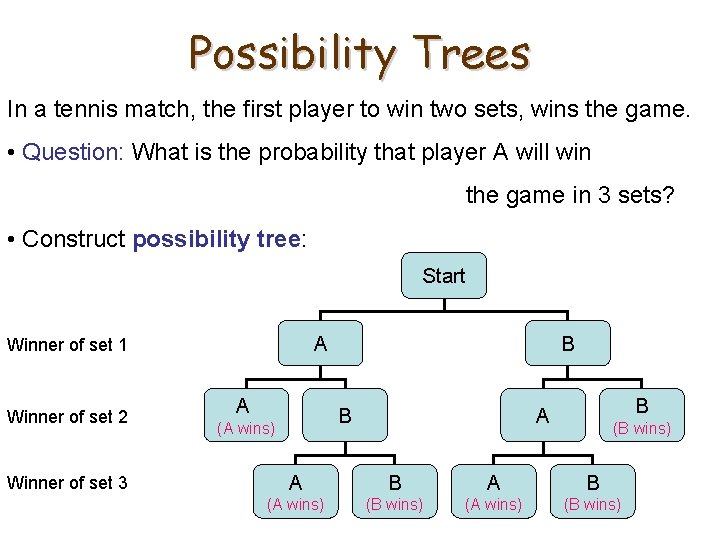
Possibility Trees In a tennis match, the first player to win two sets, wins the game. • Question: What is the probability that player A will win the game in 3 sets? • Construct possibility tree: Start A Winner of set 1 Winner of set 2 Winner of set 3 A B B (A wins) B A (B wins) A B (A wins) (B wins)

Possibility trees and Multiplication Rule Ø Example: When buying a PC system, you have the choice of 3 models of the basic unit: B 1, B 2, B 3 ; 2 models of keyboard: K 1, K 2 ; 2 models of printer: P 1, P 2. Ø Question: How many distinct systems can be purchased? 3

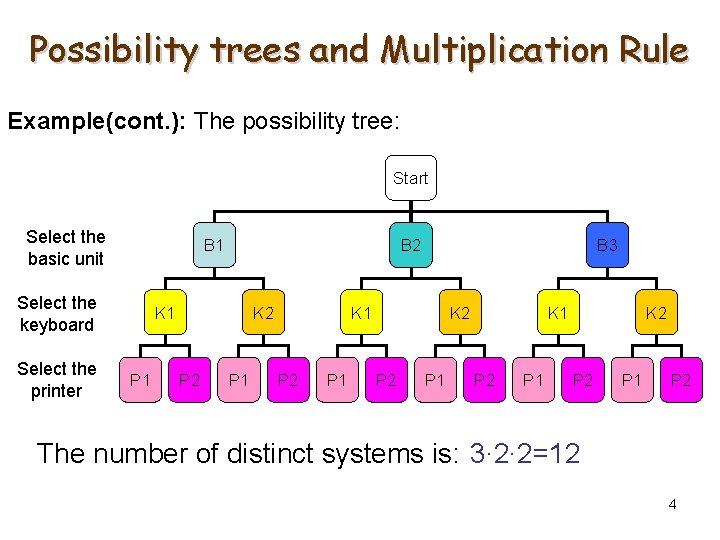
Possibility trees and Multiplication Rule Example(cont. ): The possibility tree: Start Select the basic unit B 1 Select the keyboard Select the printer B 2 K 1 P 1 K 2 P 1 B 3 K 1 P 2 P 1 K 2 K 1 P 2 P 1 P 2 The number of distinct systems is: 3∙ 2∙ 2=12 4

The Multiplication Rule If an operation consists of k steps and the 1 st step can be performed in n 1 ways, the 2 nd step can be performed in n 2 ways (regardless of how the 1 st step was performed) , …. the kth step can be performed in nk ways (regardless of how the preceding steps were performed) , then the entire operation can be performed in n 1 ∙ n 2 ∙… ∙ nk ways. 5

Multiplication Rule (Example) Ø Consider the following nested loop: for i: =1 to 5 for j: =1 to 6 [ Statement 1 ; Statement 2. ] next j next i Ø Question: How many times the statements in the inner loop will be executed? Ø Solution: 5 ∙ 6 = 30 times (based on the multiplication rule) 6

Multiplication Rule (Example) Ø A PIN is a sequence of any 4 digits (repetitions allowed); e. g. , 5279, 4346, 0270. Ø Question. How many different PINs are possible? Ø Solution. Choosing a PIN is a 4 -step operation: Step 1: Choose the 1 st symbol (10 different ways). Step 2: Choose the 2 nd symbol (10 different ways). Step 3: Choose the 3 rd symbol (10 different ways). Step 4: Choose the 4 th symbol (10 different ways). Based on the multiplication rule, 10∙ 10∙ 10 = 10, 000 PINs are possible.

Multiplication Rule (Example) Ø Consider the problem of choosing PINs but now repetitions are not allowed. Ø Question. How many different PINs are possible? Ø Solution. Choosing a PIN is a 4 -step operation: Step 1: Choose the 1 st symbol (10 different ways). Step 2: Choose the 2 nd symbol (9 different ways). Step 3: Choose the 3 rd symbol (8 different ways). Step 4: Choose the 4 th symbol (7 different ways). Based on the multiplication rule, 10∙ 9∙ 8∙ 7 = 5, 040 PINs are possible. 8

Multiplication Rule and Permutations Ø Consider the problem of choosing PINs again. Now a PIN is a sequence of 1, 2, 3, 4 ; repetitions are not allowed. Ø Question. How many different PINs are possible? Ø Solution. Choosing a PIN is a 4 -step operation: Step 1: Choose the 1 st symbol (4 different ways). Step 2: Choose the 2 nd symbol (3 different ways). Step 3: Choose the 3 rd symbol (2 different ways). Step 4: Choose the 4 th symbol (1 way). Based on the multiplication rule, 4∙ 3∙ 2∙ 1 = 4! = 24 PINs are possible. Ø Note: The number of different PINs in this case is just the number of different orders of 1, 2, 3, 4.

Permutations Ø A permutation of a set of objects is an ordering of the objects in a row. • Example: The permutations of {a, b, c}: abc acb bac bca cab cba Ø Theorem. For any integer n with n≥ 1, the number of permutations of a set with n elements is n!. Ø Proof. Forming a permutation is an n-step operation: Step 1: Choose the 1 st element ( n different ways). Step 2: Choose the 2 nd element ( n-1 different ways). … Step n: Choose the nth element (1 way). Based on the multiplication rule, the number of permutations is n∙(n-1)∙…∙ 2∙ 1 = n!

Example on Permutations: The Traveling Salesman Problem (TSP) Ø There are n cities. The salesman starts his tour from City 1, visits each of the cities exactly once, and returns to City 1. Question: How many different tours are possible? Answer: Each tour corresponds to a permutation of the remaining n-1 cities. Thus, the number of different tours is (n-1)!. Note: The actual goal of TSP is to find a minimum-cost tour. 11