COUNTING OUTCOMES TREE DIAGRAM A tree diagram is

TREE DIAGRAM A tree diagram is a picture of all the different ways that

TREE DIAGRAM You go out to breakfast one morning. You have the following choices

1. List the first choices given. Put some room in between them to draw

2. List each of the next choices for all the first choices you have.

3. Draw lines connecting each of the first choices to each of the second

4. Repeat steps 2 & 3 for each additional choice you have. Scrambled Pancakes

EXAMPLE Houses in the Heritage Hill district need to follow specific guidelines for the

White Brown Red Brick Green Blue Red White Tan Green White Brown Blue White

MULTIPLICATION COUNTING PRINCIPLE If there are m ways to make the first choice, and

Example You have 5 choices for meat toppings on a pizza, 6 vegatable choices,

Example How many 3 digit combinations are available on a combination lock if the

Example The Daily 3 Lottery game consists of choosing a 3 -digit number. How

Example How many different license plates can be made using 3 letters, then 3

Slides: 19

Download presentation

COUNTING OUTCOMES

TREE DIAGRAM A tree diagram is a picture of all the different ways that things can be combined.

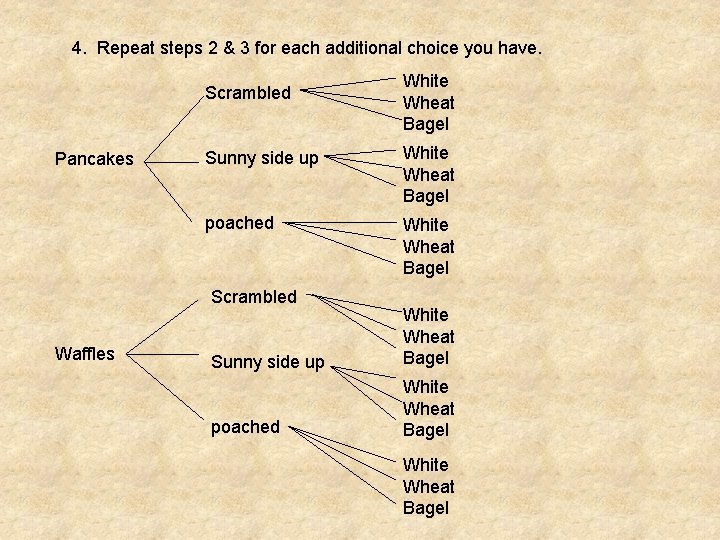
TREE DIAGRAM You go out to breakfast one morning. You have the following choices for your meal. You can choose either to have pancakes or waffles. You have three choices for eggs, scrambled, sunny side up, and poached. For choices of bread, you can have either white or wheat toast, or a bagel. Draw a tree diagram to show all the possible breakfast combinations you could have.

1. List the first choices given. Put some room in between them to draw the tree diagram. Pancakes Waffles

2. List each of the next choices for all the first choices you have. Pancakes Waffles

2. List each of the next choices for all the first choices you have. Scrambled Pancakes Sunny side up poached Waffles

2. List each of the next choices for all the first choices you have. Scrambled Pancakes Sunny side up poached Scrambled Waffles Sunny side up poached

3. Draw lines connecting each of the first choices to each of the second choices. Scrambled Pancakes Sunny side up poached Scrambled Waffles Sunny side up poached

4. Repeat steps 2 & 3 for each additional choice you have. Scrambled Pancakes Sunny side up White Wheat Bagel poached White Wheat Bagel Scrambled Waffles White Wheat Bagel Sunny side up White Wheat Bagel poached White Wheat Bagel

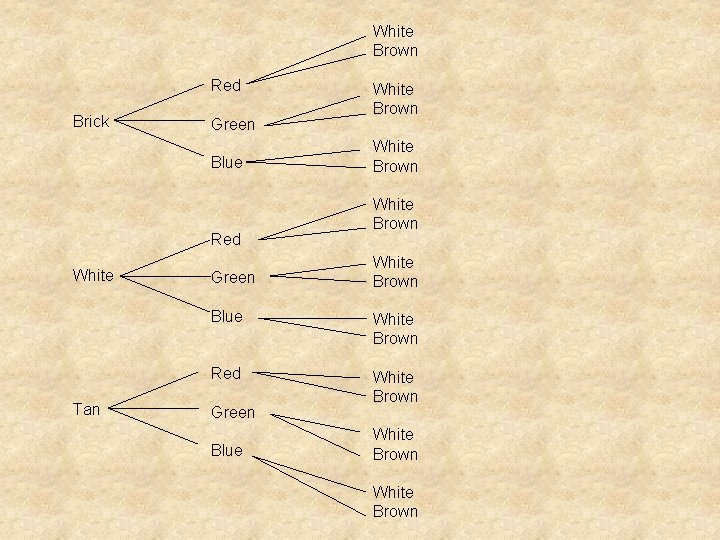
EXAMPLE Houses in the Heritage Hill district need to follow specific guidelines for the exterior finish on the house. The following are the choices a homeowner has: 1. The house can be brick, or have wood siding. If wood siding, the siding must be either white or tan. 2. The shutters must be either red, green, or blue. 3. The trim must be either white or brown. Draw a tree diagram showing all the possible combinations for the exterior of a house in this district.

White Brown Red Brick Green Blue Red White Tan Green White Brown Blue White Brown Red White Brown Green Blue White Brown

MULTIPLICATION COUNTING PRINCIPLE If there are m ways to make the first choice, and n ways to make the second choice, then there are (m)(n) ways to make both choices.

Example You have 5 choices for meat toppings on a pizza, 6 vegatable choices, and 3 cheese choices. How many possible combinations of pizza do you have?

Example You have 5 choices for meat toppings on a pizza, 6 vegatable choices, and 3 cheese choices. How many possible combinations of pizza do you have? So you could have 90 different pizzas.

Example How many 3 digit combinations are available on a combination lock if the dial is numbered from 0 - 49

Example The Daily 3 Lottery game consists of choosing a 3 -digit number. How many possible tickets are available?

Example How many different license plates can be made using 3 letters, then 3 numbers?

Assignment 12. 4 A: 1 – 4, 10, 11, 22