Counting Outcomes Counting Outcomes Objectives 1 To develop

Counting Outcomes

Counting Outcomes Objectives: (1) To develop fluency with counting strategies to determine the sample space for an event. Essential Questions: (1) How can I construct and use a frequency table (a. k. a. tree diagram)? (2) How can I use the Fundamental Counting Principle to find the number of outcomes?

Counting Outcomes (1) TREE DIAGRAMS A tree diagram is a diagram used to show the total number of possible outcomes in a probability experiment.

Counting Outcomes (2) THE FUNDAMENTAL COUNTING PRINCIPLE The Fundamental Counting Principle uses multiplication of the number of ways each event in an experiment can occur to find the number of possible outcomes in a sample space.

Counting Outcomes Example 1: Tree Diagrams. A new polo shirt is released in 4 different colors and 5 different sizes. How many different color and size combinations are available to the public? Colors – (Red, Blue, Green, Yellow) Styles – (S, M, L, XXL)
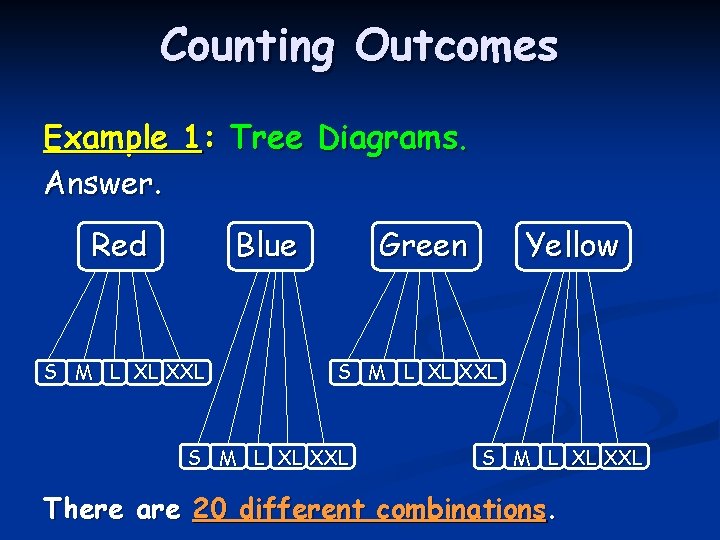
Counting Outcomes Example 1: Tree Diagrams. Answer. Red Blue S M L XL XXL Green Yellow S M L XL XXL There are 20 different combinations.

Counting Outcomes Example 1: The Fundamental Counting Principle. A new polo shirt is released in 4 different colors and 5 different sizes. How many different color and size combinations are available to the public? Colors – (Red, Blue, Green, Yellow) Styles – (S, M, L, XXL)

Counting Outcomes Example 1: The Fundamental Counting Principle. Answer. Number of Possible Styles 4 Number of Possible Sizes x 5 Number of Possible Comb. = 20

Counting Outcomes q Tree Diagrams and The Fundamental Counting Principle are two different algorithms for finding sample space of a probability problem. q However, tree diagrams work better for some problems and the fundamental counting principle works better for other problems.

Counting Outcomes Example 2: Tree Diagram. Tamara spins a spinner two times. What is her probability of spinning a green on the first spin and a blue on the second spin?

Counting Outcomes Example 2: Tree Diagram. Tamara spins a spinner two times. What is her probability of spinning a green on the first spin and a blue on the second spin? Green Blue Only one outcome has green then blue, and there are 4 possibilities…so the P(green, blue) = ¼ or. 25 or 25%

Counting Outcomes Guided Practice: Determine the probability for each problem. (1) How many outfits are possible from a pair of jean or khaki shorts and a choice of yellow, white, or blue shirt? (2) Scott has 5 shirts, 3 pairs of pants, and 4 pairs of socks. How many different outfits can Scott choose with a shirt, pair of pants, and pair of socks?

Counting Outcomes Guided Practice: Determine the probability for each problem. (1) Jean Shorts Yellow JSYS 1 White JSWS 2 (2) Number Of Shirts 5 Khaki Shorts Blue JSBS 3 Number Of Pants x 3 Yellow KSYS 4 White KSWS 5 Number Of Socks x 4 Blue KSBS 6 Number Of Outfits = 60

Counting Outcomes Real World Example: Tree Diagram. Kaitlyn tosses a coin 3 times. Draw a picture showing the possible outcomes. What is the probability of getting at least 2 tails?

Counting Outcomes Real World Example: Tree Diagram. Kaitlyn tosses a coin 3 times. Draw a picture showing the possible outcomes. What is the probability of getting at least 2 tails? Answer: P(at least 2 tails) = ½

Counting Outcomes Summary: - A tree diagram is used to show all of the possible outcomes, or sample space, in a probability experiment. - The fundamental counting principle can be used to count the number of possible outcomes given an event that can happen in some number of ways followed by another event that can happen in some number of different ways.

Counting Outcomes Summary: So when should I use a tree diagram or the fundamental counting principle? - A tree diagram is used to: (1) show sample space; (2) count the number of preferred outcomes. - The fundamental counting principle can be used to: (1) count the total number of outcomes.

Counting Outcomes Homework: -
- Slides: 18