Counting Models in Integer Domains Antonio Morgado Paulo

Counting Models in Integer Domains Ant’onio Morgado, Paulo Matos, Vasco Manquinho, and Jo˜ao Marques-Silva Presenter : Jen-Chi Lin 10/20/2021 1

Outline Abstract l Definitions l - ILP & PB - Model & Partial assignment - Convex polytope & Convex polyhedra Encoding ILP into Pseudo-Boolean l Encoding Pseudo-Boolean Constraints as SAT l - Counting Safety - Safe Encoding : BBR PB to SAT encoding 10/20/2021 2

Abstract l Problem : To count models in integer linear programming (ILP) using Boolean Satisfiability (SAT) techniques. l Approaches : (1) ILP → PB (Count in PB formulations) (2) ILP → PB → CNF (Count in CNF formulations) 10/20/2021 3

Definitions (1) l An Integer Linear Programming (ILP) problem : l An Pseudo-Boolean (PB, also known as 0 -1 ILP) problem : 10/20/2021 4

Definitions (2) l A propositional clause is a disjunction of literals such as where ＝ l Represented as linear inequalities : if we replace literals 10/20/2021 by 5

Definitions (3) l Model : Whenever an assignment to all problem variables is found such that all problem constraints become satisfied, we say that a model has been found. l Partial assignment : If not all problem variables are assigned to satisfy all problem constraints. → It represents a set of models for the problem instance. 10/20/2021 6

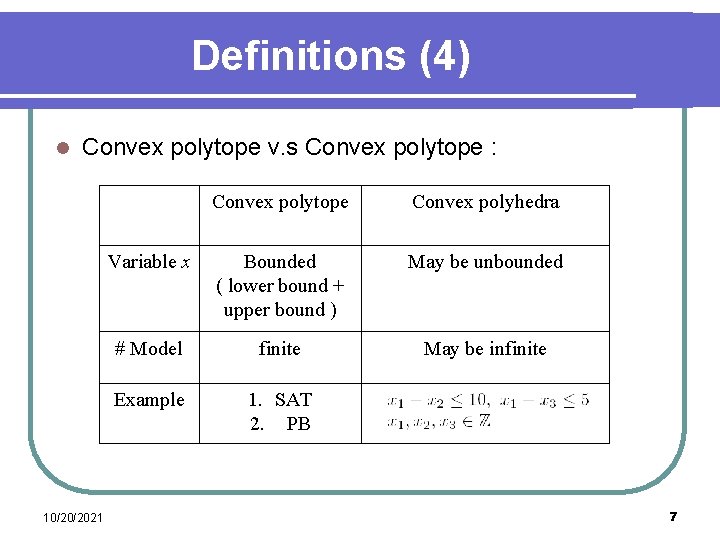
Definitions (4) l Convex polytope v. s Convex polytope : 10/20/2021 Convex polytope Convex polyhedra Variable x Bounded ( lower bound + upper bound ) May be unbounded # Model finite May be infinite Example 1. SAT 2. PB 7

Encoding ILP into Pseudo-Boolean (1) Assumption : The ILP instance defines a convex polytope. l Key : To determine lower and upper bounds on the possible values l of the integer valued variables in the ILP. → By solving a linear programming relaxation (LPR) : 10/20/2021 8

Encoding ILP into Pseudo-Boolean (2) l Let Since there’s no integer solution can be obtained such that → then 10/20/2021 9

Encoding ILP into Pseudo-Boolean (3) l Afterwards, is the number of bits necessary to represent l Additionally, we can also add the following constraints : l 10/20/2021 10

Encoding Pseudo-Boolean Constraints as SAT l Definition 1 (Counting Safety) A PB formulation to SAT encoding is counting safe iff the number of models in the PB formulation and in the encoded SAT formulation are the same. l Safe Encodings : (1) Warners PB to SAT encoding (2) Bailleux, Boufkhad and Roussel (BBR) PB to SAT encoding 10/20/2021 11

Encoding Pseudo-Boolean Constraints as SAT – BBR (1) l Consider a pseudo-Boolean constraint with the constraint literals sorted according to their coefficients : 10/20/2021 12

Encoding Pseudo-Boolean Constraints as SAT – BBR (2) l Introduce new Boolean variables s. t. l Terminal: 10/20/2021 13

Encoding Pseudo-Boolean Constraints as SAT – BBR (3) l The CNF encoding for a pseudo-Boolean constraint as follows : 10/20/2021 proceeds 14

Encoding Pseudo-Boolean Constraints as SAT – BBR (4) 10/20/2021 15

Encoding Pseudo-Boolean Constraints as SAT – BBR (5) 10/20/2021 16

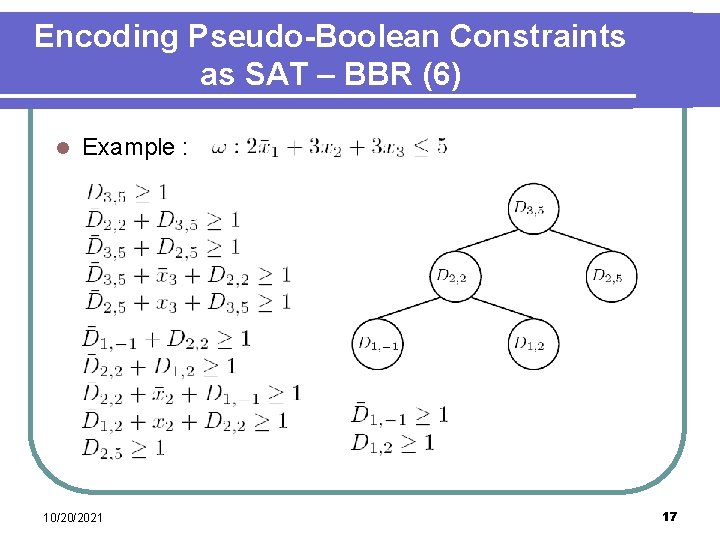
Encoding Pseudo-Boolean Constraints as SAT – BBR (6) l Example : 10/20/2021 17

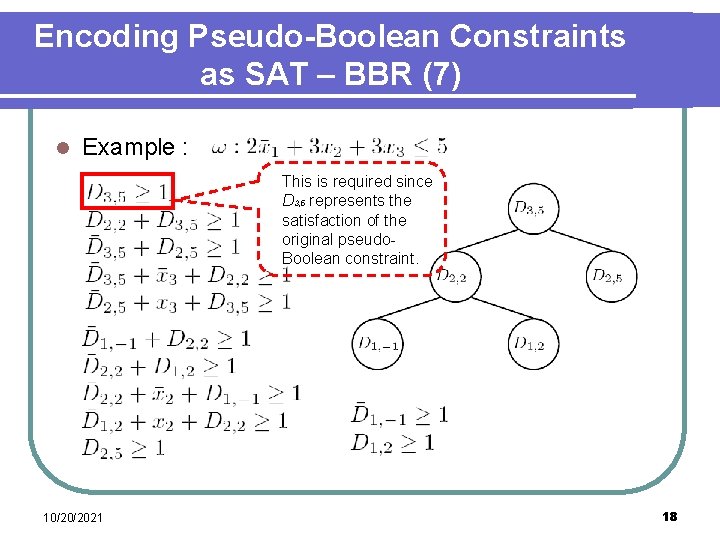
Encoding Pseudo-Boolean Constraints as SAT – BBR (7) l Example : This is required since D 3, 5 represents the satisfaction of the original pseudo. Boolean constraint. 10/20/2021 18

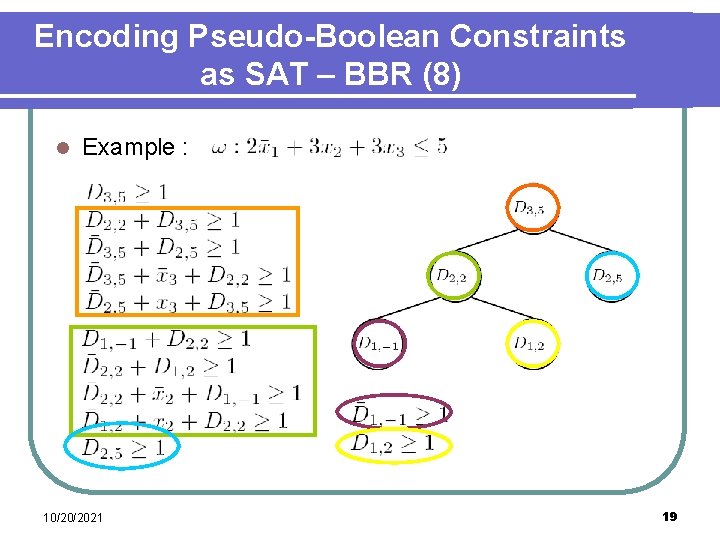
Encoding Pseudo-Boolean Constraints as SAT – BBR (8) l Example : 10/20/2021 19

Any question? 10/20/2021 20