Counting Elements of Disjoint Sets The Addition Rule

Example: Inclusion/Exclusion How many primes are there between 1 and 100? ¢ The non-primes

A Lemma ¢ Lemma: Let n and d be positive integers. There are n/d

Example: Inclusion/Exclusion Let A = {n | 1 n 100 and 2 divides n}.

Example: Inclusion/Exclusion ¢ By the Inclusion/Exclusion Rule, |A B C D| = |A| +

Example: Inclusion/Exclusion ¢ However, A B = {n | 1 n 100 and 6

Example: Inclusion/Exclusion ¢ Therefore, |A| = 100/2 = 50. l |A B| = 100/6

Example: Inclusion/Exclusion ¢ The number of multiples of 2, 3, 5, and 7 is

Example: Inclusion/Exclusion This count includes 2, 3, 5, 7, which are prime. ¢ This

Example: Inclusion/Exclusion ¢ How many integers from 1 to 1000 are multiples of 6,

Example: Inclusion/Exclusion ¢ ¢ ¢ ¢ |A| = 1000/6 = 166. |B| = 1000/10

Example: Inclusion/Exclusion ¢ How many 8 -bit numbers have either 1 in the 1

Slides: 12

Download presentation

Counting Elements of Disjoint Sets: The Addition Rule Lecture 27 Sections 6. 3 – 6. 4 Mon, Feb 28, 2005

Example: Inclusion/Exclusion How many primes are there between 1 and 100? ¢ The non-primes must be multiples of 2, 3, 5, or 7, since the square root of 100 is 10. ¢

A Lemma ¢ Lemma: Let n and d be positive integers. There are n/d multiples of d between 1 and n, where x represents the “floor” of x.

Example: Inclusion/Exclusion Let A = {n | 1 n 100 and 2 divides n}. ¢ Let B = {n | 1 n 100 and 3 divides n}. ¢ Let C = {n | 1 n 100 and 5 divides n}. ¢ Let D = {n | 1 n 100 and 7 divides n}. ¢

Example: Inclusion/Exclusion ¢ By the Inclusion/Exclusion Rule, |A B C D| = |A| + |B| + |C| + |D| – |A B| – |A C| – |A D| – |B C| – |B D| – |C D| + |A B C| – |A B C D|.

Example: Inclusion/Exclusion ¢ However, A B = {n | 1 n 100 and 6 | n}. l A B C = {n | 1 n 100 and 30 | n}. l B C D = {n | 1 n 100 and 105 | n}. l And so on. l

Example: Inclusion/Exclusion ¢ Therefore, |A| = 100/2 = 50. l |A B| = 100/6 = 16. l |A B C| = 100/30 = 3. l |B C D| = 100/105 = 0. l And so on. l

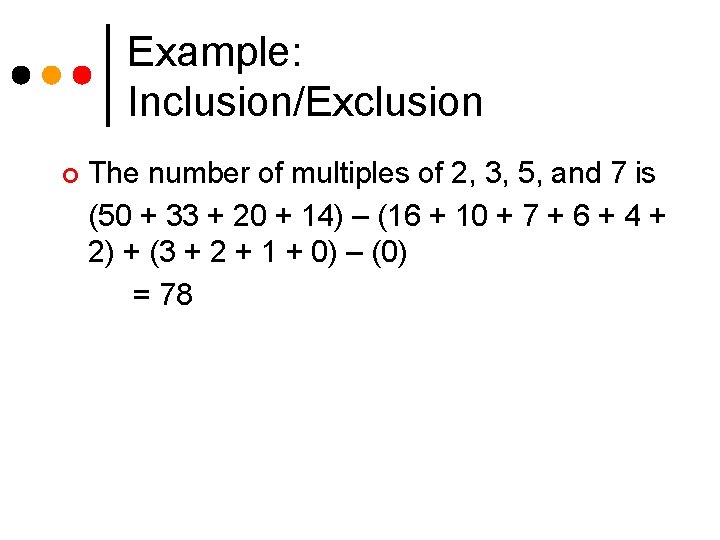
Example: Inclusion/Exclusion ¢ The number of multiples of 2, 3, 5, and 7 is (50 + 33 + 20 + 14) – (16 + 10 + 7 + 6 + 4 + 2) + (3 + 2 + 1 + 0) – (0) = 78

Example: Inclusion/Exclusion This count includes 2, 3, 5, 7, which are prime. ¢ This count does not include 1, which is not prime. ¢ Therefore, the number of primes is 100 – 78 + 4 – 1 = 25. ¢

Example: Inclusion/Exclusion ¢ How many integers from 1 to 1000 are multiples of 6, 10, or 15? Let A = {n | 1 n 100 and 6 divides n}. l Let B = {n | 1 n 100 and 10 divides n}. l Let C = {n | 1 n 100 and 15 divides n}. l What is A B? A C? B C? ¢ What is A B C? ¢

Example: Inclusion/Exclusion ¢ ¢ ¢ ¢ |A| = 1000/6 = 166. |B| = 1000/10 = 100. |C| = 1000/15 = 66. |A B| = 1000/30 = 33. |A C| = 1000/30 = 33. |B C| = 1000/30 = 33. |A B C| = 1000/30 = 33. Therefore, 266 numbers from 1 to 1000 are multiples of 6, 10, or 15.

Example: Inclusion/Exclusion ¢ How many 8 -bit numbers have either 1 in the 1 st and 2 nd positions, or l 0 in the 2 nd and 3 rd positions, or l 1 in the 3 rd and 4 th positions? l