Counter with Parallel Load Upcounter that can be
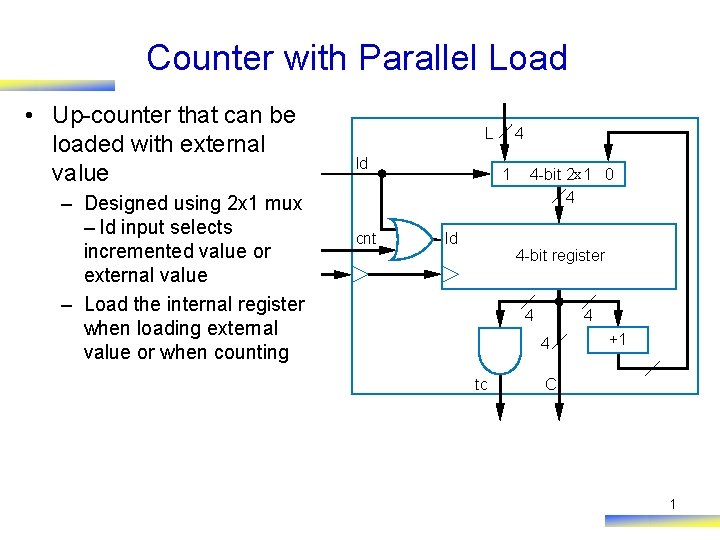
Counter with Parallel Load • Up-counter that can be loaded with external value – Designed using 2 x 1 mux – ld input selects incremented value or external value – Load the internal register when loading external value or when counting L ld cnt 4 1 ld 4 -bit 2 x 1 0 4 4 -bit register 4 4 4 tc +1 C 1
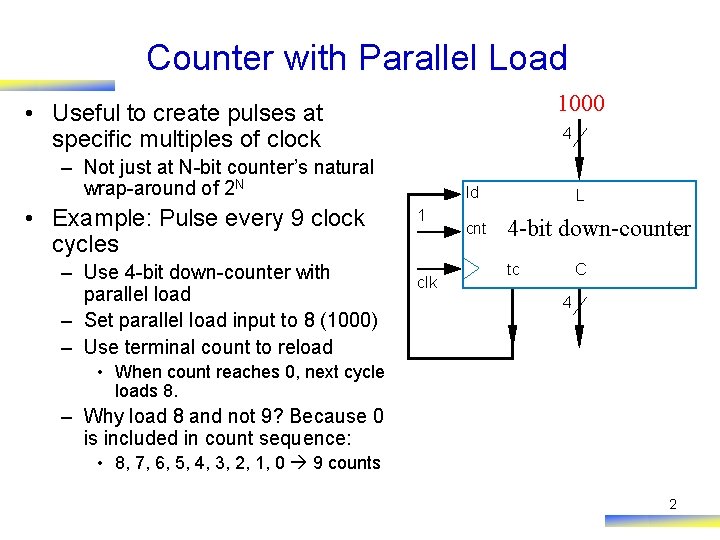
Counter with Parallel Load 1000 • Useful to create pulses at specific multiples of clock 4 – Not just at N-bit counter’s natural wrap-around of 2 N • Example: Pulse every 9 clock cycles – Use 4 -bit down-counter with parallel load – Set parallel load input to 8 (1000) – Use terminal count to reload ld 1 clk cnt L 4 -bit down-counter tc C 4 • When count reaches 0, next cycle loads 8. – Why load 8 and not 9? Because 0 is included in count sequence: • 8, 7, 6, 5, 4, 3, 2, 1, 0 9 counts 2
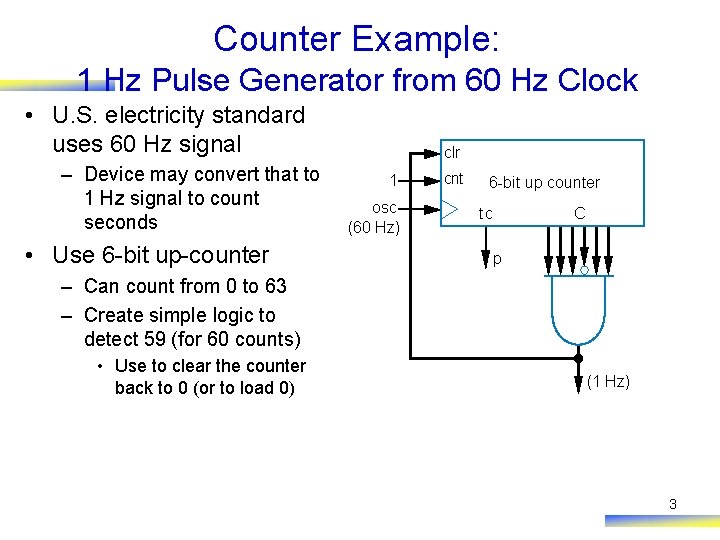
Counter Example: 1 Hz Pulse Generator from 60 Hz Clock • U. S. electricity standard uses 60 Hz signal – Device may convert that to 1 Hz signal to count seconds • Use 6 -bit up-counter clr 1 osc (60 Hz) cnt 6 -bit up counter tc C p – Can count from 0 to 63 – Create simple logic to detect 59 (for 60 counts) • Use to clear the counter back to 0 (or to load 0) (1 Hz) 3

Multiplier – Array Style • Can build multiplier that mimics multiplication by hand – Notice that multiplying multiplicand by 1 is same as ANDing with 1 4

Multiplier – Array Style • Generalized representation of multiplication by hand 5

Multiplier – Array Style • Multiplier design – array of AND gates a 3 a 2 a 1 a 0 pp 1 b 0 pp 2 b 1 0 b 2 0 pp 3 + (5 -bit) 00 A b 3 pp 4 + (6 -bit) 0 00 + (7 -bit) p 7. . p 0 * B P Block symbol 6
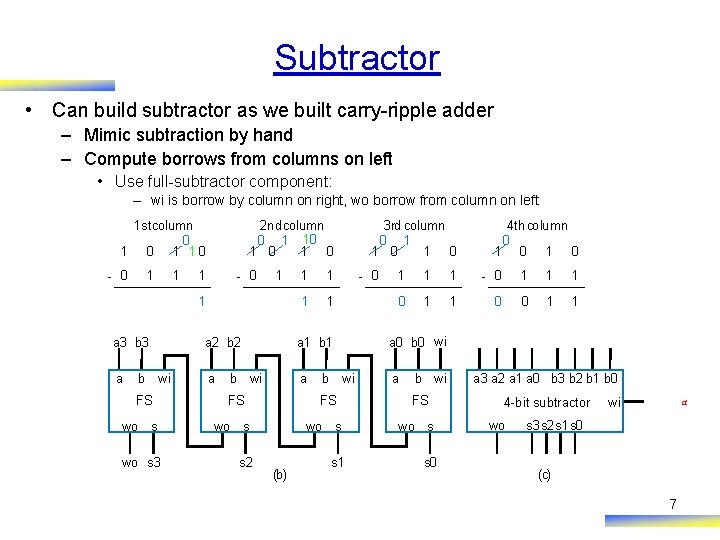
Subtractor • Can build subtractor as we built carry-ripple adder – Mimic subtraction by hand – Compute borrows from columns on left • Use full-subtractor component: – wi is borrow by column on right, wo borrow from column on left 1 stcolumn 0 1 10 - 0 1 1 2 nd column 0 1 10 1 0 - 0 1 1 1 1 3 rd column 0 1 1 0 - 0 1 1 1 0 0 1 1 a 3 b 3 a 2 b 2 a 1 b 1 a 0 b 0 wi a a b wi FS wo s 3 s 2 b wi FS (b) 4 th column 0 1 0 b wi FS wo s s 1 s 0 a 3 a 2 a 1 a 0 b 3 b 2 b 1 b 0 4 -bit subtractor wo wi a s 3 s 2 s 1 s 0 (c) 7

Subtractor Example: Color Space Converter – RGB to CMYK • Color – Often represented as weights of three colors: red, green, and blue (RGB) • Perhaps 8 bits each, so specific color is 24 bits – White: R=1111, G=1111, B=1111 – Black: R=0000, G=0000, B=0000 – Other colors: values in between, e. g. , R=00111111, G=0000, B=00001111 would be a reddish purple – Good for computer monitors, which mix red, green, and blue lights to form all colors • Printers use opposite color scheme – Because inks absorb light – Use complementary colors of RGB: Cyan (absorbs red), reflects green and blue, Magenta (absorbs green), and Yellow (absorbs blue) 8
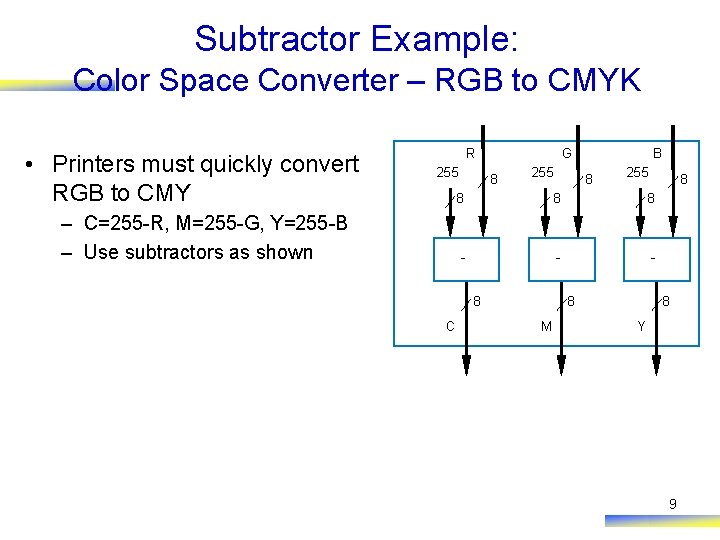
Subtractor Example: Color Space Converter – RGB to CMYK • Printers must quickly convert RGB to CMY R 255 – C=255 -R, M=255 -G, Y=255 -B – Use subtractors as shown G 8 255 8 8 - - - 8 C B 8 M 8 Y 9

Subtractor Example: Color Space Converter – RGB to CMYK • Try to save colored inks – Expensive – Imperfect – mixing C, M, Y doesn’t yield good-looking black • Solution: Factor out the black or gray from the color, print that part using black ink – e. g. , CMY of (250, 200)= (200, 200) + (50, 0, 0). • (200, 200) is a dark gray – use black ink 10
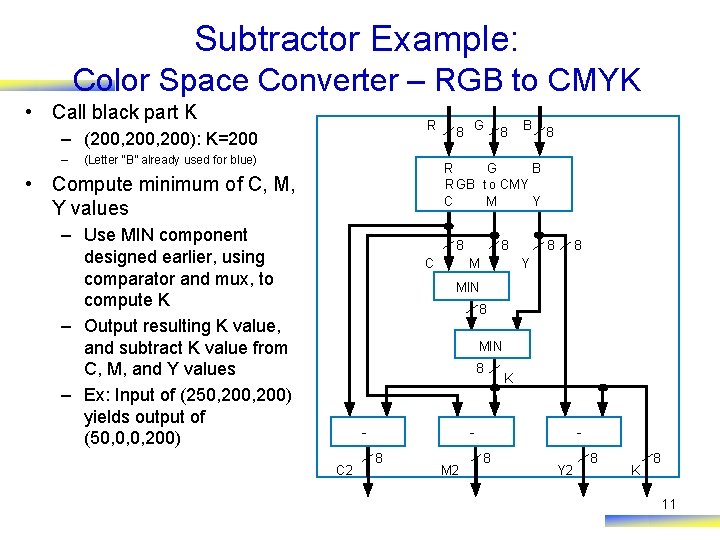
Subtractor Example: Color Space Converter – RGB to CMYK • Call black part K R – (200, 200): K=200 – (Letter “B” already used for blue) 8 G 8 B 8 R G B RGB t o CMY C M Y • Compute minimum of C, M, Y values – Use MIN component designed earlier, using comparator and mux, to compute K – Output resulting K value, and subtract K value from C, M, and Y values – Ex: Input of (250, 200) yields output of (50, 0, 0, 200) 8 C 8 M 8 8 Y MIN 8 C 2 K 8 M 2 8 Y 2 8 K 8 11

Representing Negative Numbers: Two’s Complement • Negative numbers common – How represent in binary? • Signed-magnitude – Use leftmost bit for sign bit • So -5 would be: 1101 using four bits 10000101 using eight bits • Better way: Two’s complement – Big advantage: Allows us to perform subtraction using addition – Thus, only need adder component, no need for separate subtractor component! 12

Ten’s Complement • Before introducing two’s complement, let’s consider ten’s complement – But, be aware that computers DO NOT USE TEN’S COMPLEMENT. Introduced for intuition only. – Complements for each base ten number shown to right – Complement is the number that when added results in 10 1 9 2 8 3 7 4 6 5 5 6 4 7 3 8 2 9 1 13

Ten’s Complement • Nice feature of ten’s complement – Instead of subtracting a number, adding its complement results in answer exactly 10 too much – So just drop the 1 – results in subtracting using addition only - 14

Two’s Complement is Easy to Compute: Just Invert Bits and Add 1 • Hold on! – Sure, adding the ten’s complement achieves subtraction using addition only – But don’t we have to perform subtraction to have determined the complement in the first place? e. g. , we only know that the complement of 4 is 6 by subtracting 10 -4=6 in the first place. • True – but in binary, it turns out that the two’s complement can be computed easily – – Two’s complement of 011 is 101, because 011 + 101 is 1000 Could compute complement of 011 as 1000 – 011 = 101 Easier method: Just invert all the bits, and add 1 The complement of 011 is 100+1 = 101 -- it works! Q: What is the two’s complement of 0101? A: 1010+1=1011 a (check: 0101+1011=10000) Q: What is the two’s complement of 0011? A: 1100+1=1101 15
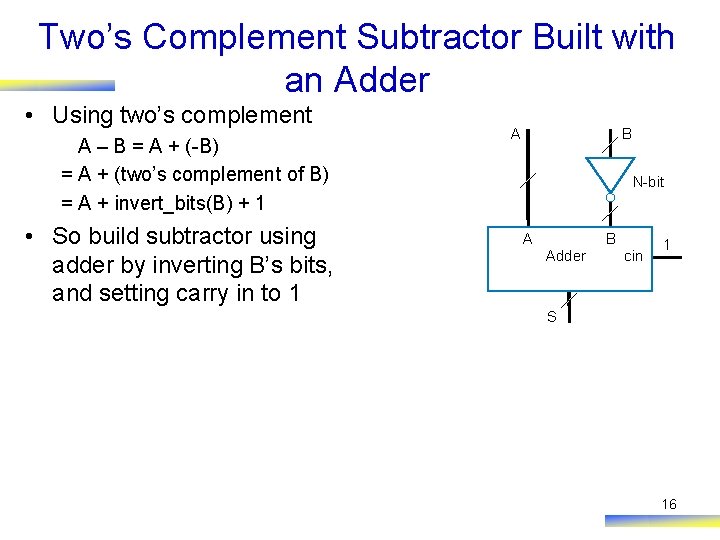
Two’s Complement Subtractor Built with an Adder • Using two’s complement A – B = A + (-B) = A + (two’s complement of B) = A + invert_bits(B) + 1 • So build subtractor using adder by inverting B’s bits, and setting carry in to 1 A B N-bit A B Adder cin 1 S 16

Arithmetic-Logic Unit: ALU • ALU: Component that can perform any of various arithmetic (add, subtract, increment, etc. ) and logic (AND, OR, etc. ) operations, based on control inputs • Motivation: – Suppose want multifunction calculator that not only adds and subtracts, but also increments, ANDs, ORs, XORs, etc. 17
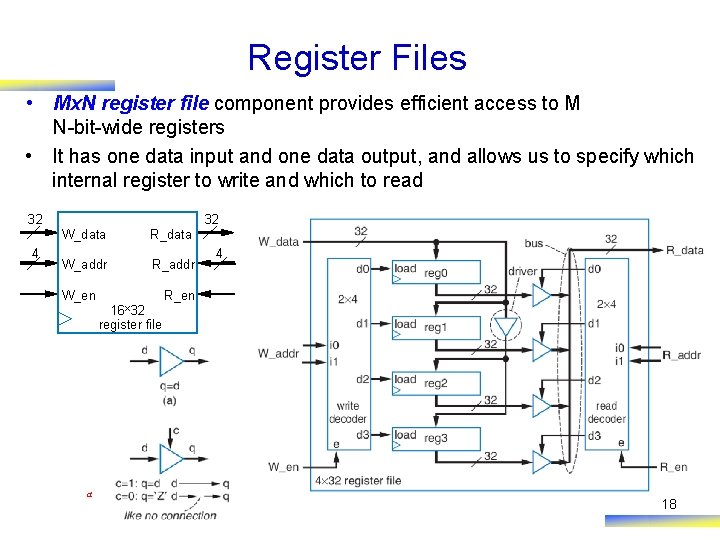
Register Files • Mx. N register file component provides efficient access to M N-bit-wide registers • It has one data input and one data output, and allows us to specify which internal register to write and which to read 32 4 32 W_data R_data W_addr R_addr W_en a 16× 32 register file a 4 R_en 18
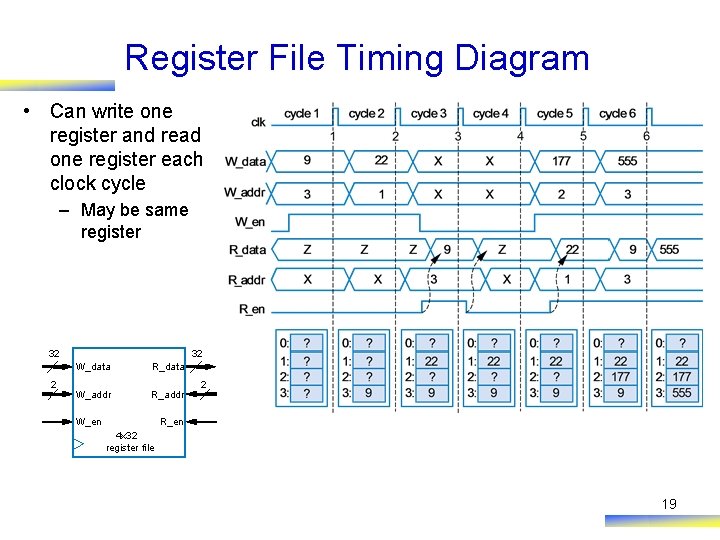
Register File Timing Diagram • Can write one register and read one register each clock cycle – May be same register 32 2 32 W_data R_data W_addr R_addr W_en 2 R_en 4 x 32 register file 19
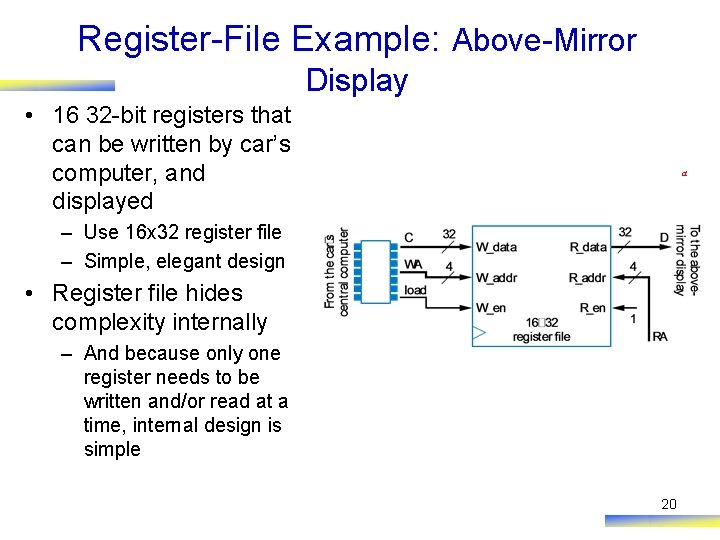
Register-File Example: Above-Mirror Display • 16 32 -bit registers that can be written by car’s computer, and displayed 32 a d 0 4× 16 – Use 16 x 32 register file – Simple, elegant design 4 • Register file hides complexity internally – And because only one register needs to be written and/or read at a time, internal design is simple OLD design C load reg 0 huge mux 32 too much fanout i 0 32 -bit 16 x 1 i 3 -i 0 d 32 congestion e load d 15 load reg 15 32 i 15 s 3 -s 0 20 D
- Slides: 20