COT 6930 HPC and Bioinformatics Multiple Sequence Alignment

COT 6930 HPC and Bioinformatics Multiple Sequence Alignment Xingquan Zhu Dept. of Computer Science and Engineering

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

What is a Multiple Sequence Alignment? l l l Pairwise alignments: involve two sequences Multiple sequence alignments: involve more than 2 sequences (often 100’s, either nucleotide or protein). A formal definition l l Hs Sp Tg Pf A multiple alignment of strings S 1, … Sk is a series of strings with spaces such that |S 1’| = … = |Sk’| Sj’ is an extension of Sj by insertion of spaces Goal: Find an optimal multiple alignment. ---MK-------MKKFQLF MTAAKKLSLF ----MN --LSLVAAML SILSYFVALF SLAALFCLLS QIRPYILLLI LLLSAARAEE LLPMAFASGD VATLRPVAAS VSLLKFISAV EDKK-EDVGT DNST-ESYGT DAEEGKVKDV DSN---IEGP VVGIDLGTTY VIGIDLGTTY

Why we do multiple alignments? l l In order to reveal the relationship between a group of sequences (homology) Simultaneous alignment of similar gene sequences may l l Discover the conserved regions in genes Determine the consensus sequence of these aligned sequences Help defines a protein family that may share a common biochemical function or evolutionary origin and thus reveals an evolutionary history of the sequences. Help prediction of the secondary and tertiary structures of new sequences

MSA Methods l Multidimensional dynamic programming l l Star Alignment, Tree Alignment, Progressive Alignment l l Extension of DP to multiple (3) sequences Starting with an alignment of the most alike sequences and building an alignment by adding more sequences Iterative methods l Making an initial alignment of groups of sequences and revising the alignment to achieve a more reasonable result

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

Multiple Sequence Alignment by DP l Pairwise sequence alignment l l Extension to 3 sequences l l a scoring matrix where each position provides the best alignment up to that point the lattice of a cube that is to be filled with calculated dynamic programming scores. Scoring positions l on 3 surfaces of the cube represent the alignment of a pair

Scoring of MSA: Sum of Pairs l Scores = summation of all possible combinations of amino acid pairs l - I K S S E l Using BLOSUM 62 matrix, gap penalty -8 In column 1, we have pairs l l l -8 - 8 + 4 = -12 l -, S S, S k(k-1)/2 pairs per column

Sum of Pairs l Given 5 sequences: NCCE NNCE N - CN SC SE l How many possible combinations of pairwise alignments for each position?

Sum of Pairs Assume: match/mismatch/gap = 1/0/-1 N C C E N N C E N - C N S C S E The 1 st position: # of N-N (3), # of S-S (1), # of N-S (6) SP(1) = 4*1 + 0*6 + (-1)*0 = 4 The 2 nd position: # of C-C (3), # of N-C (3), # of gaps (4), SP(2) = 3*1 + 0*3 + (-1)*4 = -1 l

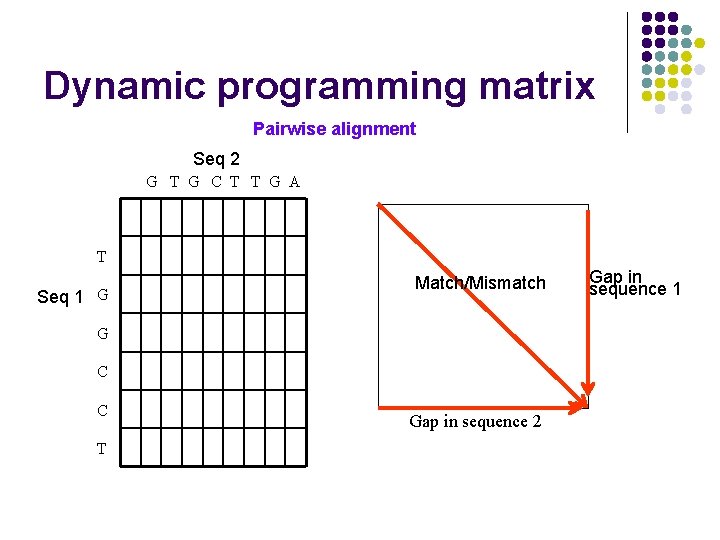
Dynamic programming matrix Pairwise alignment Seq 2 G T G C T T G A T Seq 1 G Match/Mismatch G C C T Gap in sequence 2 Gap in sequence 1

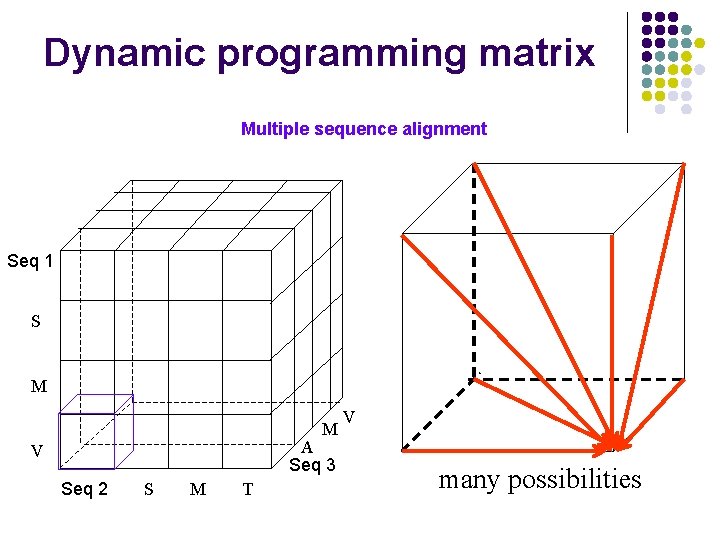
Dynamic programming matrix Multiple sequence alignment Seq 1 S M M A Seq 3 V Seq 2 S M T V many possibilities

DP Alignment Examples l All three match/mismatch l Sequence 1 & 2 match/mismatch with gap in 3 l Sequence 1 & 3 match/mismatch with gap in 2 l Sequence 2 & 3 match/mismatch with gap in 1 l Sequence 1 with gaps in 2 & 3 l Sequence 2 with gaps in 1 & 3 l Sequence 3 with gaps in 1 & 2 l Choose the largest value among the above seven possibilities

Computational Complexity l For protein sequences each 300 amino acid in length & excluding gaps, with DP algorithm Two sequences, 3002 comparisons l Three sequences, 3003 comparisons l N sequences, 300 N comparisons O(LN) L: length of the sequences; N: number of sequences l l The number of comparisons & memory required are too large for n > 3 and not practical

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

Star Alignments l l Heuristic method for multiple sequence alignments Select a sequence sc as the center of the star For each sequence s 1, …, sk such that index i c, perform a global alignment (using DP) Aggregate alignments with the principle “once a gap, always a gap. ”

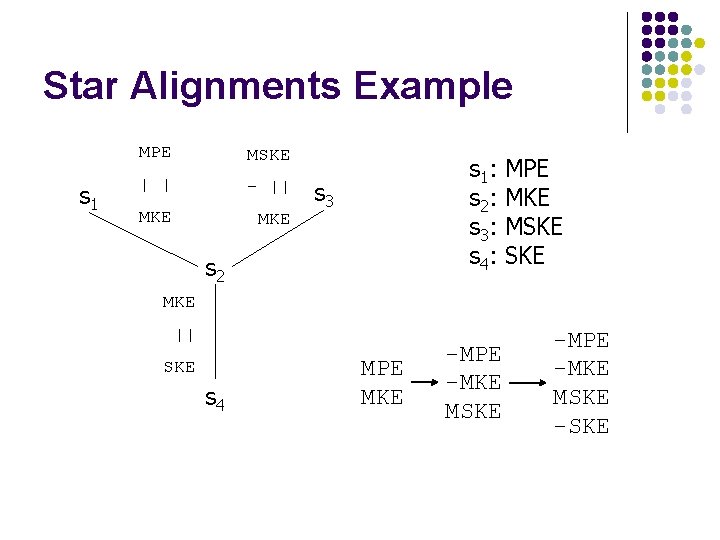
Star Alignments Example s 1 MPE MSKE | | - || MKE s 1 : s 2 : s 3 : s 4 : s 3 s 2 MPE MKE MSKE MKE || SKE s 4 MPE MKE -MPE -MKE MSKE -SKE

Choosing a center l l Try them all and pick the one with the best score Calculate all O(k 2) alignments, and pick the sequence sc that maximizes

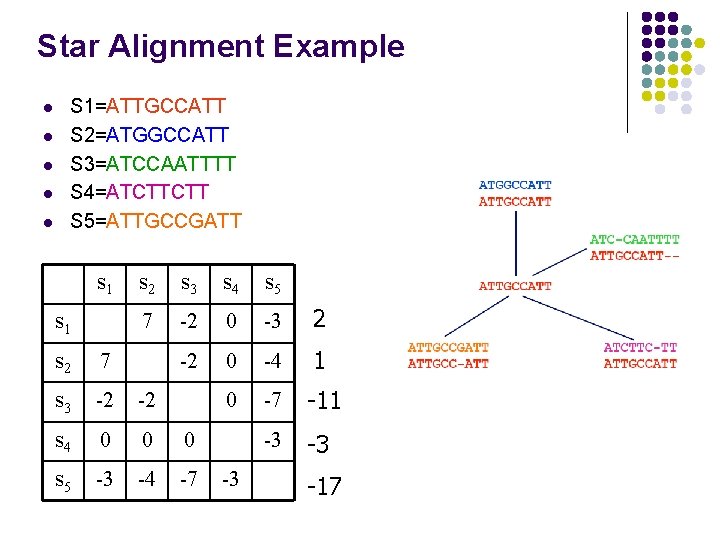
Star Alignment Example l l l S 1=ATTGCCATT S 2=ATGGCCATT S 3=ATCCAATTTT S 4=ATCTTCTT S 5=ATTGCCGATT s 1 s 2 s 3 s 4 s 5 7 -2 0 -3 2 -2 0 -4 1 0 -7 -11 -3 -3 s 2 7 s 3 -2 -2 s 4 0 0 0 s 5 -3 -4 -7 -3 -17

Star Alignments Example Merging Pairwise Alignment

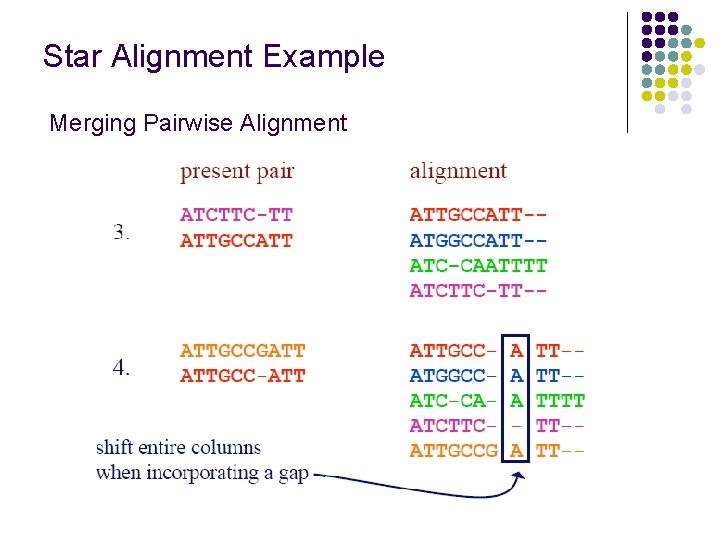
Star Alignment Example Merging Pairwise Alignment

Analysis l l l Assuming all sequences have length n O(n 2) to calculate global alignment O(k 2) global alignments to calculate Using a reasonable data structure for joining alignments, no worse than O(kl), where l is upper bound on alignment lengths O(k 2 n 2+kl)=O(k 2 n 2) overall cost

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

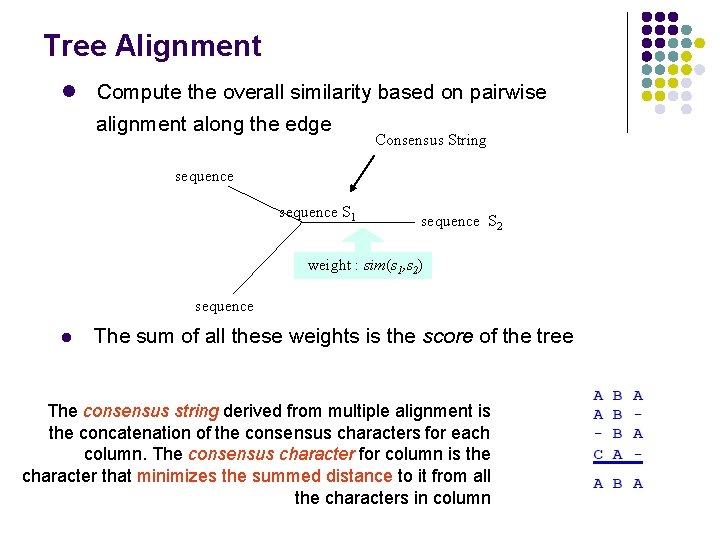
Tree Alignment l Compute the overall similarity based on pairwise alignment along the edge Consensus String sequence S 1 sequence S 2 weight : sim(s 1, s 2) sequence l The sum of all these weights is the score of the tree The consensus string derived from multiple alignment is the concatenation of the consensus characters for each column. The consensus character for column is the character that minimizes the summed distance to it from all the characters in column

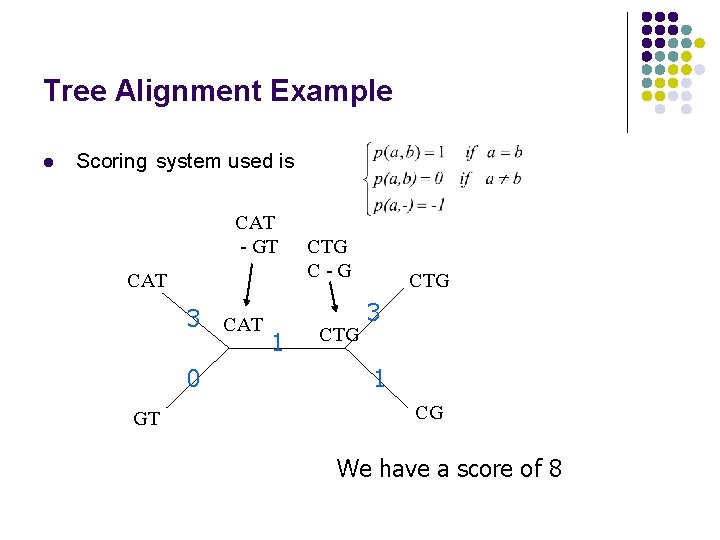
Tree Alignment Example l Scoring system used is CAT - GT CAT 3 CAT 0 GT 1 CTG C-G CTG 3 1 CG We have a score of 8

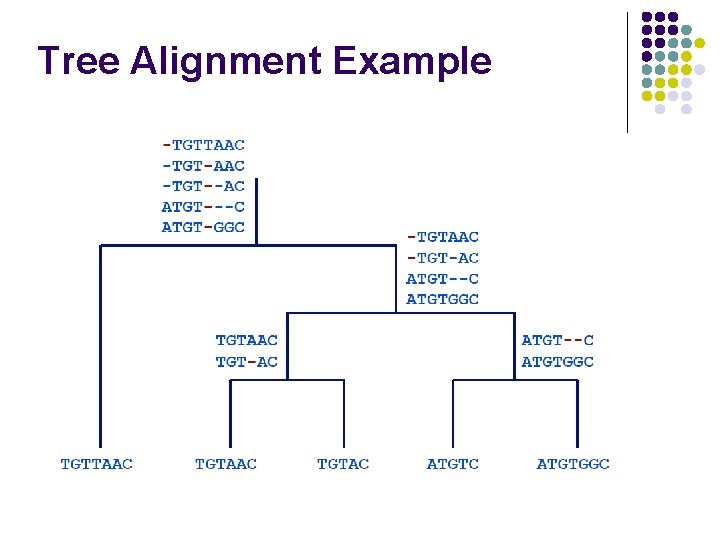
Tree Alignment Example

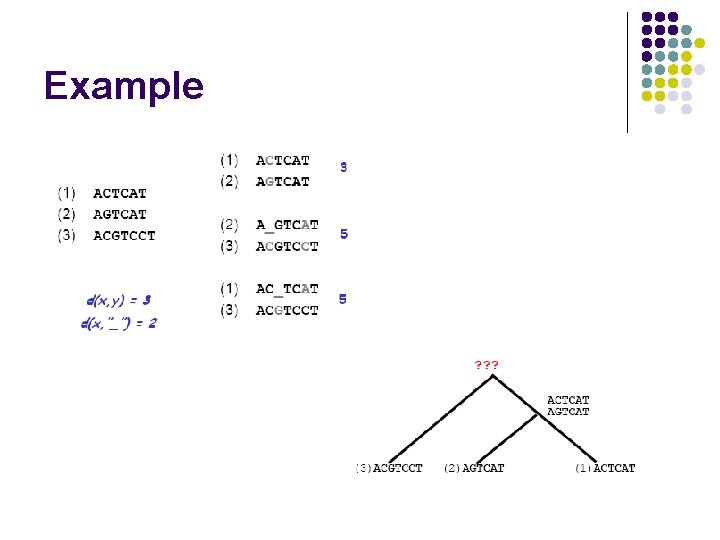
Example

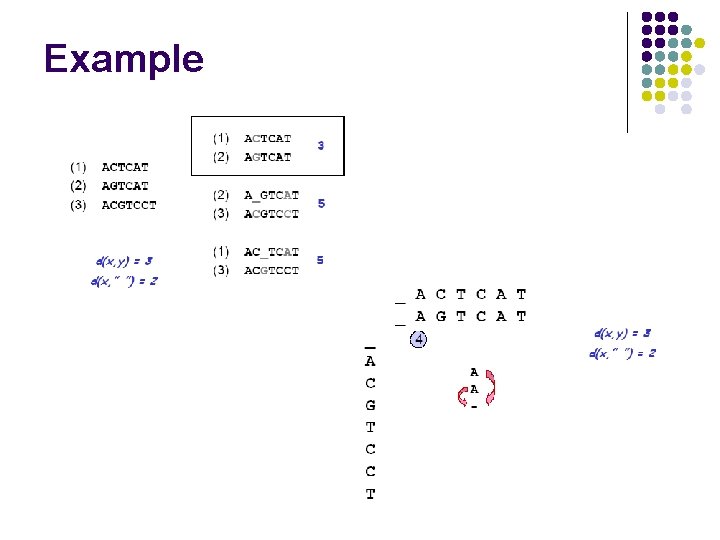
Example

Example

Example

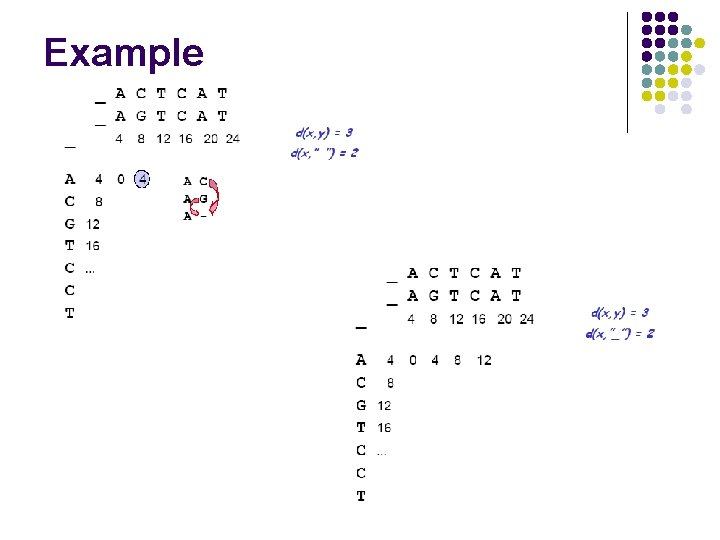
Example

Example

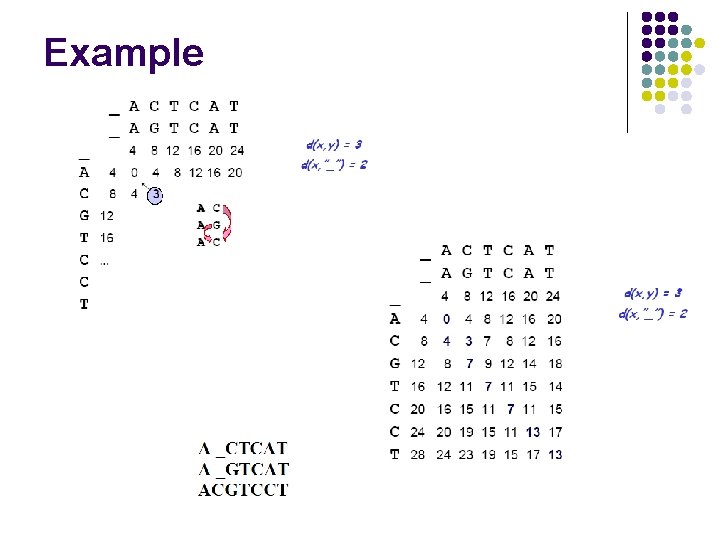
Example

Analysis l l We don’t know the correct tree Without the tree, the tree alignment problem is NP-complete l Likely only exponential time solution available (for optimal answers)

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

Progressive Methods l l l DP-based MSA program is limited in 3 sequences or to a small # of relatively short sequences Progressive alignments uses DP to build a msa starting with the most related sequences and then progressively adding less-related sequences or groups of sequences to the initial alignment Most commonly used approach

Progressive Methods Progressive alignment is heuristic. l It does not separate the process of scoring an alignment from the optimization algorithm l It does not directly optimize any global scoring function of “alignment correctness”. l It is fast, efficient and the results are reasonable. We will illustrate this using Clustal. W. l

Progressive MSA occurs in 3 stages 1. Do a set of global pairwise alignments (Needleman and Wunsch) 2. Create a guide tree 3. Progressively align the sequences

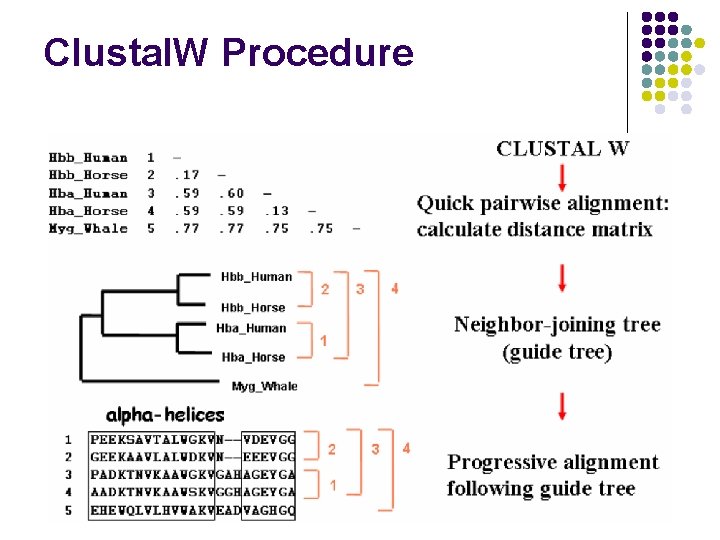
Clustal. W Procedure

Progressive Methods: Clustal. W l http: //www. ebi. ac. uk/clustalw/ l Clustal. W is a general purpose multiple alignment program for DNA or proteins. l Clustal. W: The W standing for “weighting” to represent the ability of the program to provide weights to the sequence and program parameters. l CLUSTALX provides a graphic interface

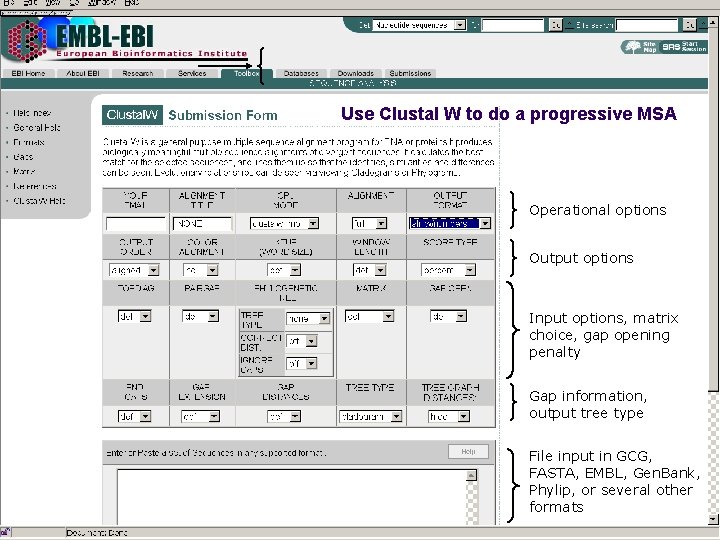
Use Clustal W to do a progressive MSA Operational options Output options Input options, matrix choice, gap opening penalty Gap information, output tree type File input in GCG, FASTA, EMBL, Gen. Bank, Phylip, or several other formats

Progressive MSA stage 3 of 3 : progressive alignment l l Make a MSA based on the order in the guide tree Start with the two most closely related sequences Then add the next closest sequence Continue until all sequences are added to the MSA

Problems w/ Progressive Alignment l Highly sensitive to the choice of initial pair to align. l l l The very first sequences to be aligned are the most closely related on the sequence tree. If alignment good, few errors in the initial alignment The more distantly related these sequences, the more errors Errors in alignment propagated to the MSA

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm

Iterative Methods l l l Results do NOT depend on the initial pairwise alignment (recall progressive methods) Starting with an initial alignment and repeatedly realigning groups of the sequences Repeat until one MSA doesn’t change significantly from the next. After iterations, alignments are better and better. An example is genetic algorithm approach.

Genetic Algorithms l l l A general problem solving method modeled on evolutionary change. Inspired by the biological evolution process Uses concepts of “Natural Selection” and “Genetic Inheritance” (Darwin 1859) Create a set of candidate solutions to your problem, and cause these solutions to evolve and become more and more fit over repeated generations. Use survival of the fittest, mutation, and crossover to guide evolution.

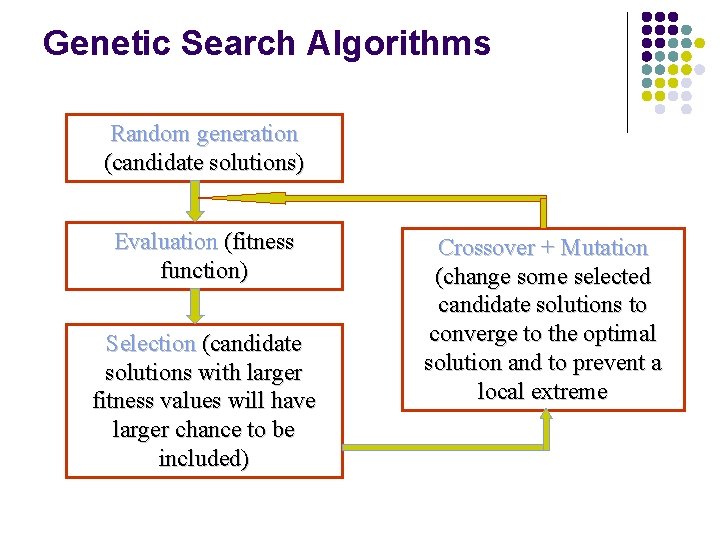
Genetic Search Algorithms Random generation (candidate solutions) Evaluation (fitness function) Selection (candidate solutions with larger fitness values will have larger chance to be included) Crossover + Mutation (change some selected candidate solutions to converge to the optimal solution and to prevent a local extreme

Outline l Multiple Sequence Alignment l l What, Why, and How Multiple Sequence Alignment Methods l l l Multidimensional dynamic programming Star Alignment Tree Alignment § l Progressive Alignment § Clustalw: a widely used algorithm Iterative Alignment § Genetic Algorithm