Cosmic Microwave Background Acoustic Oscillations Angular Power Spectrum

Cosmic Microwave Background Acoustic Oscillations, Angular Power Spectrum, Imaging and Implications for Cosmology Carlo Baccigalupi, March 31, 2004

Outline… • • Present: angular power Future: Imaging CMB cleaning Primordial non-Gaussianity Reionization Lensing …

The Present CMB: Measuring Angular Power
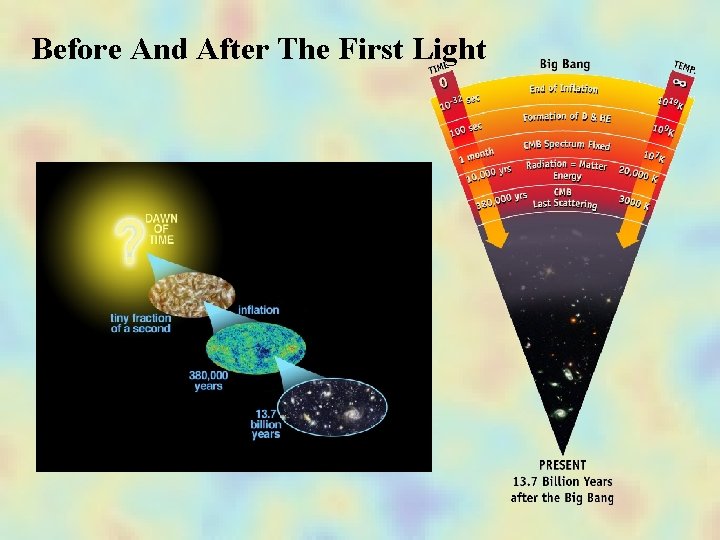
Before And After The First Light
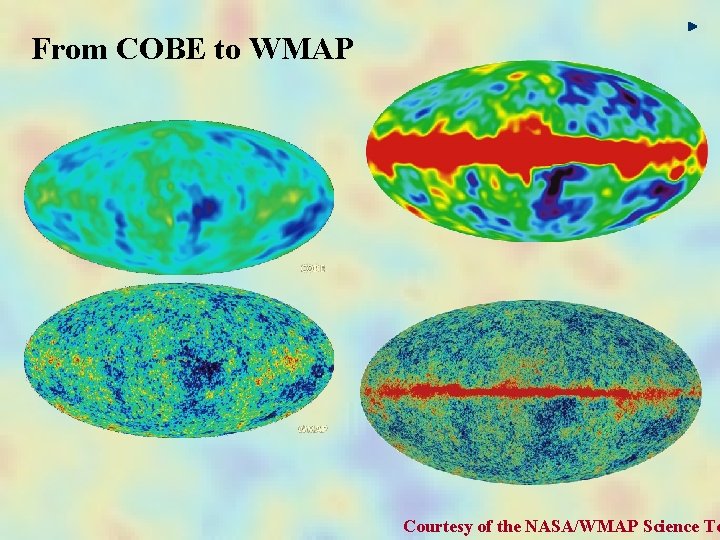
From COBE to WMAP Courtesy of the NASA/WMAP Science Te
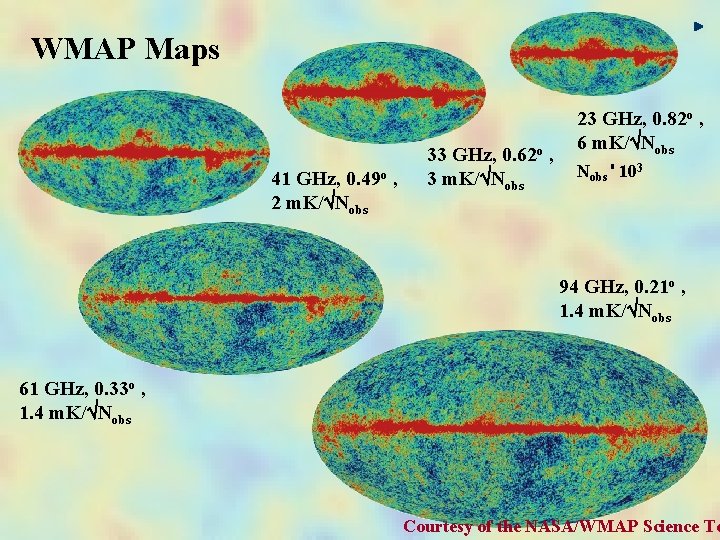
WMAP Maps 0. 49 o 41 GHz, 2 m. K/ Nobs , 33 GHz, 0. 62 o , 3 m. K/ Nobs 23 GHz, 0. 82 o , 6 m. K/ Nobs ' 103 94 GHz, 0. 21 o , 1. 4 m. K/ Nobs 61 GHz, 0. 33 o , 1. 4 m. K/ Nobs Courtesy of the NASA/WMAP Science Te
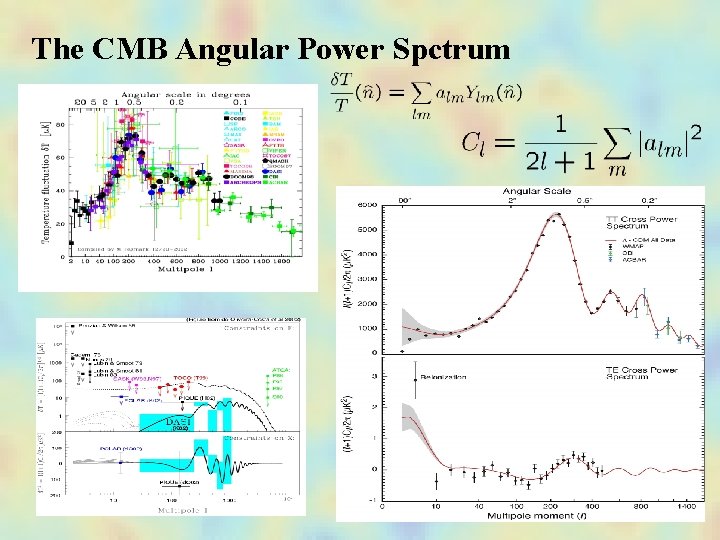
The CMB Angular Power Spctrum

Throwing Pebbles In The Primordial Pond + + Homogeneity & Isotropy Black Body Spectrum + Courtesy of the NASA/WMAP Science Te

The Sound Of The Early Universe Adiabati c Isocurvat ure



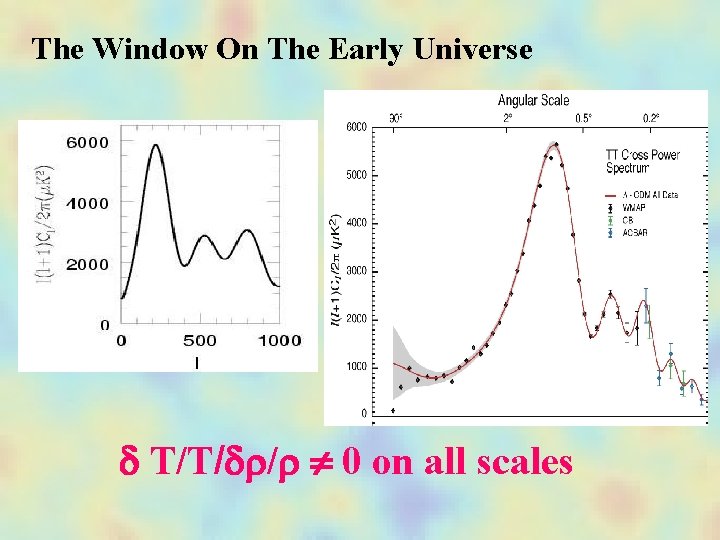
The Window On The Early Universe d T/T/dr/r 0 on all scales

Cosmological Parameters Basic Analysis: h, ns, k ¢ dns/dk, b h 2, m h 2, A, Extension: , m , w. DE, r WMAP, WMAP+ACBAR+CBI+2 d. F+Lyman b h 2 =0. 022§ 0. 001, 0. 0224 § 0. 0009 m h 2 =0. 14§ 0. 01, 0. 135 h=0. 71§ 0. 06, 0. 71 =0. 20§ 0. 07, 0. 17 § 0. 06 ns=0. 91§ 0. 06, 0. 93§ 0. 03 k ¢ dns/dk =. . . , -0. 031 A=0. 9 § 0. 1, 0. 83 +0. 008 -0. 009 +0. 04 -0. 03 +0. 016 +0. 09 0. 017 -0. 08

Extension: WMAP+ACBAR+CBI+HST+SNIa+(H 0>50 km/sec/Mpc): Extension: m =1. 02 § 0. 02 WMAP+ACBAR+CBI+2 d. F: h 2= imi/93. 5 e. V < 0. 0076 ´ m <0. 23 e. V Extension: w. DE WMAP+ACBAR+CBI+HST+SNIa+2 d. F: Extension: r w. DE < -0. 78 WMAP+ACBAR+CBI+2 d. F+infl. cons. rel. : r < -0. 71
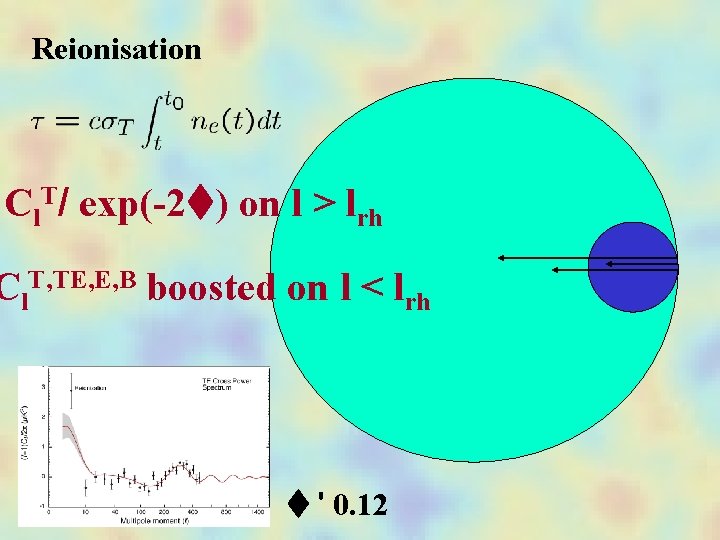
Reionisation Cl. T/ exp(-2 ) on l > lrh Cl. T, TE, E, B boosted on l < lrh ' 0. 12

The Future CMB: Imaging Cosmology
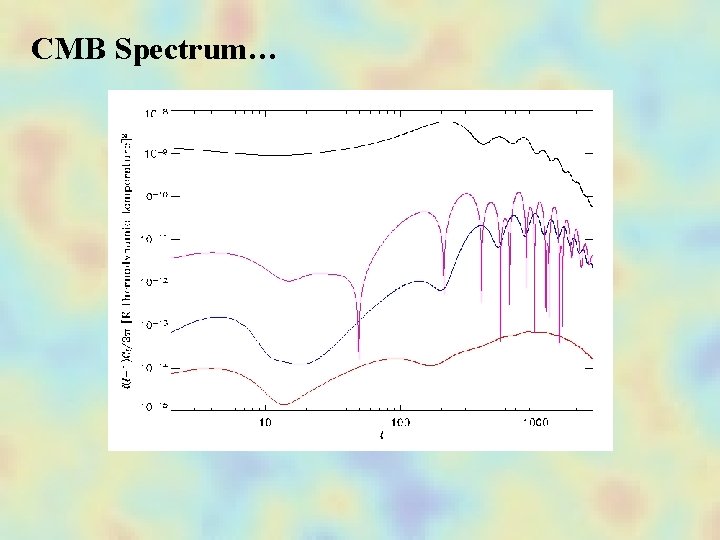
CMB Spectrum…
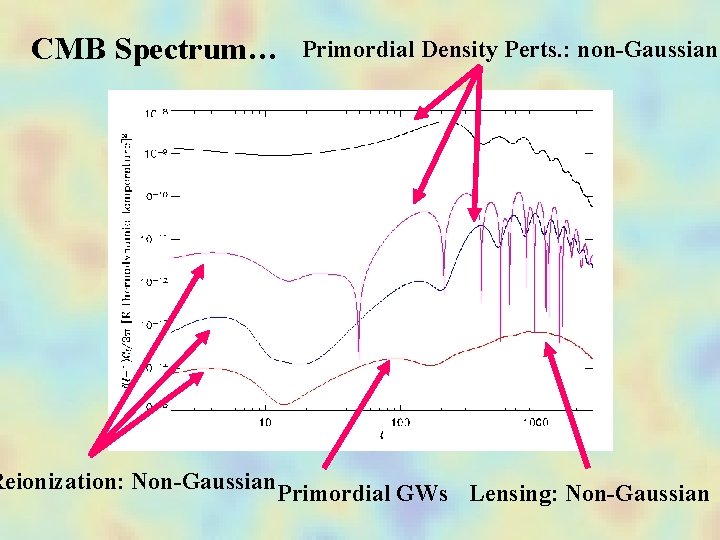
CMB Spectrum… Primordial Density Perts. : non-Gaussian? Reionization: Non-Gaussian Primordial GWs Lensing: Non-Gaussian
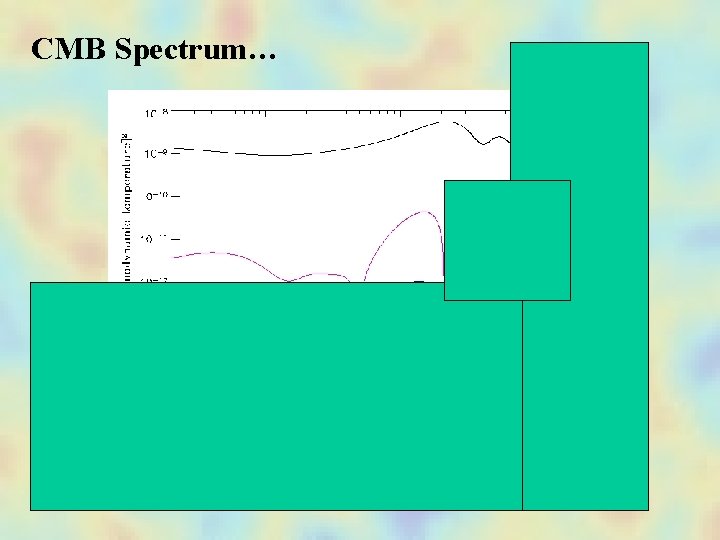
CMB Spectrum…
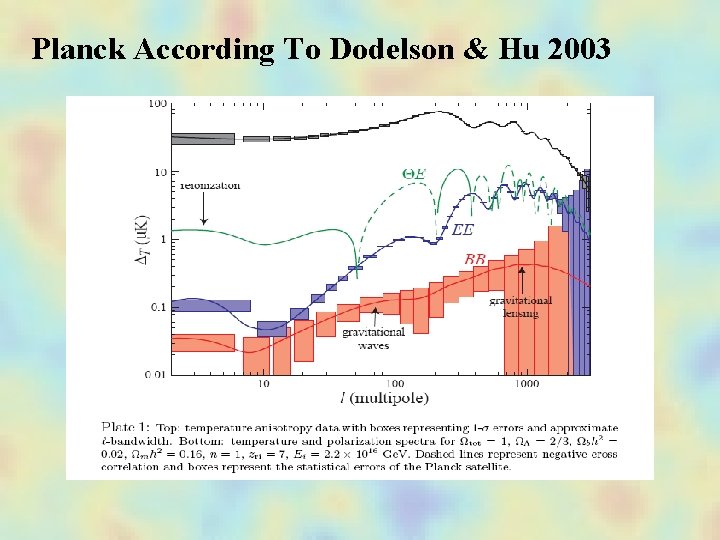
Planck According To Dodelson & Hu 2003
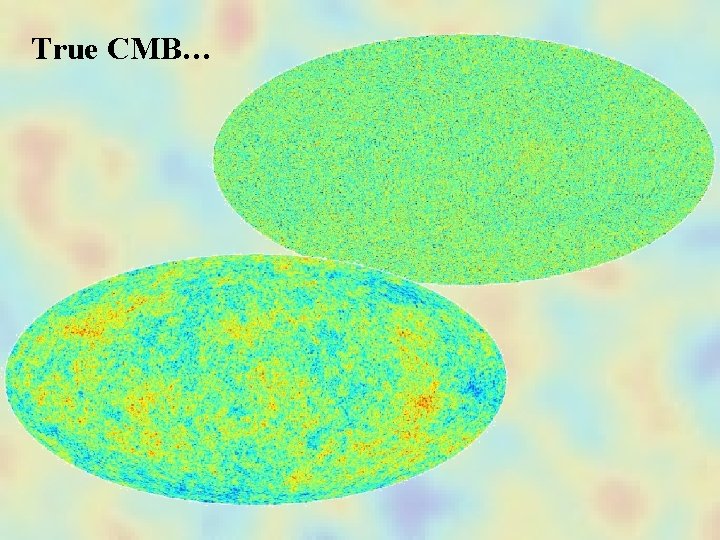
True CMB…

WMAP CMB…
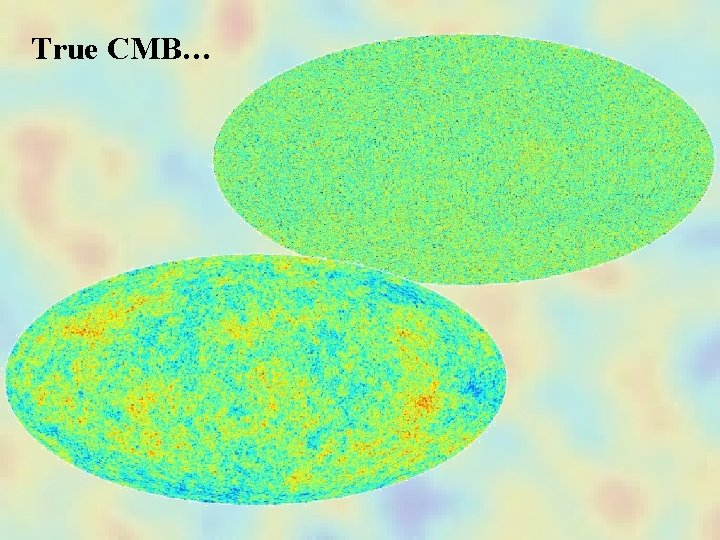
True CMB…
Planck CMB…
True CMB…
CMBpol CMB…
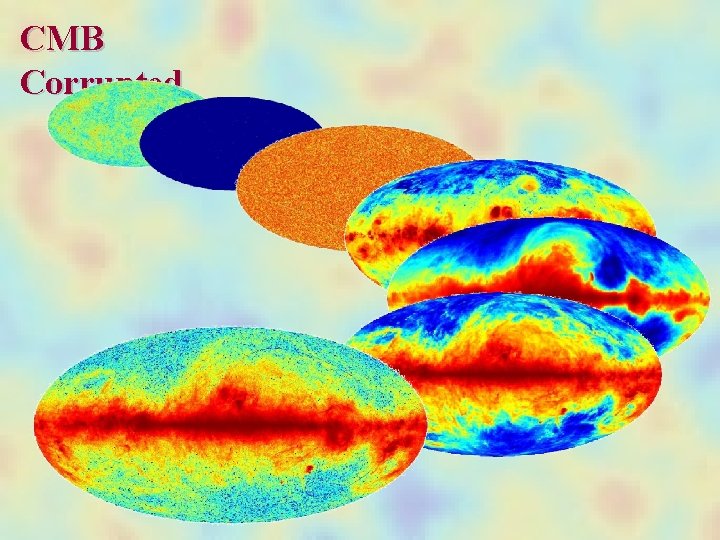
CMB Corrupted

The Future CMB: Foreground Removal
CMB Corrupted

Fast Independent Component Analysis (Fast. ICA) x=As+n, find W such that Wx=s+Wn Fast. ICA main loop: construct W row by row Choose initial w. Update wnew=E[xg(w. Tx)]through w. E(g’(w. Tx)) Compare with w. If not converged go back; if converged start up next row, keeping orthogonality
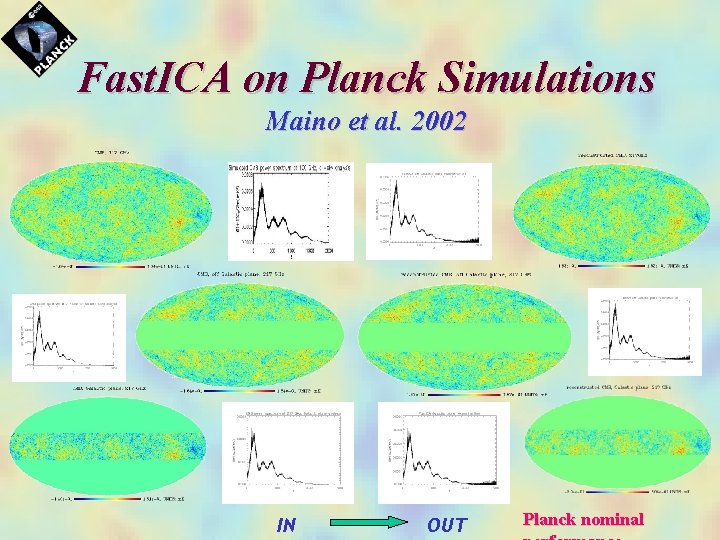
Fast. ICA on Planck Simulations Maino et al. 2002 IN OUT Planck nominal
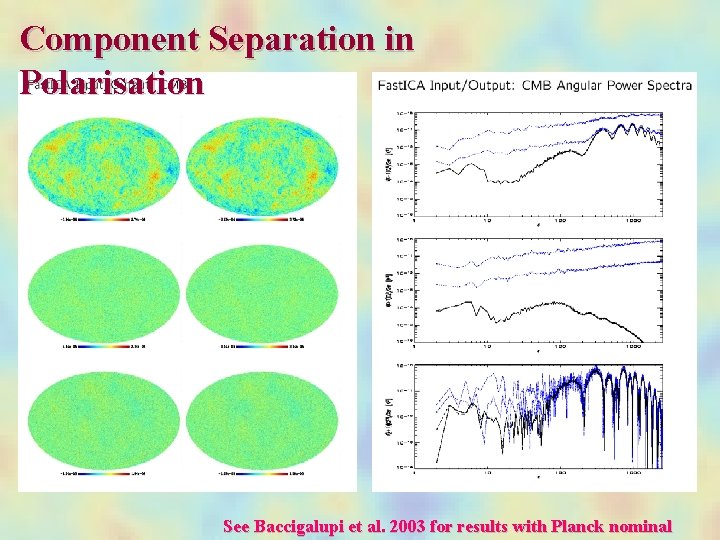
Component Separation in Polarisation See Baccigalupi et al. 2003 for results with Planck nominal

Fast. ICA and COBE • Perform Monte Carlo simulations to quantify the effect of noise distribution • Build Criteria to Identify Physical Components in a Heavy Noise Enviroment • Add priors to check quality and consistency of the results • Extract Cosmological Parameters and Foreground Science Maino et al. 2003
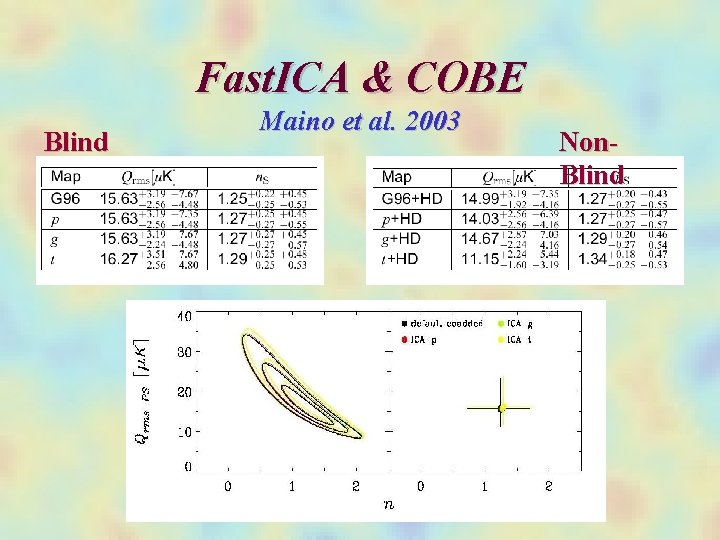
Fast. ICA & COBE Blind Maino et al. 2003 Non. Blind

The Future CMB: Imaging Physical Cosmology
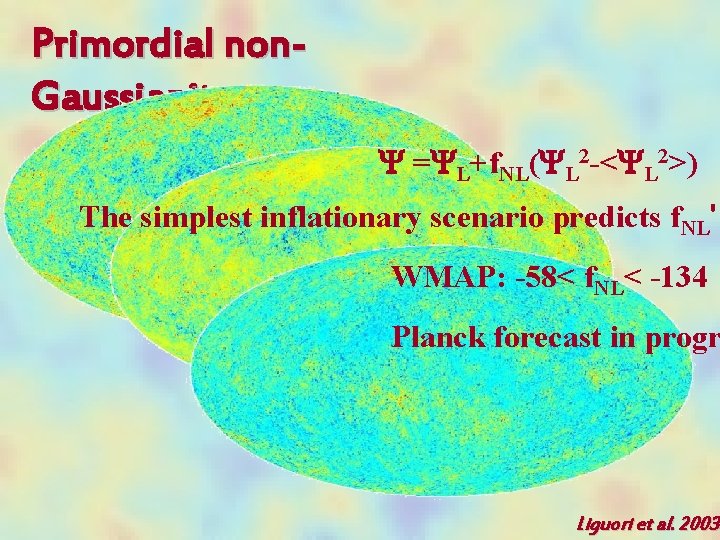
Primordial non. Gaussianity Y =YL+f. NL(YL 2 -<YL 2>) The simplest inflationary scenario predicts f. NL' WMAP: -58< f. NL< -134 Planck forecast in progr Liguori et al. 2003

Imaging Reionization… 9. 5 arcminutes Normal Stars in proto-galaxies 20% escape fraction d T/T CMB scattering on moving electorns t compatible with WMAP Salvaterra, Ferrara et al. 2004 in prep.
Dark Energy & CMB: beyond Cl s Giovi et al. 2003, PRD in press, astro-ph/0308118

CMB bispectrum Q (W ) ´ d. T(W )/T alm=s Q (W )Ylm(W )d. W Blm l`m`l``m``=alm al`m` al``m`` Bl l`l``=åm m` m`` (mlm`l`m``l``) alm al`m` al``m`` l l` l``
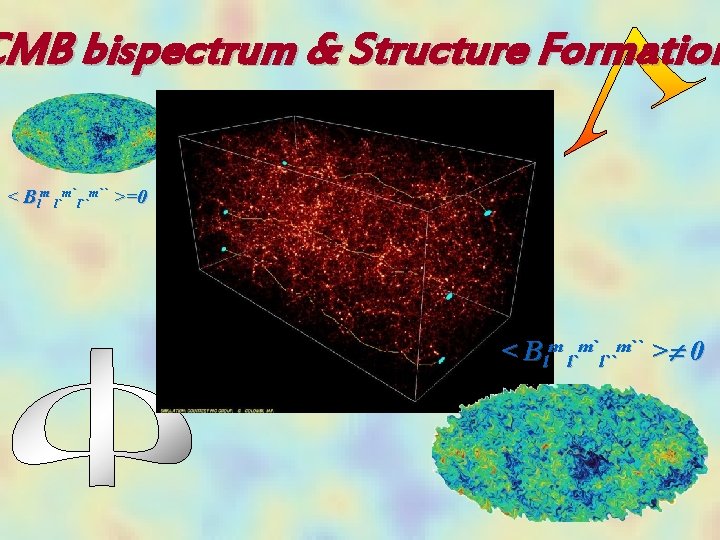
CMB bispectrum & Structure Formation < Blm l`m`l``m`` >=0 < Blm l`m`l``m`` > 0

CMB bispectrum & Structure Formation Q (W ) =Qlss(W +d. W)+QISW ' Qlss(W)+r. Qlss(W)¢d. W Q ISW(W )=2 s 0 decdr d. Y (r, W )/dh d. W =2 s 0 decdr[(r-rdec)/rdecr]Y(r, W) <Bl l`l``>=[(2 l+1)(2 l``+1)/16 p]1/2(0 l 0 l`0``l``) ¢ ¢ [l(l+1)- l`(l`+1)+ l``(l``+1) ] Cl Q(l``) +Perm. D(z)=[r(zdec)-r(z)]/r(zdec)r(z)3 Q(l)=s 0 dec D(z) F(z) dz F(z)=d. PY/dz|k=l/r(z) PY=(3 Wm 0 /2)2(H 0/ck)4 P(k, z)(1+z)2 P(k, z)=Akn. T(k, z)2 Hu & White 1997, Bartelmann & Schneider 2001, Komatsu & Spergel 2001, Verde & Spergel 2002
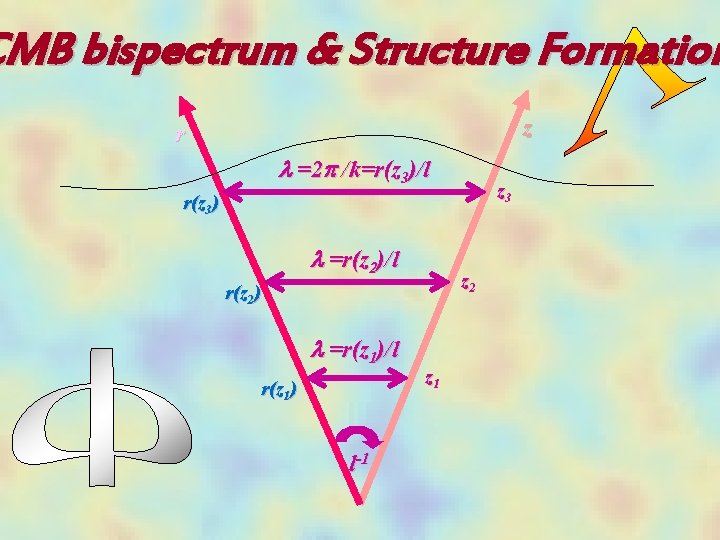
CMB bispectrum & Structure Formation z r l =2 p /k=r(z 3)/l z 3 r(z 3) l =r(z 2)/l z 2 r(z 2) l =r(z 1)/l r(z 1) l-1 z 1
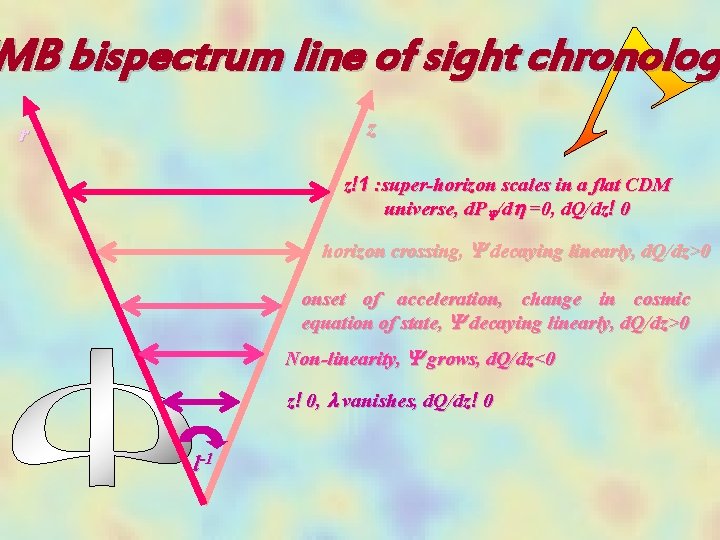
MB bispectrum line of sight chronolog z r z!1 : super-horizon scales in a flat CDM universe, d. PY/dh =0, d. Q/dz! 0 horizon crossing, Y decaying linearly, d. Q/dz>0 onset of acceleration, change in cosmic equation of state, Y decaying linearly, d. Q/dz>0 Non-linearity, Y grows, d. Q/dz<0 z! 0, l vanishes, d. Q/dz! 0 l-1
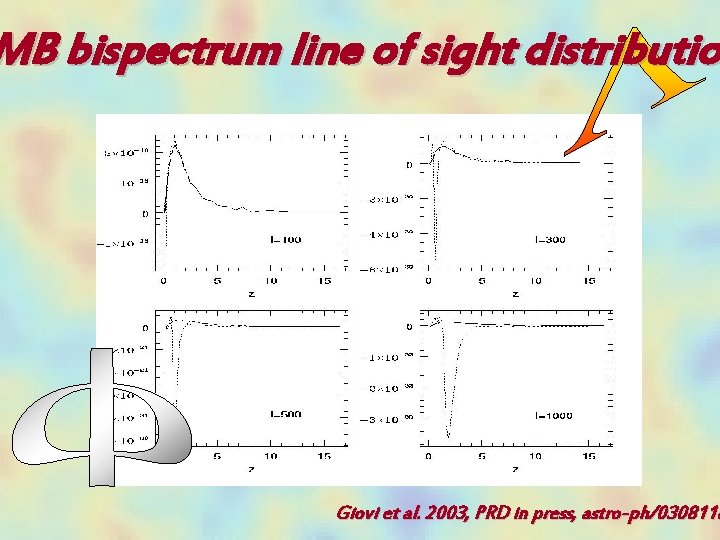
MB bispectrum line of sight distributio Giovi et al. 2003, PRD in press, astro-ph/0308118
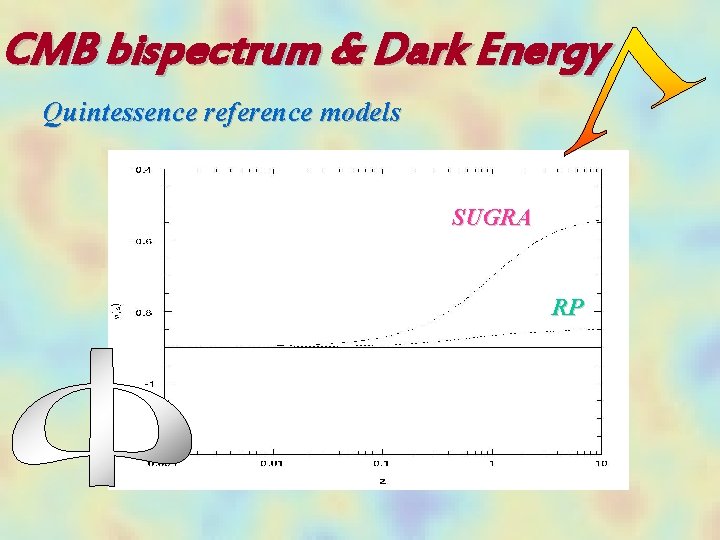
CMB bispectrum & Dark Energy Quintessence reference models SUGRA RP
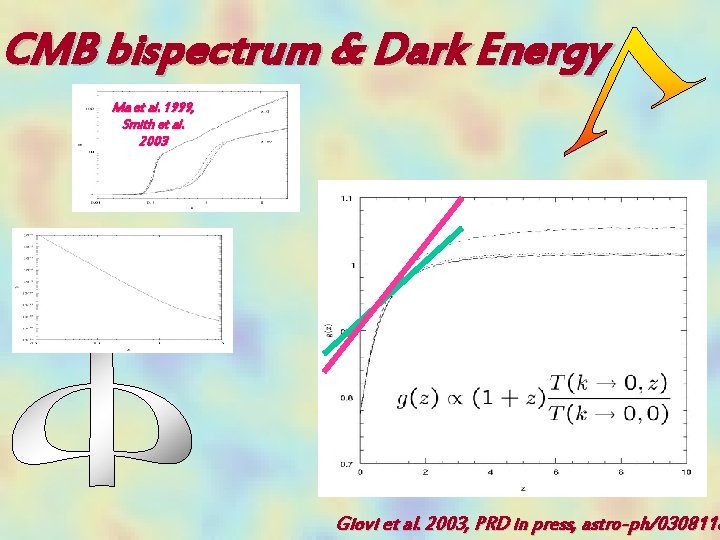
CMB bispectrum & Dark Energy Ma et al. 1999, Smith et al. 2003 Giovi et al. 2003, PRD in press, astro-ph/0308118
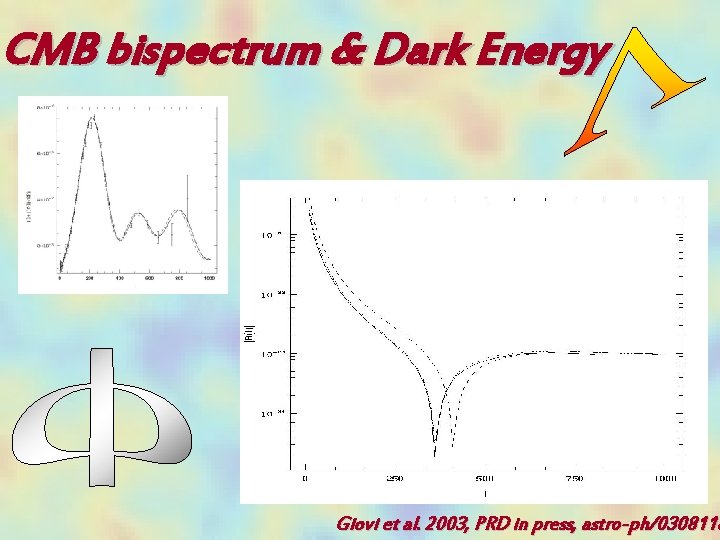
CMB bispectrum & Dark Energy Giovi et al. 2003, PRD in press, astro-ph/0308118
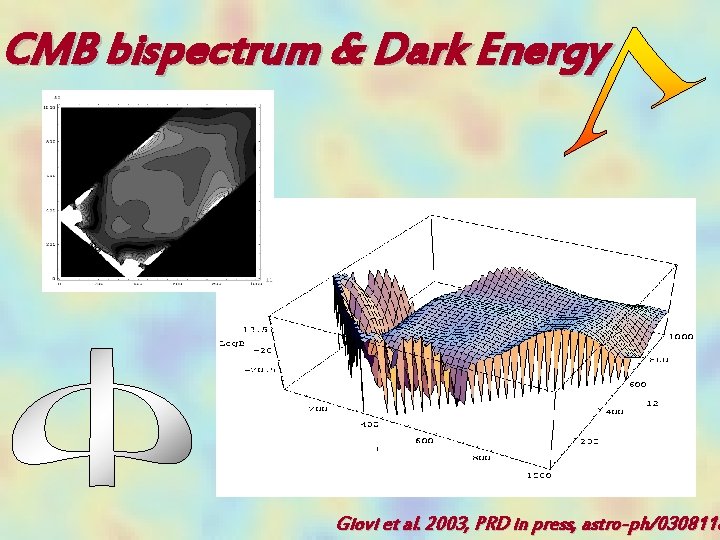
CMB bispectrum & Dark Energy Giovi et al. 2003, PRD in press, astro-ph/0308118
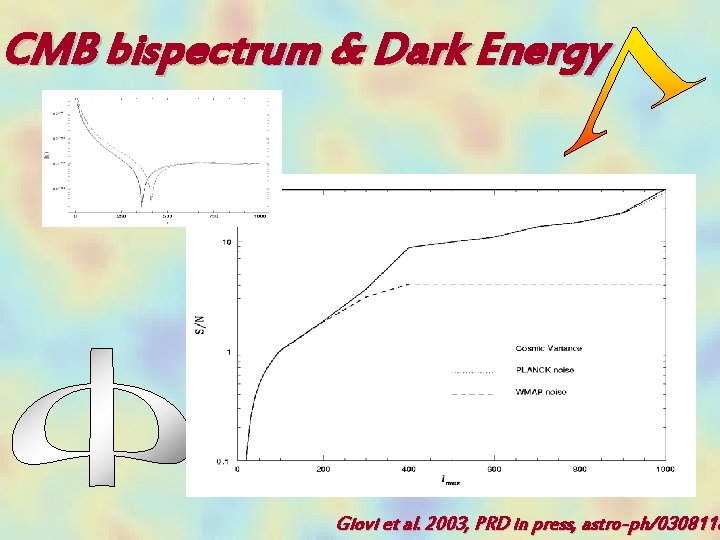
CMB bispectrum & Dark Energy Giovi et al. 2003, PRD in press, astro-ph/0308118

CMB bispectrum & Structure Formation < Blm l`m`l``m`` >=0 < Blm l`m`l``m`` > 0 d. W =2 s 0 decdr[(r-rdec)/rdecr]Y(r, W) Giovi, Liguori et al. 2004, in preparation

Continua… • Component Separation & WMAP… • Impact of CMB bispectrum on Planck Cosmological Parameter Estimation… • Weakly Lensed CMB Templates, Semianalytical… • Weakly Lensed CMB Templates, Numerical… • Weakly Lensed CMB Templates, Polarisation… • Weakly Lensed CMB Templates, Comparison with Gravitational Wave Signal…
- Slides: 52