Cosets Lagranges Theorem The most important single theorem

Cosets

Lagrange's Theorem • The most important single theorem in group theory. It helps answer: – How large is the symmetry group of a volleyball? A soccer ball? – How many groups of order 2 p where p is prime? (4, 6, 10, 14, 22, 26, …) – Is 2257 -1 prime? – Is computer security possible? – etc.

Cosets • Definition: Let H ≤ G and a in G. The left coset of H containing a is the set a. H = {ah | h in H} The right coset of H containing a is the set Ha = {ha | h in H} • In additive groups use a+H and H+a. • a is called the coset representative of a. H. • Similarly, a. Ha-1 ={aha-1 | h in H}

Cosets of K = {R 0, V} in D 4 • Some left cosets of K: DK = {DR 0, DV} = {D, R 90} R 180 K = {R 180 R 0, R 180 V} = {R 180, H} • Some right cosets of K: KD = {R 0 D, VD} = {D, R 270} KR 180 = {R 0 R 180, VR 180} = {R 180, H}

Cosets of K = {R 0, V} in D 4 • Left Cosets R 0 K = {R 0, V} = VK R 90 K = {R 90, D} = DK R 180 K = {R 180, H} = HK R 270 K = {R 270, D'}= D'K • Right Cosets KR 0 = {R 0, V} = KV KR 90 = {R 90, D'} = KD' KR 180 = {R 180, H} = KH KR 270 = {R 270, D} = KD

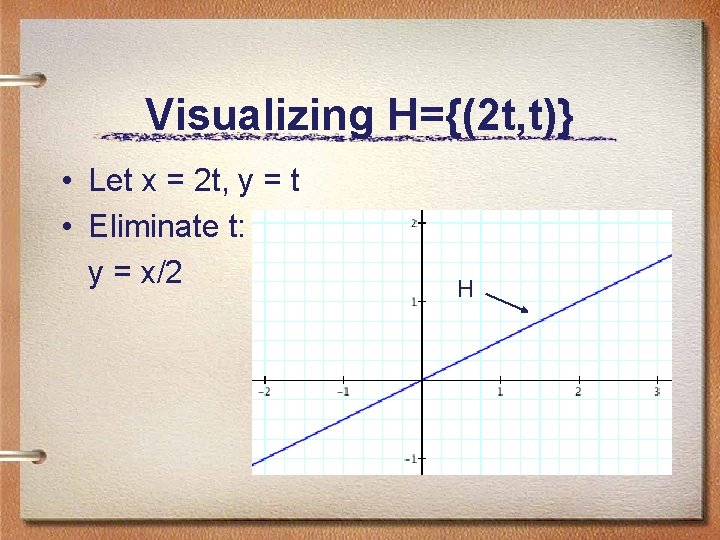
More cosets • Vectors under addition are a group: (a, b) + (c, d) = (a+c, b+d) Identity is (0, 0) Inverse of (a, b) is (-a, -b) Associativity is easy to verify. • H = {(2 t, t) | t in R} is a subgroup. Proof: (2 a, a) - (2 b, b) = (2(a-b), a-b)

Visualizing H={(2 t, t)} • Let x = 2 t, y = t • Eliminate t: y = x/2 H

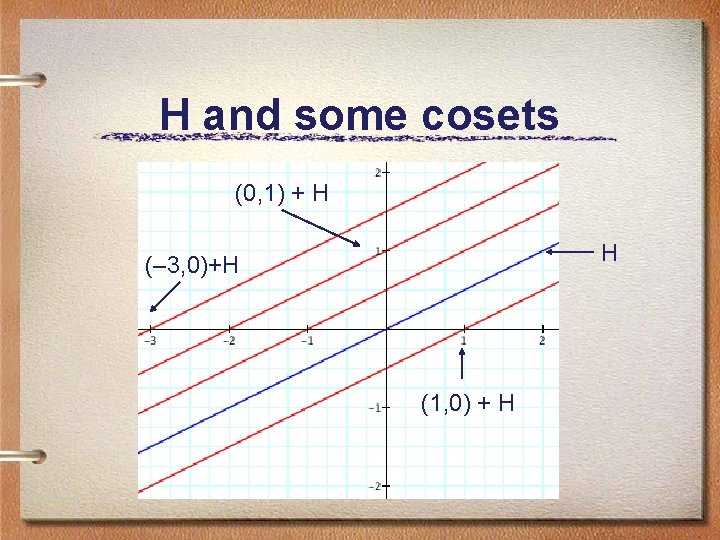
Cosets of H={(2 t, t) | t in R} • (a, b) + H = {(a+2 t, b+t)} Set x = a+2 t, y = b+t and eliminate t: y = b + (x-a)/2 The subgroup H is the line y = x/2. The cosets are lines parallel to y = x/2 !

H and some cosets (0, 1) + H H (– 3, 0)+H (1, 0) + H

Left Cosets of <(123)> in A 4 Let H = <(123)> { , (123), (132)} H = { , (123), (132)} (12)(34)H = {(12)(34), (243), (143)} (13)(24)H = {(13)(24), (142), (234)} (14)(23)H = {(14)(23), (134), (124)}

Properties of Cosets: • • • Let H be a subgroup of G, and a, b in G. 1. a belongs to a. H 2. a. H = H iff a belongs to H 3. a. H = b. H iff a belongs to b. H 4. a. H and b. H are either equal or disjoint 5. a. H = b. H iff a-1 b belongs to H 6. |a. H| = |b. H| 7. a. H = Ha iff H = a. Ha-1 8. a. H ≤ G iff a belongs to H

1. a belongs to a. H • Proof: a = ae belongs to a. H.

2. a. H=H iff a in H • Proof: (=>) Given a. H = H. By (1), a is in a. H = H. (<=) Given a belongs to H. Then (i) a. H is contained in H by closure. (ii) Choose any h in H. Note that a-1 is in H since a is. Let b = a-1 h. Note that b is in H. So h = (aa-1)h = a(a-1 h) = ab is in a. H It follows that H is contained in a. H By (i) and (ii), a. H = H

3. a. H = b. H iff a in b. H • Proof: (=>) Suppose a. H = b. H. Then a = ae in a. H = b. H. (<=) Suppose a is in b. H. Then a = bh for some h in H. so a. H = (bh)H = b(h. H) = b. H by (2).

4. a. H and b. H are either disjoint or equal. • Proof: Suppose a. H and b. H are not disjoint. Say x is in the intersection of a. H and b. H. Then a. H = x. H = b. H by (3). Consequently, a. H and b. H are either disjoint or equal, as required.

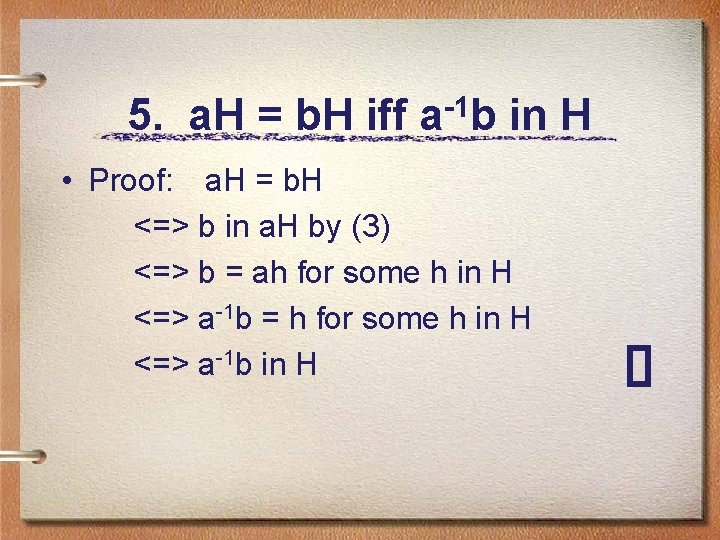
5. a. H = b. H iff a-1 b in H • Proof: a. H = b. H <=> b in a. H by (3) <=> b = ah for some h in H <=> a-1 b = h for some h in H <=> a-1 b in H

6. |a. H| = |b. H| • Proof: Let ø: a. H –>b. H be given by ø(ah) = bh for all h in H. We claim ø is one to one and onto. If ø(ah 1) = ø(ah 2), then bh 1 = bh 2 so h 1 = h 2. Therefore ah 1 = ah 2. Hence ø is one-to-one. ø is clearly onto. It follows that |a. H| = |b. H| as required.

a. H = Ha iff H = a. Ha-1 • Proof: a. H = Ha <=> each ah = h'a for some h' in H <=> aha-1 = h' for some h' in H <=> H = a. Ha-1.

a. H≤G iff a in H • Proof: (=>) Suppose a. H ≤ G. Then e in a. H. But e in e. H, so e. H and a. H are not disjoint. By (4), a. H = e. H = H. (<=) Suppose a in H. Then a. H = H ≤ G.