COSC 3340 Introduction to Theory of Computation University

COSC 3340: Introduction to Theory of Computation University of Houston Dr. Verma Lecture 4 1 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Formal definition of NFA acceptance l Define *(q, w) as a set of states: p ε *(q, w) if there is a directed path from q to p labeled w – l *(q 0, 1) = ? – l Ans: {q 0, q 1} *(q 0, 11) = ? – 2 Example: consider NFA of Lecture 3 Ans: {q 0, q 1, q 2} Lecture 4 Uof. H - COSC 3340 - Dr. Verma

NFA acceptance (contd. ) 3 l w is accepted by NFA M iff *(q 0, w) F is nonempty. l L(M) = {w in * | w is accepted by M}. Lecture 4 Uof. H - COSC 3340 - Dr. Verma

NFA vs. DFA l Is NFA more powerful than DFA? – l Theorem: – l For every NFA M there is an equivalent DFA M' Proof Idea: – – l Ans: No. NFA is in a set of states at any point during reading a string. DFA will use a lot of states to keep track of this. Important Assumption: – No transition labeled by epsilon. (Will get rid of this assumption later. ) 4 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Equivalent DFA construction. l l NFA M = (Q, , , s, F) DFA M' = (Q', , , s', F') where: – – Q' = 2 Q s' = {s} F' = {P | P F is nonempty} ({p 1, p 2, pm}, ) = *(p 1, ) *(p 2, ) . . . *(pm, ) i. e. find all the states that can be reached on from all the NFA states in a DFA state. 5 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

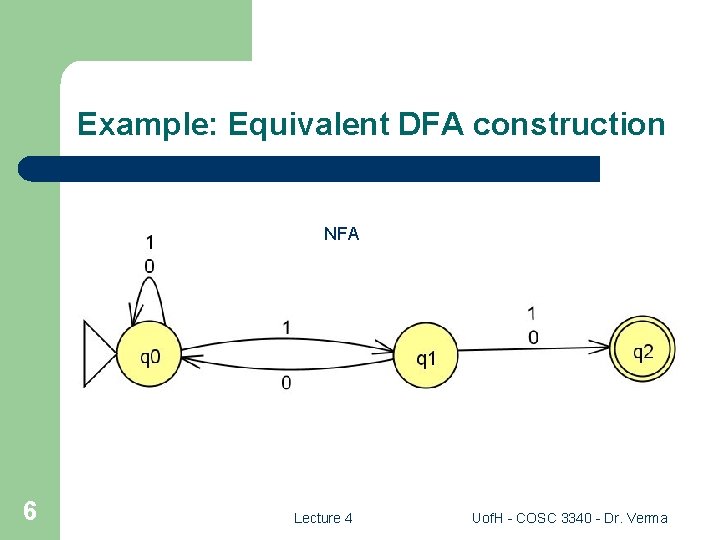
Example: Equivalent DFA construction NFA 6 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Equivalent DFA construction (contd. ) 7 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

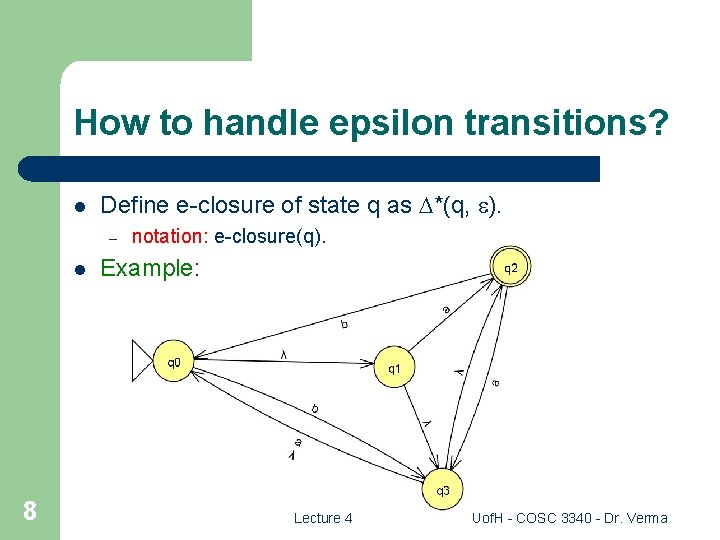
How to handle epsilon transitions? l Define e-closure of state q as *(q, ). – l 8 notation: e-closure(q). Example: Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Handling epsilon transitions (contd. ) l Extend e-closure to sets of states by: – e-closure({s 1, . . . , sm}) = e-closure(s 1) . . . e-closure(sm) Now let s' = e-closure({s}). and, ({p 1, . . . , pm}, ) = e-closure( *(p 1, )) . . . e-closure( *(pm, )) to complete construction of DFA. 9 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Example: Handling epsilon transitions. 10 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

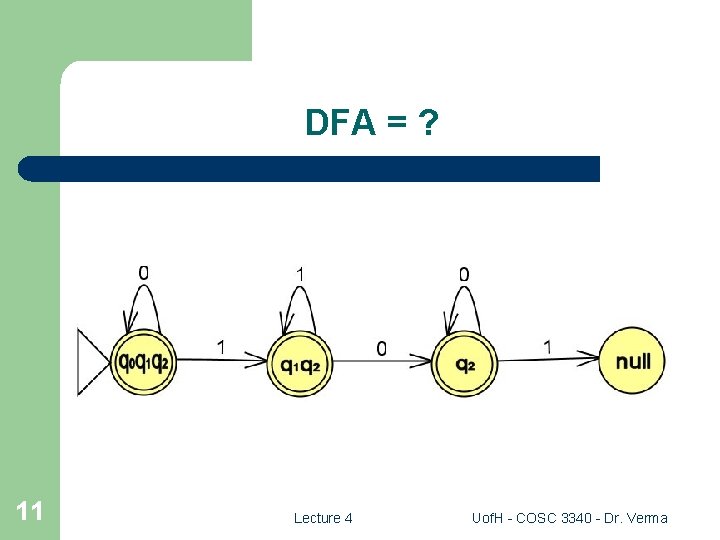
DFA = ? 11 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Language Operations 1. Concatenation. Notation: L L' or just LL' – 2. Kleene Star. Notation: L* – L* = { w in * | w = w 1. . . wk for some k >= 0 and each wi in L}. l Examples: if L = {a(2 n+1) | n >= 0}. L' = {b(2 n) | n > = 0}. l LL' = ? – Ans: LL' = {a(2 n+1) b(2 m) | n, m > = 0} L* = ? – Ans: {an | n >= 0} U, . , * are called regular operations. l l 12 L L' = {uv | u in L, v in L'}. Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Closure properties of regular languages. l l Previously we saw closure under and . New: Regular languages are closed under – – – 13 Concatenation Kleene star Complement. Lecture 4 Uof. H - COSC 3340 - Dr. Verma

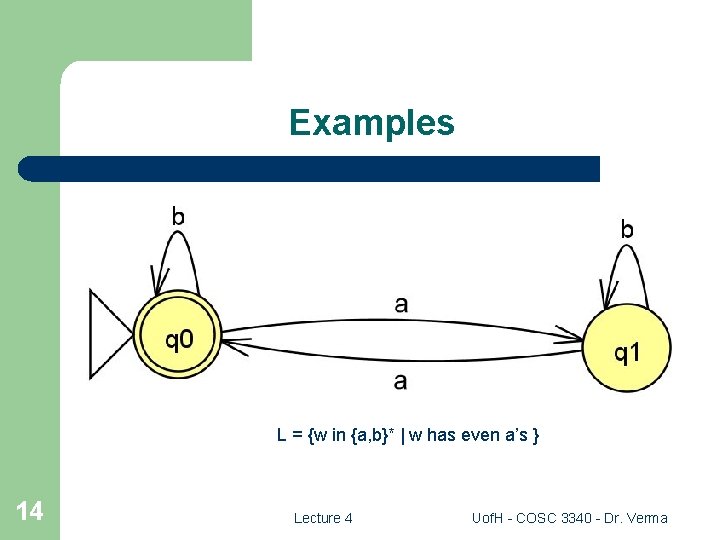
Examples L = {w in {a, b}* | w has even a’s } 14 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

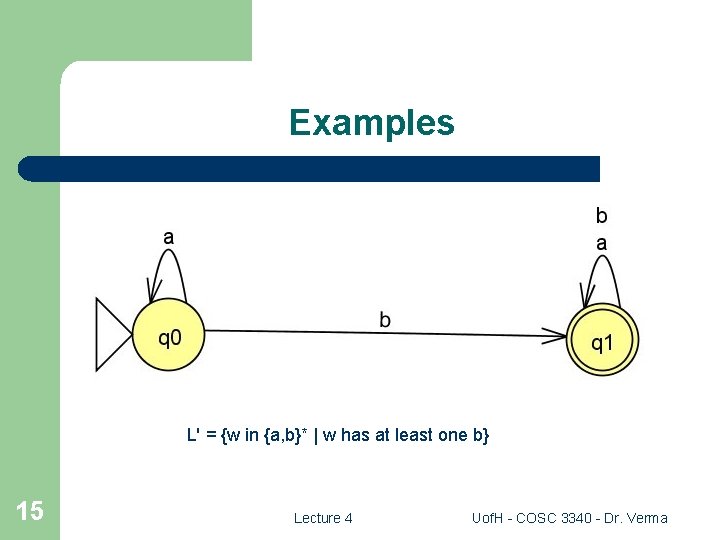
Examples L' = {w in {a, b}* | w has at least one b} 15 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

Construction for L L' 16 L’’ = (K, , , s, F) K = K 1 K 2 s = s 1 F = F 2 = 1 2 F 1 X {e} X {s 2} Lecture 4 Uof. H - COSC 3340 - Dr. Verma

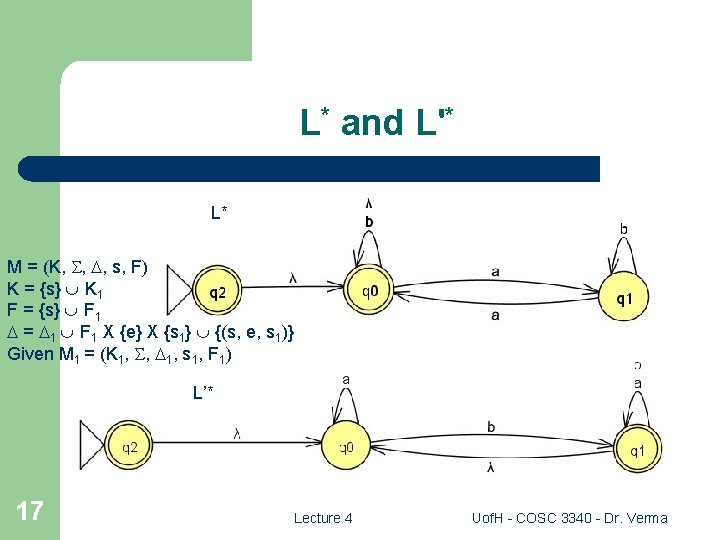
L* and L'* L* M = (K, , , s, F) K = {s} K 1 F = {s} F 1 = 1 F 1 X {e} X {s 1} {(s, e, s 1)} Given M 1 = (K 1, , 1, s 1, F 1) L’* 17 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

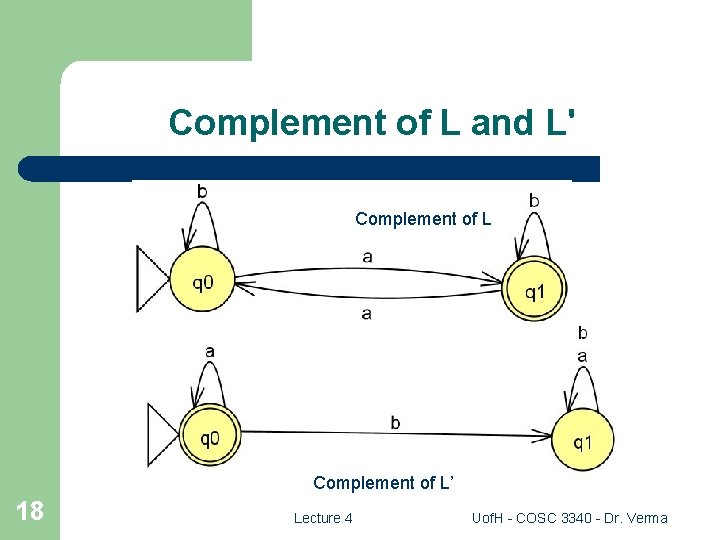
Complement of L and L' Complement of L’ 18 Lecture 4 Uof. H - COSC 3340 - Dr. Verma

General Construction for Complement DFA M = (K, , δ, s, F) K = K 1 s = s 1 F = K - F 1 δ = δ 1 L(M) = Complement of L(M 1) DFA M 1 = (K 1, , δ 1, s 1, F 1) Exercise: Will this construction work for NFAs? Explain your answer. 19 Lecture 4 Uof. H - COSC 3340 - Dr. Verma