COSC 2 P 05 Programming languages Lazy Evaluation

COSC 2 P 05 – Programming languages Lazy Evaluation Lazy evaluation: • an expression is evaluated if and only if its value is needed to compute the overall result Consequences: • elements are generated on demand so that complex intermediate structures are not necessarily expensive, e. g. , an intermediate list , • expression may describe infinite data structures, e. g, the infinite list of all prime numbers, • implications to program design. © M. Winter 11. 1

COSC 2 P 05 – Programming languages Example + h x y = x+x (9 -3) h (9 -3) (h 12 15) ® (9 -3) + (9 -3) ® 6+6 ® 12 (9 -3) + (9 -3) © M. Winter 11. 2

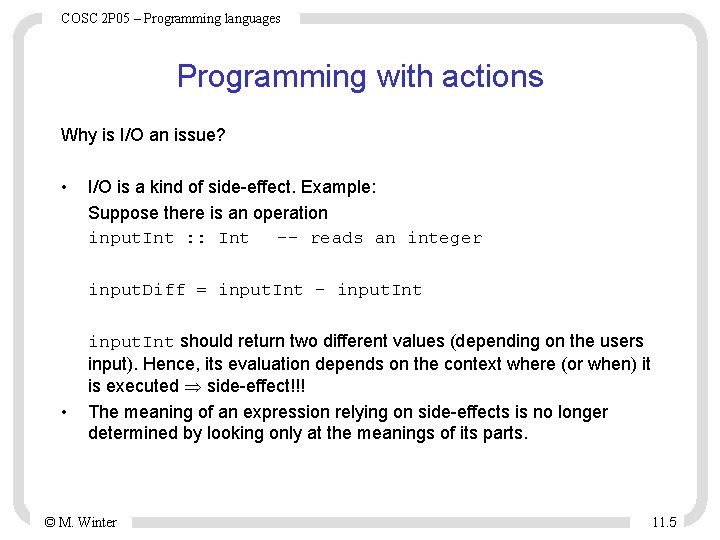
COSC 2 P 05 – Programming languages Infinite lists ones : : [Int] ones = 1 : ones [1, 1, 1, 1, ………………^C{Interrupted!}] add. First. Two : : [Int] -> Int add. First. Two (x: y: zs) = x+y add. First. Two ones ® add. First. Two (1: ones) ® add. First. Two (1: 1: ones) ® 1+1 ® 2 © M. Winter 11. 3

COSC 2 P 05 – Programming languages Example: prime numbers 2 3 4 5 6 7 2 3 5 7 8 9 9 10 11 12 13 11 13 The sieve of Eratosthenes primes : : [Integer] primes = sieve [2. . ] sieve : : [Integer] -> [Integer] sieve (x: xs) = x: sieve [ y | y <- xs, y `mod` x > 0] © M. Winter 11. 4

COSC 2 P 05 – Programming languages Programming with actions Why is I/O an issue? • I/O is a kind of side-effect. Example: Suppose there is an operation input. Int : : Int -- reads an integer input. Diff = input. Int – input. Int • input. Int should return two different values (depending on the users input). Hence, its evaluation depends on the context where (or when) it is executed side-effect!!! The meaning of an expression relying on side-effects is no longer determined by looking only at the meanings of its parts. © M. Winter 11. 5

COSC 2 P 05 – Programming languages Monadic I/O • • The Haskell type IO a is the type of I/O actions of type a, e. g. , the elements of a are somehow wrapped into an I/O container; the monad IO. An expression of type IO a is a program which will do some I/O and then return a value of type a. One way of looking at the IO a types is that they provide a simple imperative language for writing I/O programs on top of Haskell, without compromising the functional model of Haskell. This approach is called the monadic approach. It is more general and can be used to incorporate side-effect into a pure functional programming language (without its problems). © M. Winter 11. 6

COSC 2 P 05 – Programming languages Monads IO is a type constructor, i. e. , an operation on types. It maps a type a to the type IO a of I/O action on a. A characteristic of the I/O monad is that it allows to sequence operations. do line <- get. Line put. Str. Ln line What is the type of such a combinator which sequences the operations: (>>=) : : IO a -> (a -> IO b) -> IO b or, more general, for an arbitrary type constructor m, a combinator (>>=) : : m a -> (a -> m b) -> m b © M. Winter 11. 7

COSC 2 P 05 – Programming languages Monads (cont’d) class Monad m where (>>=) : : m a -> (a -> m b) -> m b return : : a -> m a (>>) : : m a -> m b fail : : String -> m a m >> k = m >>= _ -> k fail s = error s Requirements (informally): • The operation return x should simply return the value x, without any additional computational effect. • The sequencing given by >>= should be irrelevant of the way that expressions are bracketed. • >> acts like >>=, except that the value returned by the first expression is discarded rather than being passed to the second argument. • The value fail s corresponds to a computation that fails, giving the error message s. © M. Winter 11. 8

COSC 2 P 05 – Programming languages Logic Programming Languages Programming that uses a form of symbolic logic as a programming language is often called logic programming. The only widely used logic programming language is the language Prolog. Symbolic logic can be used for the three basic needs of formal logic: • to express propositions, • to express the relationships between propositions, and • to describe how new propositions can be inferred from other propositions that are assumed to be true. The particular form of symbolic logic that is used for logic programming is called first-order predicate calculus. © M. Winter 11. 9

COSC 2 P 05 – Programming languages Propositions • Atomic propositions (consist of compound terms) – Expresses a mathematical relationship – Composed of two parts • Functor, which is the function symbol that names the relation, • An ordered list of parameters, which together represent an element of the relation Examples: man(jake) like(bob, steak) man(fred) © M. Winter 11. 10

COSC 2 P 05 – Programming languages Compound Propositions © M. Winter 11. 11

COSC 2 P 05 – Programming languages Examples © M. Winter 11. 12

COSC 2 P 05 – Programming languages Clausal Form To simplify matters, a standard form for propositions is desirable. Clausal form, which is a relatively simple form of propositions, is one such standard form. All propositions can be expressed in clausal form. A proposition in clausal form has the following general syntax: The right side of a clausal form proposition is called the antecedent. The left side is called the consequent because it is the consequence of the truth of the antecedent. © M. Winter 11. 13

COSC 2 P 05 – Programming languages Proving Theorems (Resolution) The process of inferring a proposition from two propositions using the rule outlined here is called resolution. © M. Winter 11. 14

COSC 2 P 05 – Programming languages Proving Theorems (Resolution) Resolution is actually more complex than these simple examples illustrate. In particular, the presence of variables in propositions requires resolution to find values for those variables that allow the matching process to succeed. This process of determining useful values for variables is called unification. The temporary assigning of values to variables to allow unification is called instantiation. © M. Winter 11. 15

COSC 2 P 05 – Programming languages Horn Clauses Theorem proving is the basis for logic programming. Resolution on a hypotheses and a goal that are general propositions, even if they are in clausal form, is often not practical. Although it may be possible to prove a theorem using clausal form propositions, it may not happen in a reasonable amount of time. One way to simplify the resolution process is to restrict the form of the propositions. Horn clauses only can be in one of two forms: • They have either a single atomic proposition on the left side (rule) • or an empty left side (fact). © M. Winter 11. 16

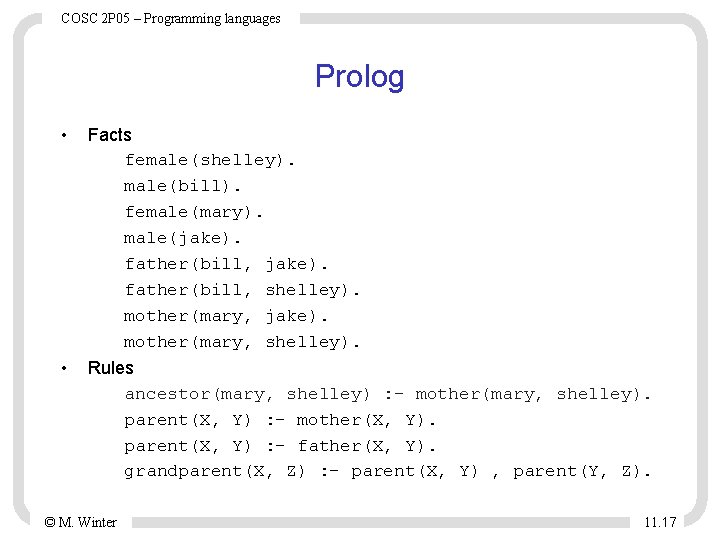
COSC 2 P 05 – Programming languages Prolog • Facts female(shelley). male(bill). female(mary). male(jake). father(bill, shelley). mother(mary, jake). mother(mary, shelley). • Rules ancestor(mary, shelley) : - mother(mary, shelley). parent(X, Y) : - mother(X, Y). parent(X, Y) : - father(X, Y). grandparent(X, Z) : - parent(X, Y) , parent(Y, Z). © M. Winter 11. 17

COSC 2 P 05 – Programming languages Prolog • • • Goal statement (or query) man(fred). father(X, mike). The system will respond with either yes or no. – The answer yes means that the system has proved the goal was true under the given database of facts and riles (the program). – The answer no means that either the goal was determined to be false or the system was simply unable to prove it. In addition, the system will attempt to find an instantiation of all variables that results in a true value for the goal. © M. Winter 11. 18