COSC 2 P 05 Programming languages Imperative languages

COSC 2 P 05 – Programming languages Imperative languages • • • Von Neumann model: – store with addressable locations machine code: – effect achieved by changing contents of store locations – instructions executed in sequence, flow of control altered by jumps imperative language: – variable corresponds to store location – instructions executed in sequence, flow of control altered by conditional and loop statements – efficient implementation since close to design of conventional computers © M. Winter 10. 1

COSC 2 P 05 – Programming languages Functional languages • • computational model: lambda calculus mathematical functions: domain, range functional languages achieve effect by applying functions functional vs. imperative languages – store location – assignment statement vs. application of a function (expressions) • side-effects • aliasing • referential transparency © M. Winter 10. 2

COSC 2 P 05 – Programming languages Features of functional languages • • usually strongly typed (modern languages) algebraic type definitions – mathematical based notation – no (implicit) pointers higher-order functions – can accept functions as parameters – can return functions as results recursion as a basic principle application of rewrite rule: – function call replaced by code body run-time overhead garbage collection slogan: define “what to do”, not “how to do” © M. Winter 10. 3

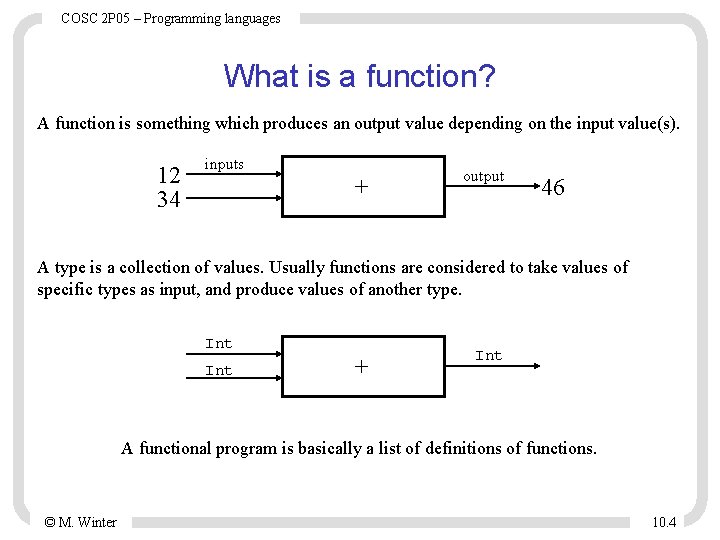
COSC 2 P 05 – Programming languages What is a function? A function is something which produces an output value depending on the input value(s). 12 34 inputs + output 46 A type is a collection of values. Usually functions are considered to take values of specific types as input, and produce values of another type. Int + Int A functional program is basically a list of definitions of functions. © M. Winter 10. 4

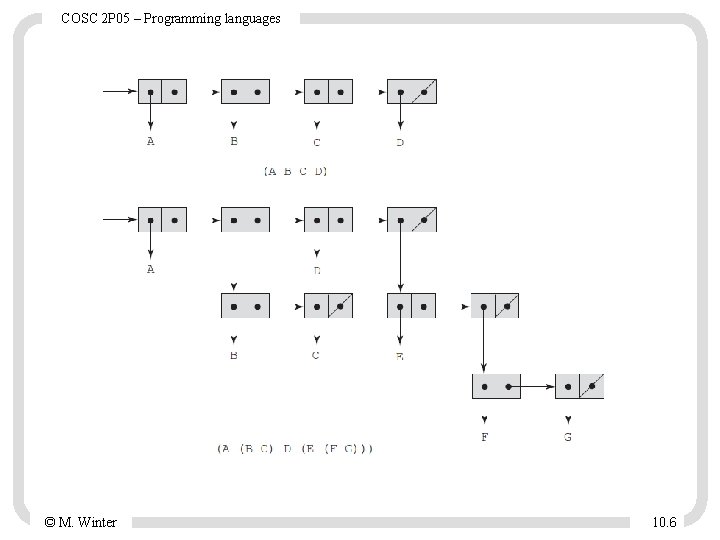
COSC 2 P 05 – Programming languages LISP The oldest and most widely used is Lisp (or one of its descendants), which was developed by John Mc. Carthy at MIT in 1959. • all Lisp dialects include imperative-language features, such as imperative-style variables, assignment statements, and iteration. Data types • There were only two categories of data objects in the original Lisp: atoms and lists. (A B C D) (A (B C) D (E (F G))) © M. Winter 10. 5

COSC 2 P 05 – Programming languages © M. Winter 10. 6

COSC 2 P 05 – Programming languages LISP Mc. Carthy believed that list processing could be used to study computability. One of the common requirements of the study of computation is that one must be able to prove certain computability characteristics of the whole class of whatever model of computation is being used (universal Lisp function). • Functions need to be expressed in the same way as data. (+ 5 7) (LAMBDA (x) (* x x)) • • Universal LISP function EVAL as interpreter. Dynamic scope © M. Winter 10. 7

COSC 2 P 05 – Programming languages Scheme The Scheme language, which is a dialect of Lisp, was developed at MIT in the mid-1970 s. A Scheme interpreter in interactive mode is an infinite read-evaluate-print loop (often abbreviated as REPL; also used by Ruby and Python). Scheme uses static scope. (DEFINE (function_name parameters) (expression) ) (DEFINE pi 3. 14159) (DEFINE two_pi (* 2 pi)) (DEFINE (square number) (* number)) © M. Winter 10. 8

COSC 2 P 05 – Programming languages • Output functions (DISPLAY expression) (NEWLINE) • Control flow (DEFINE (factorial n) (IF (<= n 1) 1 (* n (factorial (− n 1))) )) (DEFINE (leap? year) (COND ((ZERO? (MODULO year 400)) #T) ((ZERO? (MODULO year 100)) #F) (ELSE (ZERO? (MODULO year 4))) )) © M. Winter 10. 9

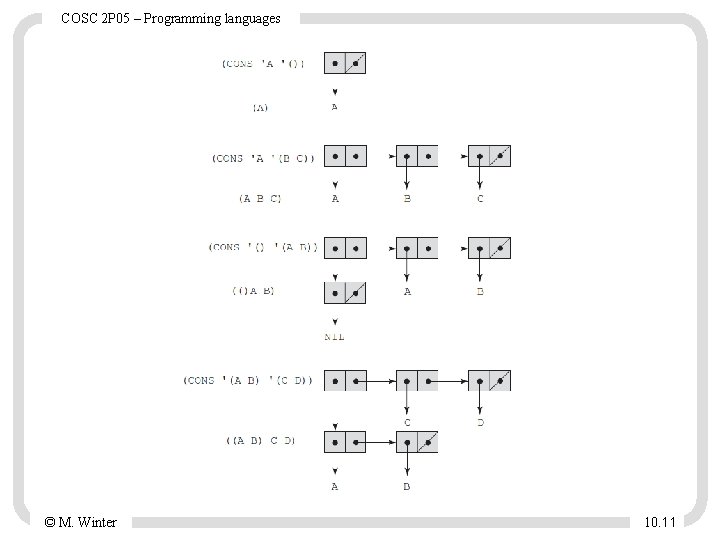
COSC 2 P 05 – Programming languages • List functions – QUOTE A or ‘A to avoid evaluation – CAR head function; CDR tail function (CAR '(A B C)) returns A (CAR '((A B) C D)) returns (A B) (CAR 'A) is an error because A is not a list (CAR '(A)) returns A (CAR '()) is an error (CDR '(A B C)) returns (B C) (CDR '((A B) C D)) returns (C D) (CDR 'A) is an error (CDR '(A)) returns () (CDR '()) is an error – CONS list construction © M. Winter 10. 10

COSC 2 P 05 – Programming languages © M. Winter 10. 11

COSC 2 P 05 – Programming languages (DEFINE (member atm a_list) (COND ((NULL? a_list) #F) ((EQ? atm (CAR a_list)) #T) (ELSE (member atm (CDR a_list))) )) (DEFINE (equal list 1 list 2) (COND ((NOT (LIST? list 1)) (EQ? list 1 list 2)) ((NOT (LIST? list 2)) #F) ((NULL? list 1) (NULL? list 2)) ((NULL? list 2) #F) ((equal (CAR list 1) (CAR list 2)) (equal (CDR list 1) (CDR list 2))) (ELSE #F) )) © M. Winter 10. 12

COSC 2 P 05 – Programming languages (DEFINE (map fun a_list) (COND ((NULL? a_list) '()) (ELSE (CONS (fun (CAR a_list)) (map fun (CDR a_list)))) )) (map (LAMBDA (num) (* num num)) '(3 4 2 6)) © M. Winter 10. 13

COSC 2 P 05 – Programming languages COMMON LISP Common Lisp (Steele, 1990) was created in an effort to combine the features of several early 1980 s dialects of Lisp, including Scheme, into a single language. • Dynamic and static scope • Large and complex language © M. Winter 10. 14

COSC 2 P 05 – Programming languages ML ML (Milner et al. , 1997) is a static-scoped functional programming language, like Scheme. • ML is a strongly typed language. • ML has type declarations for function parameters and the return types of functions, although because of its type inferencing they are often not used. The type of every variable and expression can be statically determined. • ML, like other functional programming languages, does not have variables in the sense of the imperative languages. It does have identifiers, which have the appearance of names of variables in imperative languages. However, these identifiers are best thought of as names for values. • Ocaml dialect with added object-orientation. • F# uses OCaml as core language. It is a first-class language in the. NET framework. © M. Winter 10. 15

COSC 2 P 05 – Programming languages fun square(x : int) : int = x * x; fun square(x : int) = x * x; fun square(x) = x * x; fun fact(n : int) : int = if n <= 1 then 1 else n * fact(n − 1); • Pattern matching fun fact(0) = 1 | fact(1) = 1 | fact(n : int): int = n * fact(n − 1); fun length([]) = 0 | length(h : : t) = 1 + length(t); © M. Winter 10. 16

COSC 2 P 05 – Programming languages Haskell (Thompson, 1999) is similar to ML in that it uses a similar syntax, is static scoped, is strongly typed, and uses the same type inferencing method. • Overloading of functions via classes • List comprehension • Lazy evaluation (non-strict semantics) • Fully functional, no imperative features; IO using monads fact © M. Winter : : int -> int 0 = 1 1 = 1 n = n * fact (n - 1) 10. 17

COSC 2 P 05 – Programming languages Overloading The definition elem : : a -> [a] -> Bool elem x [] = False elem x (y: ys) = (x == y) || elem x ys will cause an error because this definition requires that (==) : : a -> Bool for an arbitrary type a is already defined. elem. Bool : : Bool -> [Bool] -> Bool elem. Bool x [] = False elem. Bool x (y: ys) = (x ==Bool y) || elem. Bool x ys elem. Int : : Int -> [Int] -> Bool elem. Int x [] = False elem. Int x (y: ys) = (x ==Int y) || elem. Int x ys © M. Winter 10. 18

COSC 2 P 05 – Programming languages Generalization may lead to the definition: elem. Gen : : (a -> Bool) -> a -> [a] -> Bool elem. Gen p x [] = False elem. Gen p x (y: ys) = p x y || elem. Gen x ys but this is too general in a sense, because it can be used with any parameter of type a -> Bool rather than just an equality check © M. Winter 10. 19

COSC 2 P 05 – Programming languages Classes A type class or simply a class defines a collection of types over which specific functions are defined. class Eq a where (==) : : a -> Bool Members of a class are called instances. Built-in instances of Eq include the base types Int, Float, Bool, Char, tuples and lists built from types which are themselves instances of Eq, e. g. , (Int, Bool) and [[Char]]. elem : : Eq a => a -> [a] -> Bool elem x [] = False elem x (y: ys) = (x == y) || elem x ys © M. Winter 10. 20

COSC 2 P 05 – Programming languages Instances of Classes instance Eq Bool True == True False == False _ == _ where = True = False instance (Eq a, Eq b) => Eq (a, b) where (x, y) == (z, w) = x==z && y==w © M. Winter 10. 21

COSC 2 P 05 – Programming languages List comprehension Suppose that the list ex is [2, 4, 7], then the list comprehension [ 2*n | n <- ex ] will result in [4, 8, 14]. Further examples: [ 2*n | n <- ex, even n, n > 3] = [8] [ m+n | (m, n) <- [(2, 3), (2, 1), (7, 8)] ] = [5, 3, 15] [ m+n | n <- ex, even n, m <- ex, odd m] = [9, 11] List comprehension is not a new feature of the language. Each expression using list comprehension can be translated into an expression of the core language, i. e. , without list comprehension. © M. Winter 10. 22