COS 423 Theory of Algorithms Princeton University Spring

COS 423: Theory of Algorithms Princeton University Spring, 2001 Kevin Wayne Princeton University • COS 423 • Theory of Algorithms • Spring 2002 • Kevin Wayne

Theory of Algorithms Algorithm. (webster. com) n n A procedure for solving a mathematical problem (as of finding the greatest common divisor) in a finite number of steps that frequently involves repetition of an operation. Broadly: a step-by-step procedure for solving a problem or accomplishing some end especially by a computer. "Great algorithms are the poetry of computation. " Etymology. n "algos" = Greek word for pain. n "algor" = Latin word for to be cold. n Abu Ja'far al-Khwarizmi's = 9 th century Arab scholar. – his book "Al-Jabr wa-al-Muqabilah" evolved into today's high school algebra text 2

Imagine: A World With No Algorithms Fast arithmetic. Cryptography. Quicksort. n Databases. FFT. n Signal processing. Huffman codes. n Data compression. Network flow. n Routing Internet packets. Linear programming. n n Planning, decision-making. 3

What is COS 423? Introduction to design and analysis of computer algorithms. n Algorithmic paradigms. n Analyze running time of programs. n Data structures. n Understand fundamental algorithmic problems. n Intrinsic computational limitations. n Models of computation. n Critical thinking. Prerequisites. n COS 226 (array, linked list, search tree, graph, heap, quicksort). n COS 341 (proof, induction, recurrence, probability). 4

Administrative Stuff Lectures: (Kevin Wayne) n Monday, Wednesday 10: 00 - 10: 50, COS 104. TA's: (Edith Elkind, Sumeet Sobti) Textbook: Introduction to Algorithms (CLR). Grading: n Weekly problem sets. n Collaboration, no-collaboration. n Class participation, staff discretion. n Undergrad / grad. Course web site: courseinfo. princeton. edu/courses/COS 423_S 2001/ n Fill out questionnaire. 5

Approximate Lecture Outline Algorithmic paradigms. n Divide-and-conquer. n Greed. n Dynamic programming. n Reductions. Analysis of algorithms. n Amortized analysis. Data structures. n Union find. n Search trees and extensions. Graph algorithms. n Shortest path, MST. n Max flow, matching. 6

Approximate Lecture Outline NP completeness. n More reductions. n Approximation algorithms. Other models of computation. n Parallel algorithms. n Randomized algorithms. Miscellaneous. n Numerical algorithms. n Linear programming. 7

College Admissions Sample problem. Algorithm. Analysis. References: The Stable Marriage Problem by Dan Gusfield and Robert Irving, MIT Press, 1989. Introduction to Algorithms by Jon Kleinberg and Éva Tardos. Princeton University • COS 423 • Theory of Algorithms • Spring 2002 • Kevin Wayne

College Admissions Goal: Design a self-reinforcing college admissions process. Given a set of preferences among colleges and applicants, can we assign applicants to colleges so that for every applicant X, and every college C that X is not attending, either: n n C prefers every one of its admitted students to X; X prefers her current situation to the situation in which she is attending college C. If this holds, the outcome is STABLE. n Individual self-interest prevents any applicant / college to undermine assignment by joint action. 9

Love, Marriage, and Lying Standard disclaimer. Princeton University • COS 423 • Theory of Algorithms • Spring 2002 • Kevin Wayne

Stable Matching Problem: Given N men and N women, find a "suitable" matching between men and women. n Participants rate members of opposite sex. n Each man lists women in order of preference from best to worst. Men’s Preference List Man 1 st 2 nd 3 rd 4 th 5 th Victor Bertha Amy Diane Erika Clare Wyatt Diane Bertha Amy Clare Erika Xavier Bertha Erika Clare Diane Amy Yancey Amy Diane Clare Bertha Erika Zeus Bertha Diane Amy Erika Clare best worst 11

Stable Matching Problem: Given N men and N women, find a "suitable" matching between men and women. n Participants rate members of opposite sex. n Each man lists women in order of preference from best to worst. n Each woman lists men in order of preference. Women’s Preference List Woman 1 st 2 nd 3 rd 4 th 5 th Amy Zeus Victor Wyatt Yancey Xavier Bertha Xavier Wyatt Yancey Victor Zeus Clare Wyatt Xavier Yancey Zeus Victor Diane Victor Zeus Yancey Xavier Wyatt Erika Yancey Wyatt Zeus Xavier Victor best worst 12

Stable Matching Problem: Given N men and N women, find a "suitable" matching between men and women. n n PERFECT MATCHING: everyone is matched monogamously. – each man gets exactly one woman – each woman gets exactly one man STABILITY: no incentive for some pair of participants to undermine assignment by joint action. – in matching M, an unmatched pair (m, w) is UNSTABLE if man m and woman w prefer each other to current partners – unstable pair could each improve by dumping spouses and eloping STABLE MATCHING = perfect matching with no unstable pairs. (Gale and Shapley, 1962) 13

Example Men’s Preference List Women’s Preference List Man 1 st 2 nd 3 rd Woman 1 st 2 nd 3 rd Xavier A B C Amy Y X Z Yancey B A C Bertha X Y Z Zeus A B C Clare X Y Z Lavender assignment is a perfect matching. Are there any unstable pairs? ! Yes. Bertha and Xavier form an unstable pair. They would prefer each other to current partners. 14

Example Men’s Preference List Women’s Preference List Man 1 st 2 nd 3 rd Woman 1 st 2 nd 3 rd Xavier A B C Amy Y X Z Yancey B A C Bertha X Y Z Zeus A B C Clare X Y Z Green assignment is a stable matching. 15

Example Men’s Preference List Women’s Preference List Man 1 st 2 nd 3 rd Woman 1 st 2 nd 3 rd Xavier A B C Amy Y X Z Yancey B A C Bertha X Y Z Zeus A B C Clare X Y Z Orange assignment is also a stable matching. 16

Stable Roommate Problem Not obvious that any stable matching exists. Consider related "stable roommate problem. " n 2 N people. n Each person ranks others from 1 to 2 N-1. n Assign roommate pairs so that no unstable pairs. Preference List 1 st 2 nd 3 rd Adam B C D Bob C A D Chris A B D Doofus A B C All 3 perfect matchings have unstable pair. E. g. , A-C forms unstable pair in lavender matching. No stable matching. 17

Propose-And-Reject Algorithm Intuitive method that guarantees to find a stable matching. Gale-Shapley Algorithm (men propose) Initialize each person to be free. while (some man m is free and hasn't proposed to every woman) w = first woman on m's list to whom m has not yet proposed if (w is free) assign m and w to be engaged else if (w prefers m to her fiancé m') assign m and w to be engaged, and m' to be free else w rejects m 18

Implementation and Running Time Analysis Engagements. n n Maintain two arrays wife[m], and husband[w]; set equal to 0 if participant is free. Store list of free men on a stack (queue). Preference lists. n n For each man, create a linked list of women, ordered from favorite to worst. – men propose to women at top of list, if rejected goto next For each woman, create a "ranking array" such that mth entry in array is woman's ranking of man m. – allows for queries of the form: does woman w prefer m to m' ? Resource consumption. n Time = (N 2). n Space = (N 2). n Optimal. 19

A Worst Case Instance Number of proposals n(n-1) + 1. n Algorithm terminates when last woman gets first proposal. Number of proposals = n(n-1) + 1 for following family of instances. Men's Preference List Women's Preference List Man 1 st 2 nd 3 rd 4 th 5 th Victor A B C D E Amy W X Y Z V Wyatt B C D A E Bertha X Y Z V W Xavier C D A B E Clare Y Z V W X Yancey D A B C E Diane Z V W X Y Zeus A B C D E Erika V W X Y Z 20

Proof of Correctness Observation 1. Men propose to their favorite women first. Observation 2. Once a woman is matched, she never becomes unmatched. She only "trades up. " Fact 1. All men and women get matched (perfect). Suppose upon termination Zeus is not matched. Then some woman, say Amy, is not matched upon termination. By Observation 2, Amy was never proposed to. But, Zeus proposes to everyone, since he ends up unmatched. (contradiction) n n 21

Proof of Correctness Observation 1. Men propose to their favorite women first. Observation 2. Once a woman is matched, she never becomes unmatched. She only "trades up. " Fact 2. No unstable pairs. Suppose (Amy, Zeus) is an unstable pair: each prefers each other to partner in Gale-Shapley matching S*. n n n Case 1. Zeus never proposed to Amy. Þ Zeus must prefer Bertha to Amy (Observation 1) Þ (Amy, Zeus) is stable. (contradiction) S* Amy-Yancey Bertha-Zeus Case 2. Zeus proposed to Amy. Þ Amy rejected Zeus (right away or later) Þ Amy prefers Yancey to Zeus (women only trade up) Þ (Amy, Zeus) is stable (contradiction) 22

Understanding the Solution For a given problem instance, there may be several stable matchings. n Do all executions of Gale-Shapley yield the same stable matching? If so, which one? Fact 3. Yes. Gale-Shapley finds MAN-OPTIMAL stable matching! n n Man m is a valid partner of woman w if there exists some stable matching in which they are married. Man-optimal assignment: every man receives best valid partner. – simultaneously best for each and every man – there is no stable matching in which any single man individually does better 23

Proof of Fact 3 Proof. n n n Suppose, for sake of contradiction, some man is paired with someone other than best partner. – since men propose in decreasing order of preference, some man is rejected by valid partner S Amy-Yancey Bertha-Zeus Let Yancey be first such man, and let Amy be first valid partner that rejects him. When Yancey is rejected, Amy forms (or reaffirms) engagement with man, say Zeus, whom she prefers to Yancey. Let Bertha be Zeus' partner in S. Zeus not rejected by any valid partner at the point when Yancey is rejected by Amy (since Yancey is first to be rejected by valid partner). Thus, Zeus prefers Amy to Bertha. n But Amy prefers Zeus to Yancey. n Thus (Amy, Zeus) is unstable pair in S. 24

Understanding the Solution Fact 4. Gale-Shapley finds WOMAN-PESSIMAL matching. n Each woman married to worst valid partner. – simultaneously worst for each and every woman. – there is no stable matching in which any single woman individually does worse Proof. n n Suppose (Amy, Zeus) matched in S*, but Zeus is not worst valid partner for Amy. There exists stable matching S in which Amy is paired with man, say Yancey, whom she likes less than Zeus. n Let Bertha be Zeus' partner in S. n Zeus prefers Amy to Bertha (man optimality). n (Amy, Zeus) form unstable pair in S. S Amy-Yancey Bertha-Zeus 25

Understanding the Solution Fact 5. The man-optimal stable matching is weakly Pareto optimal. n There is no other perfect matching (stable or unstable), where every man does strictly better. Proof. n n n Let Amy be last woman in some execution of Gale-Shapley (men propose) algorithm to receive a proposal. No man is rejected by Amy since algorithm terminates when last woman receives first proposal. No man matched to Amy will be strictly better off than in manoptimal stable matching. 26

Extensions: Unacceptable Partners Yeah, but in real-world every woman is not willing to marry every man, and vice versa? n n Some participants declare others as "unacceptable. " (prefer to be alone than with given partner) Algorithm extends to handle partial preference lists. Matching S unstable if there exists man m and woman w such that: n m is either unmatched in S, or strictly prefers w to his partner in S n w is either unmatched in S, or strictly prefers m to her partner in S. Fact 6. Men and women are each partitioned into two sets: n those that have partners in all stable matchings; n those that have partners in none. 27

Extensions: Sets of Unequal Size Also, there may be an unequal number of men and women. n E. g. , |M| = 100 men, |W| = 90 women. n Algorithm extends. n WLOG, assume |W| < |M|. Matching S unstable if there exists man m and woman w such that: n m is either unmatched in S, or strictly prefers w to his partner in S; n w is either unmatched in S, or strictly prefers m to her partner in S. Fact 7. All women are matched in every stable matching. Men are partitioned into two subsets: n men who are matched in every stable matching; n men who are matched in none. 28

Extensions: Limited Polygamy What about limited polygamy? n E. g. , Bill wants 3 women. n Algorithm extends. Matching S unstable if there exists man m and woman w such that: n n either w is unmatched, or w strictly prefers m to her partner; either m does not have all its "places" filled in the matching, or m strictly prefers w to at least one of its assigned residents. 29

Application: Matching Residents to Hospitals Sets of unequal size, unacceptable partners, limited polygamy. Matching S unstable if there exists hospital h and resident r such that: n h and r are acceptable to each other; n either r is unmatched, or r prefers h to her assigned hospital; n either h does not have all its places filled in the matching, or h prefers r to at least one of its assigned residents. 30

Application: Matching Residents to Hospitals Matching medical school residents to hospitals. (NRMP) n Hospitals ~ Men (limited polygamy allowed). n Residents ~ Women. n Original use just after WWII (predates computer usage). n Ides of March, 13, 000+ residents. Rural hospital dilemma. n Certain hospitals (mainly in rural areas) were unpopular and declared unacceptable by many residents. n Rural hospitals were under-subscribed in NRMP matching. n How can we find stable matching that benefits "rural hospitals"? Rural Hospital Theorem: ! Rural hospitals get exactly same residents in every stable matching! 31

Deceit: Machiavelli Meets Gale-Shapley Is there any incentive for a participant to misrepresent his/her preferences? n Assume you know men’s propose-and-reject algorithm will be run. n Assume that you know the preference lists of all other participants. Fact 8. No, for any man yes, for some women! Men’s Preference List Women’s True Preference List Man 1 st 2 nd 3 rd Woman 1 st 2 nd 3 rd Xavier A B C Amy Y X Z Yancey B A C Bertha X Y Z Zeus A B C Clare X Y Z Amy Lies Woman 1 st 2 nd 3 rd Amy Y Z X Bertha X Y Z Clare X Y Z 32

Lessons Learned Powerful ideas learned in COS 423. n Isolate underlying structure of problem. n Create useful and efficient algorithms. n Sometimes deep social ramifications. ! Historically, men propose to women. Why not vice versa? ! Men: propose early and often. ! Men: be more honest. ! Women: ask out the guys. ! Theory can be socially enriching and fun! ! CS majors get the best partners!!! 33

Love, Marriage, and Lying: Extra Slides Princeton University • COS 423 • Theory of Algorithms • Spring 2002 • Kevin Wayne

Example With a Unique Stable Matching Men’s Preference List Women’s Preference List Man 1 st 2 nd 3 rd Woman 1 st 2 nd 3 rd Xavier B A C Amy Y Z X Yancey B C A Bertha Z X Y Zeus C B A Clare Y X Z Red matching is unique stable matching. 35

How to Represent Men and Women Represent men and women as integers between 0 and N-1. n n 0 through N-1 since C array indices start at 0. Could use struct if we want to carry around more information, e. g. , name, age, astrological sign. 36

How to Represent Marriages Use array to keep track of marriages. int wife[N]; int husb[N]; for (m = 0; m < N; m++) wife[m] = -1; for (w = 0; w < N; w++) husb[w] = -1; 37

Filling in Some of the Code while (marriages < N) find unmatched man while (m unmatched) if (w unmatched) m and w get engaged m' = current fiancé of w m' now unmatched m and w get engaged for (m = 0; wife[m] != -1; m++) ; while (-1 == wife[m]) let w be man m’s favorite women to whom he has not yet proposed if (-1 == husb[w]) husb[m] = w; wife[w] = m; marriages++; else if (w prefers m to current fiancé) m' = husb[w]; wife[m'] = -1; husb[m] = w; wife[w] = m; 38

Representing the Preference Lists Use 2 D-array to represent preference lists. n n n 2 D-array is array of arrays. mp[m][i] = w if man m’s ith favorite woman is w. wp[w][i] = m if woman w’s ith favorite man is m. mp[1][0] = 3 man 1 likes woman 3 the best int mp[N][N]; int wp[N][N]; 39

Initializing the Preference Lists Could read from stdin. We’ll assign random lists for each man and woman. Use random. Permutation function from Lecture P 2. n n Need N random permutations for men, and N for women. int mp[N][N]; int wp[N][N]; for (m = 0; m < N; m++) random. Permutation(mp[m], N); mp[m] is man m’s preference list array. for (w = 0; w < N; w++) random. Permutation(wp[w], N); 40

Dumping Does woman w=2 prefer man m 1=3 to man m 2=0? ! Yes, m 1 appears on woman w’s preference list before m 2. search preference list sequentially until m 1 or m 2 found for (i = 0; i < N; i++) { if (wp[w][i] == m 1) YES if (wp[w][i] == m 2) NO } 41

Keeping Track of Men’s Proposals Unmatched man proposes to most favorable woman to whom he hasn’t already proposed. How do we keep track of which woman a man has proposed to? n n Men propose in decreasing order of preference. Suffices to keep track of number of proposals in array. propose[m] = i if man m has proposed to i woman already. initialize array int props[N]; for (i = 0; i < N; i++) props[i] = 0; 42

Keeping Track of Men’s Proposals Unmatched man proposes to most favorable woman to whom he hasn’t already proposed. How do we keep track of which woman a man has proposed to? n n Men propose in decreasing order of preference. Suffices to keep track of number of proposals in array. propose[m] = i if man m has proposed to i woman already. find next woman to propose to while (-1 == wife[n]) { w = mp[m][props[m]]; props[m]++; . . . } props[m] is ranking of next woman on preference list make next proposal to woman mp[m][props[m]] 43

Try Out The Code marriage. c #include <stdio. h> #include <stdlib. h> #include <assert. h> #define N 500 int main(void) { int mp[N][N]; int wife[N]; int husb[N]; int props[N]; /* /* /* int marriages = 0; int m, w; mp[m][i] wp[w][i] wife[m] husb[w] props[m] = = = w m i if if if man m's ith favorite woman is w */ woman w's ith favorite man is m */ m married to w */ man m has proposed to i women */ /* number of couples matched so far */ /* initialize men */ for (m = 0; m < N; m++) { props[m] = 0; wife[m] = -1; random. Permutation(mp[m], N); } /* initialize women */ for (w = 0; w < N; w++) { husb[w] = -1; random. Permutation(wp[w], N); } 44

Try Out The Code marriage. c while (marriages < N) { /* find first unmatched man */ for (m = 0; wife[m] != -1; m++) ; printf("man %d proposing: n", m); /* propose to next women on list until successful */ while (-1 == wife[m]) { w = mp[m][props[m]]; printf(" to woman %d", w); props[m]++; /* woman w unmatched */ if (-1 == husb[w]) { printf(" acceptedt(woman %d previously unmatched)n", w); husb[w] = m; wife[m] = w; marriages++; } /* woman w prefers m to current mate */ else if (wr[w][m] < wr[w][husb[w]]) { printf(" acceptedt(woman %d dumps man %d)n", w, husb[w]); wife[husb[w]] = -1; husb[w] = m; wife[m] = w; } /* otherwise m rejected by w */ else printf(" rejectedt(woman %d prefers %d)n", w, husb[w]); } } 45

Try Out The Code Unix marriage. c printf("Stable matchingn"); for (m = 0; m < N; m++) printf("%5 d %5 dn", m, wife[m]); return 0; } Observation: code is REALLY slow for large N. % gcc marriage. c % a. out man 0 proposing: to woman 4 accepted man 1 proposing: to woman 0 accepted man 2 proposing: to woman 2 accepted man 3 proposing: to woman 2 rejected to woman 3 accepted man 4 proposing: to woman 2 accepted man 2 proposing: to woman 3 accepted man 3 proposing: to woman 0 rejected to woman 4 rejected to woman 1 accepted (woman 4 previously unmatched) (woman 0 previously unmatched) (woman 2 prefers 2) (woman 3 previously unmatched) (woman 2 dumps man 2) (woman 3 dumps man 3) (woman 0 prefers 1) (woman 4 prefers 0) (woman 1 previously unmatched) Stable matching 0 4 1 0 2 3 3 1 4 2 46

Why So Slow? Does woman w=2 prefer man m 1=3 to man m 2=0? ! Need to search through row 2 to find answer. This is repeated many times. If N is large, this can be very expensive. 47

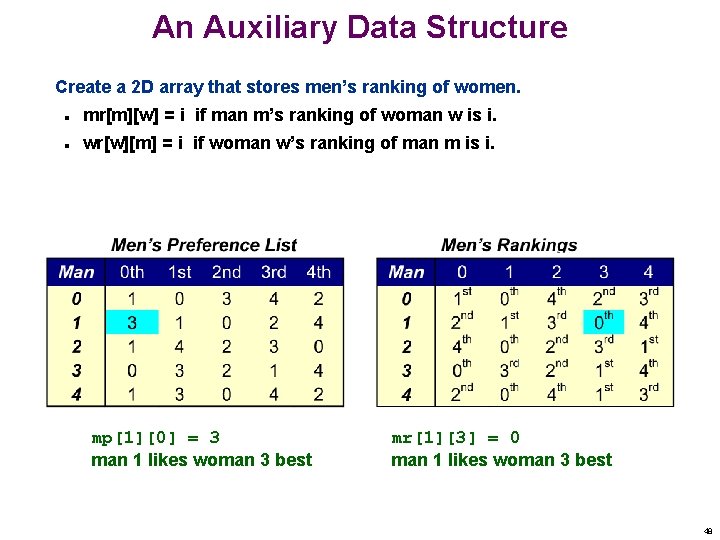
An Auxiliary Data Structure Create a 2 D array that stores men’s ranking of women. n mr[m][w] = i if man m’s ranking of woman w is i. n wr[w][m] = i if woman w’s ranking of man m is i. mp[1][0] = 3 man 1 likes woman 3 best mr[1][3] = 0 man 1 likes woman 3 best 48

An Auxiliary Data Structure Create a 2 D array that stores men’s ranking of women. n mr[m][w] = i if man m’s ranking of woman w is i. n wr[w][m] = i if woman w’s ranking of man m is i. Does man m = 3 prefer woman w 1 = 2 to woman w 2 = 4? if (mr[m][w 1] < mr[m][w 2]) YES else NO mr[m][w 1] = 2 mr[m][w 2] = 4 49

Check if Marriage is Stable Check if husb[N] and wife[N] correspond to a stable marriage. n Good warmup and useful for debugging. n Check every man-woman pair to see if they’re unstable. n Use ranking arrays. is. Stable int is. Stable(int husb[], int wife[], int mr[N][N], int wr[N][N]) { int m, w; for (m = 0; m < N; m++) for (w = 0; w < N; w++) if (mr[m][w] < mr[m][wife[m]]) && (wr[w][m] < wr[w][husb[w]]) return 0; return 1; w prefers m to current husband } m prefers w to current wife 50

Check if Marriage is Stable Check if husb[N] and wife[N] correspond to a stable marriage. n Good warmup and useful for debugging. n Check every man-woman pair to see if they’re unstable. n Use ranking arrays. Time/space tradeoff for using auxiliary ranking arrays. n n Disadvantage: requires twice as much memory (storage). Advantage: dramatic speedup in running time (using 400 MHz Pentium II with N = 10, 000). ! 1 second using ranking arrays. ! 2 hours by searching preference list sequentially! 51