Correlation tests Correlation Coefficient A succinct measure of










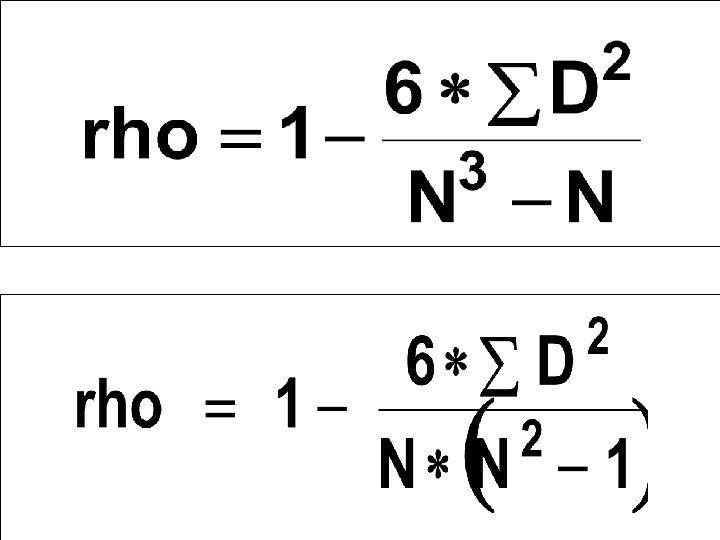





- Slides: 25

Correlation tests:

Correlation Coefficient: A succinct measure of the strength of the relationship between two variables (e. g. height and weight, age and reaction time, IQ and exam score).

There are various types of correlation coefficient, for different purposes: 1. Pearson's "r": Used when both X and Y variables are (a) continuous; (b) (ideally) measurements on interval or ratio scales; (c) normally distributed - e. g. height, weight, IQ. 2. Spearman's rho: In same circumstances as (1), except that data need only be on an ordinal scale - e. g. attitudes, personality scores.

r is a parametric test: the data have to have certain characteristics (parameters) before it can be used. rho is a non-parametric test - less fussy about the nature of the data on which it is performed.

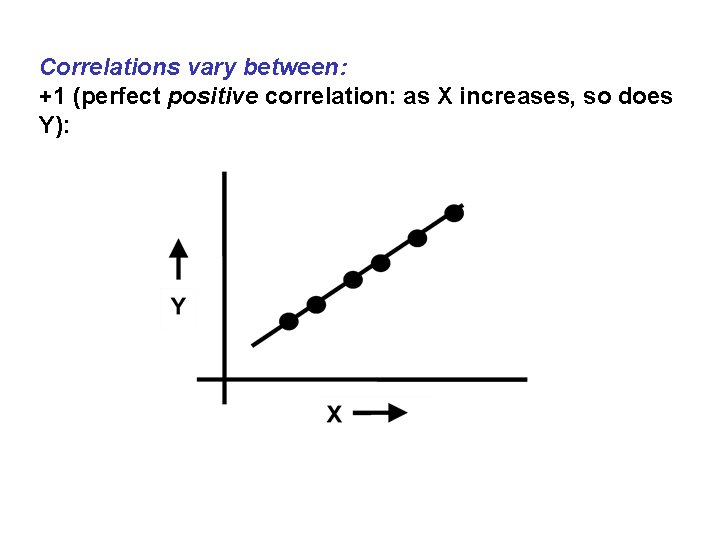
Correlations vary between: +1 (perfect positive correlation: as X increases, so does Y):

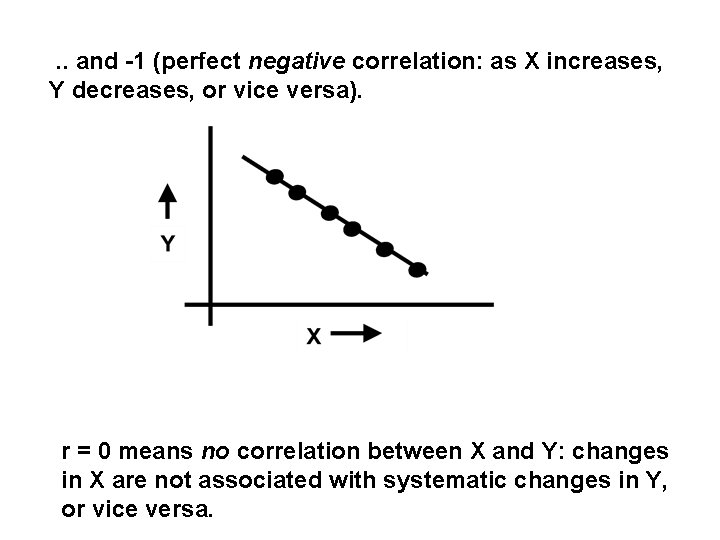
. . . and -1 (perfect negative correlation: as X increases, Y decreases, or vice versa). r = 0 means no correlation between X and Y: changes in X are not associated with systematic changes in Y, or vice versa.

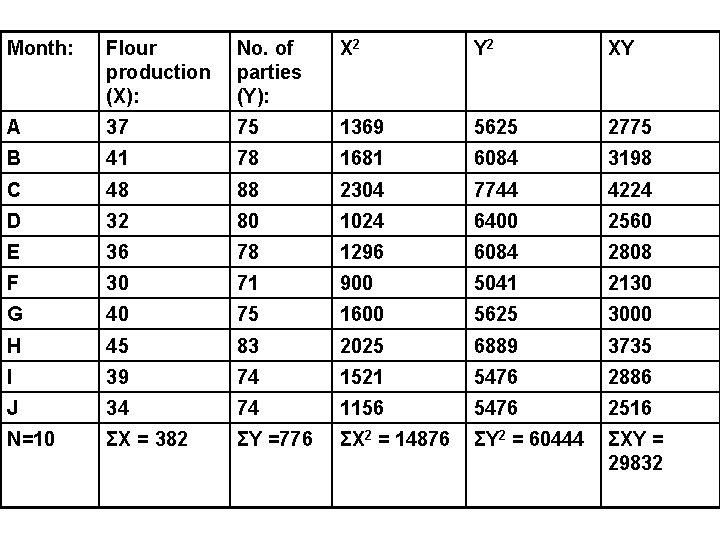
Calculating Pearson's r: a worked example: Is there a relationship between the number of parties a person gives each month, and the amount of flour they purchase from Vinny Millar?

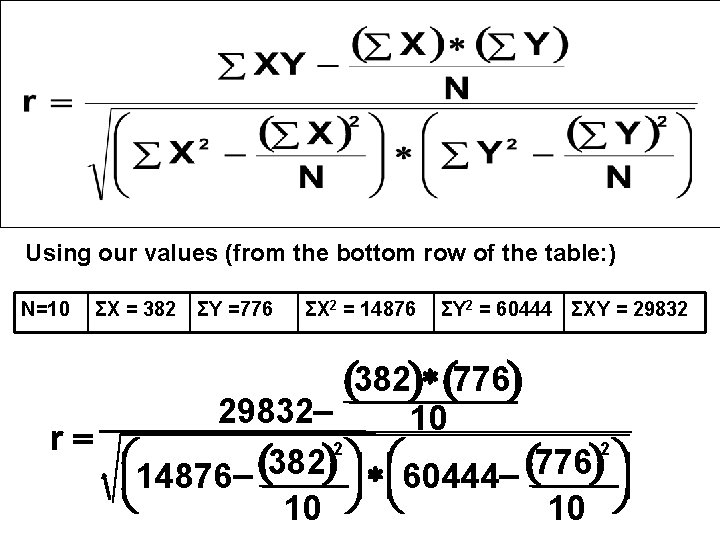
Month: Flour production (X): No. of parties (Y): X 2 Y 2 XY A 37 75 1369 5625 2775 B 41 78 1681 6084 3198 C 48 88 2304 7744 4224 D 32 80 1024 6400 2560 E 36 78 1296 6084 2808 F 30 71 900 5041 2130 G 40 75 1600 5625 3000 H 45 83 2025 6889 3735 I 39 74 1521 5476 2886 J 34 74 1156 5476 2516 N=10 ΣX = 382 ΣY =776 ΣX 2 = 14876 ΣY 2 = 60444 ΣXY = 29832

Using our values (from the bottom row of the table: ) N=10 ΣX = 382 ΣY =776 ΣX 2 = 14876 ΣY 2 = 60444 ΣXY = 29832 (382)* (776) 2983210 r= 2 2 æç ö æ ö 382 776 ( ) ÷÷ * çç 60444÷÷ çè 1487610 ø è 10 ø

29832 - 29643. 20 r= (14876 - 14592. 40)* (60444 - 60217. 60) 188. 80 r= 283. 60 * 226. 40 = 188. 80 =. 7455 253. 391 r is. 75. This is a positive correlation: people who buy a lot of flour from Vinny Millar also hold a lot of parties (and vice versa).

How to interpret the size of a correlation: r 2 is the "coefficient of determination". It tells us what proportion of the variation in the Y scores is associated with changes in X. e. g. , if r is. 2, r 2 is 4% (. 2 *. 2 = . 04 = 4%). Only 4% of the variation in Y scores is attributable to Y's relationship with X. Thus, knowing a person's Y score tells you essentially nothing about what their X score might be.

Our correlation of. 75 gives an r 2 of 56%. An r of. 9, gives an r 2 of (. 9 *. 9 =. 81) = 81%. Note that correlations become much stronger the closer they are to 1 (or -1). Correlations of. 6 or -. 6 (r 2 = 36%) are much better than correlations of. 3 or -. 3 (r 2 = 9%), not merely twice as strong!

Spearman's rho: Measures the degree of monotonicity rather than linearity in the relationship between two variables - i. e. , the extent to which there is some kind of change in X associated with changes in Y: Hence, copes better than Pearson's r when the relationship is monotonic but non-linear - e. g. :

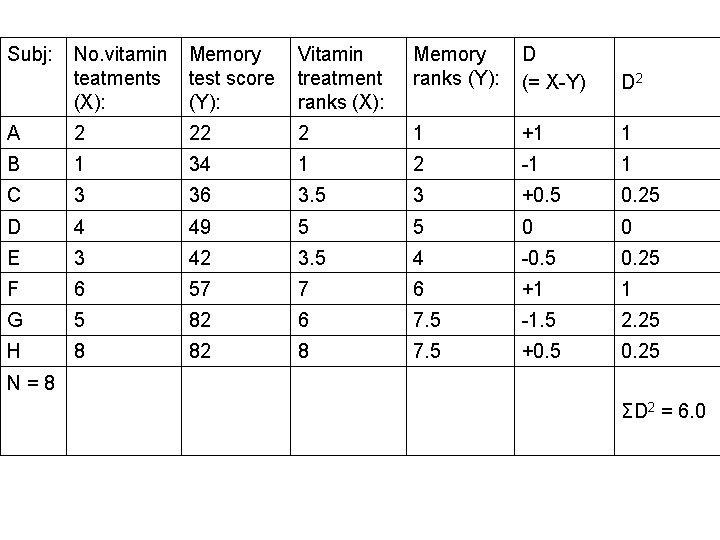
Spearman's rho - worked example: Is there a correlation between the number of vitamin treatments a person has, and their score on a memory test?

Subj: No. vitamin teatments (X): Memory test score (Y): Vitamin treatment ranks (X): Memory ranks (Y): D (= X-Y) D 2 A 2 22 2 1 +1 1 B 1 34 1 2 -1 1 C 3 36 3. 5 3 +0. 5 0. 25 D 4 49 5 5 0 0 E 3 42 3. 5 4 -0. 5 0. 25 F 6 57 7 6 +1 1 G 5 82 6 7. 5 -1. 5 2. 25 H 8 82 8 7. 5 +0. 5 0. 25 N=8 ΣD 2 = 6. 0
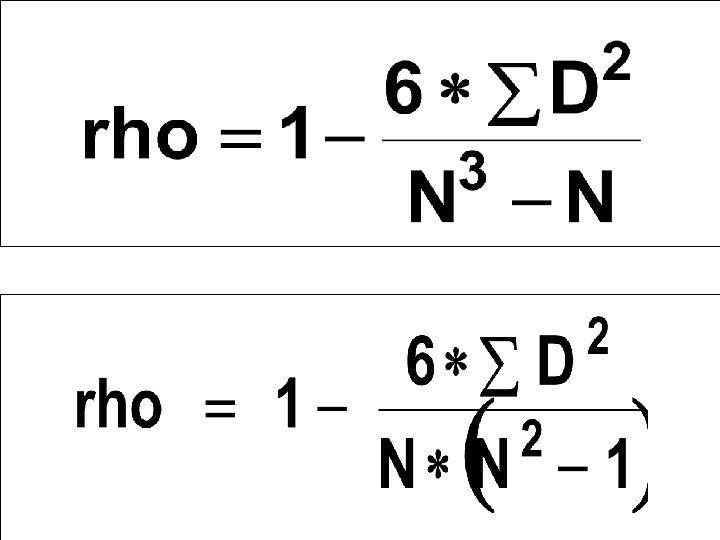
OR

Step 1: assign ranks to the raw data, for each variable separately. Rules for ranking: (a) Give the lowest score a rank of 1; next lowest a rank of 2; etc. (b) If two or more scores are identical, this is a "tie": give them the average of the ranks they would have obtained had they been different. The next score that is different, gets the rank it would have had if the tied scores had not occurred.

e. g. : raw score "original"rank actual rank: 12 1 1 15 2 2. 5 15 3 2. 5 16 4 4 17 5 5 Rank for the tied scores is (2+3)/2 = 2. 5 raw score "original"rank actual rank: 3 1 1 18 2 3 18 3 3 18 4 3 Rank for the tied scores is (2+3+4)/3 = 3 100 5 5

Step 2: Subtract one set of ranks from the other, to get a set of differences, D. Step 3: Square each of these differences, to get D 2. Step 4: Add up the values of D 2 , to get ΣD 2. Here, ΣD 2 = 6. 0 N = 8.

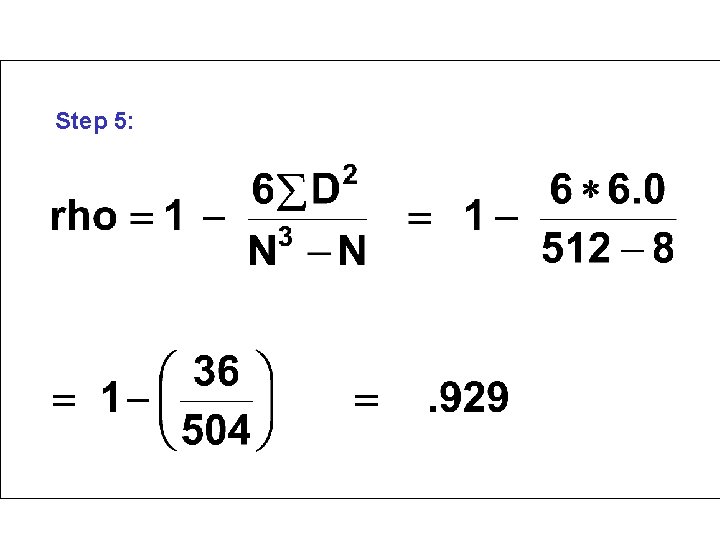
Step 5:

rho =. 93. There is a strong positive correlation between the number of vitamin treatments a person has, and their memory test score. Pearson's r on the same data =. 86.

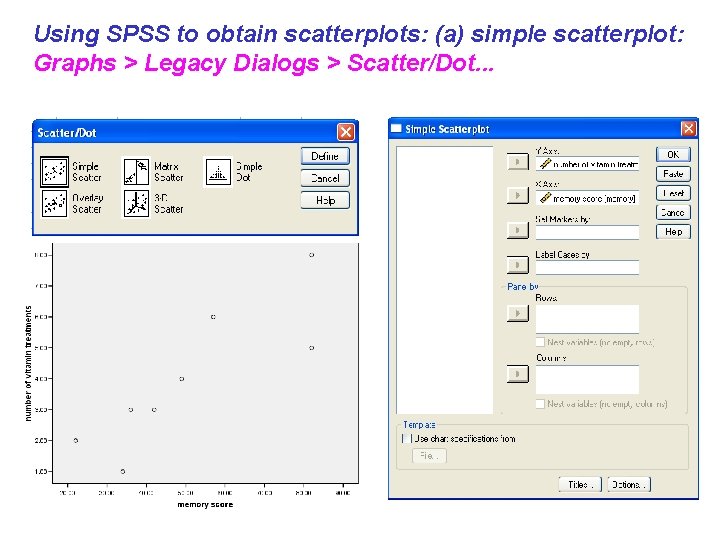
Using SPSS to obtain scatterplots: (a) simple scatterplot: Graphs > Legacy Dialogs > Scatter/Dot. . .

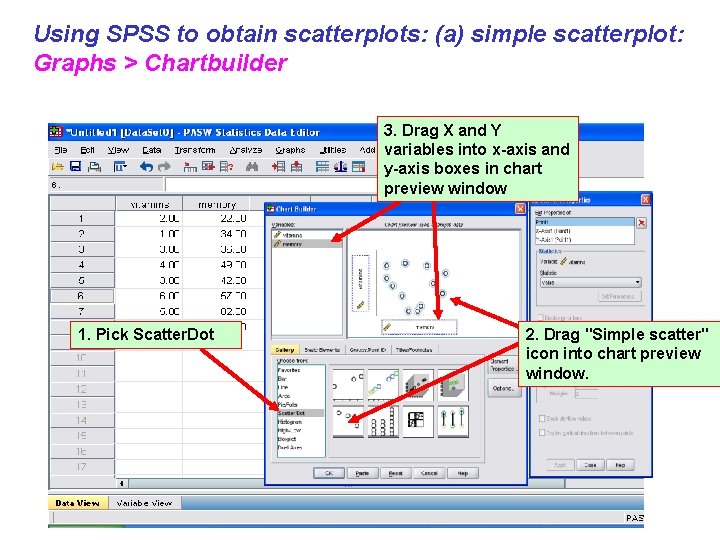
Using SPSS to obtain scatterplots: (a) simple scatterplot: Graphs > Chartbuilder 3. Drag X and Y variables into x-axis and y-axis boxes in chart preview window 1. Pick Scatter. Dot 2. Drag "Simple scatter" icon into chart preview window.

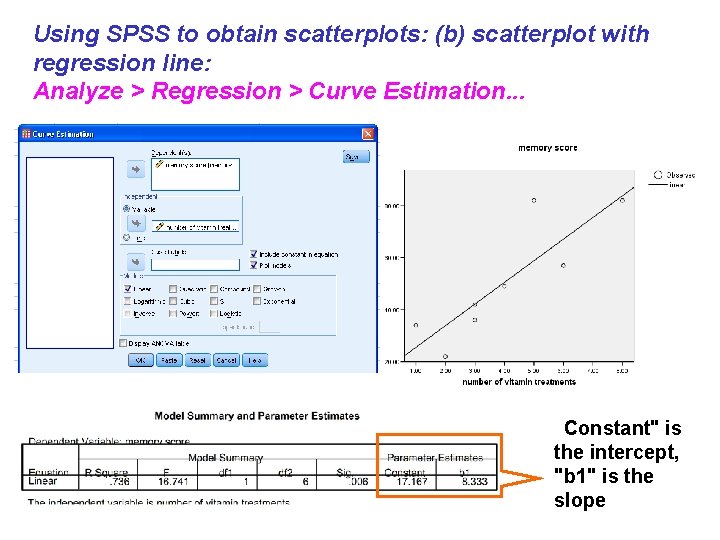
Using SPSS to obtain scatterplots: (b) scatterplot with regression line: Analyze > Regression > Curve Estimation. . . "Constant" is the intercept, "b 1" is the slope

Using SPSS to obtain correlations: Analyze > Correlate > Bivariate. . .
 Elaborate/succinct communication style
Elaborate/succinct communication style What is a descriptive title
What is a descriptive title Ace different tests help iq tests
Ace different tests help iq tests Product moment correlation coefficient
Product moment correlation coefficient Interprétation de coefficient de corrélation
Interprétation de coefficient de corrélation Correlation coefficient google sheets
Correlation coefficient google sheets Intraclass correlation coefficient
Intraclass correlation coefficient Intraclass correlation excel
Intraclass correlation excel Pearson correlation method
Pearson correlation method R squared vs correlation coefficient
R squared vs correlation coefficient Spearman's rank correlation coefficient
Spearman's rank correlation coefficient Correlation and regression
Correlation and regression Intraclass correlation excel
Intraclass correlation excel Calculate correlation coefficient in excel
Calculate correlation coefficient in excel Correlation coefficient
Correlation coefficient Absolute value of correlation coefficient
Absolute value of correlation coefficient Properties of correlation coefficient
Properties of correlation coefficient Correlation coefficient method
Correlation coefficient method Null hypothesis for correlation
Null hypothesis for correlation Coefficient of correlation
Coefficient of correlation Multiple correlation coefficient formula
Multiple correlation coefficient formula Difference between regression and correlation
Difference between regression and correlation Correlation coefficient in analytical chemistry
Correlation coefficient in analytical chemistry How to find the correlation coefficient
How to find the correlation coefficient Correlation coefficient in analytical chemistry
Correlation coefficient in analytical chemistry Absolute value of correlation coefficient
Absolute value of correlation coefficient