CORRELATION Essentials Definitions Scatter Plots Correlation Types Correlation

CORRELATION • • Essentials Definitions Scatter Plots Correlation Types Correlation Coefficient, r Characteristics of r Steps Leading to r Hypotheses – Null & Alternative Is there a relationship between the lengths of body parts?

The invalid assumption that correlation implies cause is probably among the two or three most serious and common errors of human reasoning. --Stephen Jay Gould, The Mismeasure of Man Linear Correlation & Regression

Essentials: Correlation (The invalid assumption that correlation implies cause is probably among the two or three most serious and common errors of human reasoning. --Stephen Jay Gould, The Mismeasure of Man. ) n Correlation – potential relationships, not causality. n Know the steps one might employ before obtaining a correlation. n Know the characteristics of the Pearson Product Moment Correlation Coefficient (for us the correlation). n Be able to calculate a correlation and determine if it is statistically significant. n Be able to create a scatter plot of the paired data being studied. n Be able to determine the directionality of a correlation and its strength via formula and observation of plotted data.

Correlation n Correlation – A correlation exists between two variables when one of them is related to the other in some way. Paired Data – A measurement on two variables for each unit in a population or sample. Scatterplot – a graph in which the paired (x, y) data are plotted with a horizontal x-axis (independent variable) and a vertical y-axis (dependent variable). Each individual pair is plotted as a single point.

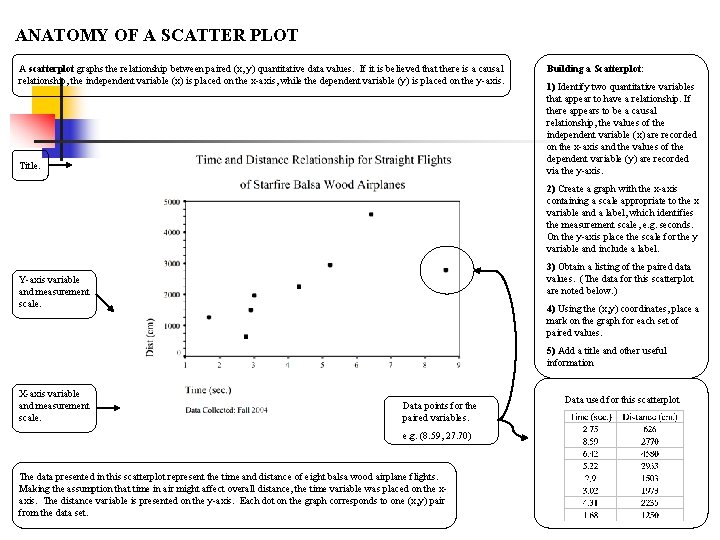
ANATOMY OF A SCATTER PLOT A scatterplot graphs the relationship between paired (x, y) quantitative data values. If it is believed that there is a causal relationship, the independent variable (x) is placed on the x-axis, while the dependent variable (y) is placed on the y-axis. Title. Building a Scatterplot: 1) Identify two quantitative variables that appear to have a relationship. If there appears to be a causal relationship, the values of the independent variable (x) are recorded on the x-axis and the values of the dependent variable (y) are recorded via the y-axis. 2) Create a graph with the x-axis containing a scale appropriate to the x variable and a label, which identifies the measurement scale, e. g. seconds. On the y-axis place the scale for the y variable and include a label. 3) Obtain a listing of the paired data values. (The data for this scatterplot are noted below. ) Y-axis variable and measurement scale. 4) Using the (x, y) coordinates, place a mark on the graph for each set of paired values. 5) Add a title and other useful information X-axis variable and measurement scale. Data points for the paired variables. e. g. (8. 59, 27. 70) The data presented in this scatterplot represent the time and distance of eight balsa wood airplane flights. Making the assumption that time in air might affect overall distance, the time variable was placed on the xaxis. The distance variable is presented on the y-axis. Each dot on the graph corresponds to one (x, y) pair from the data set. Data used for this scatterplot

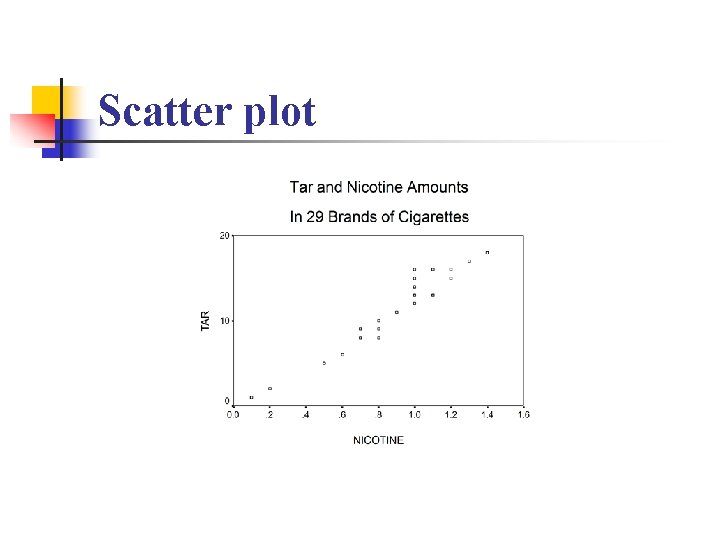
Scatter plot

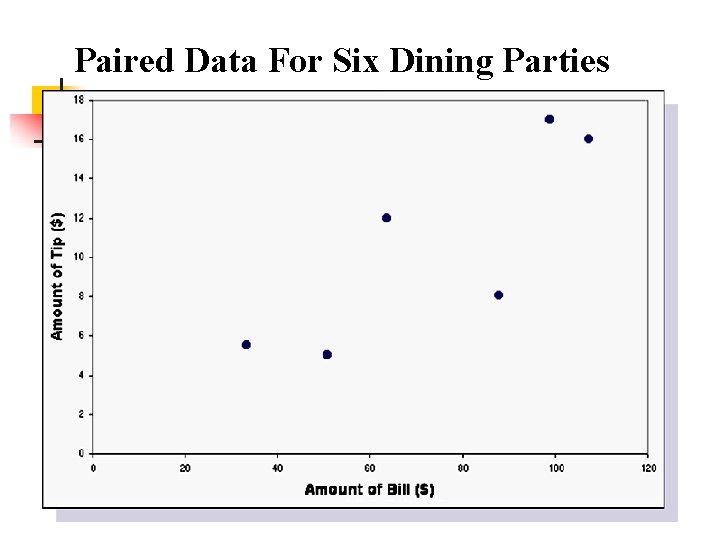
Paired Data For Six Dining Parties

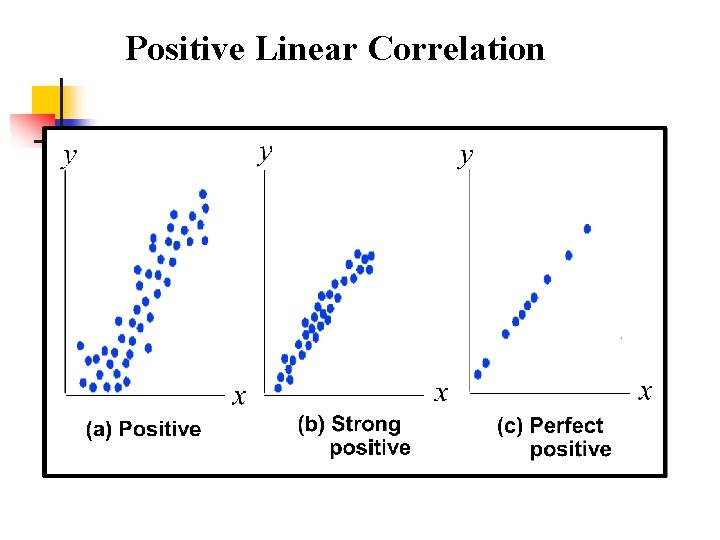
Positive Linear Correlation

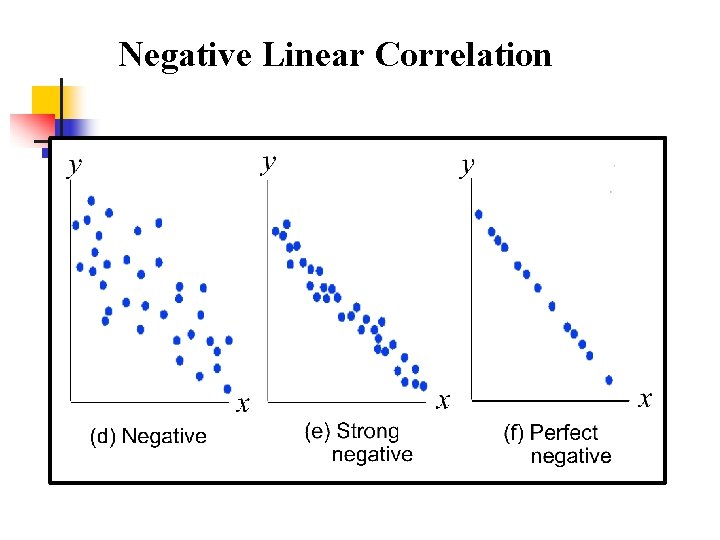
Negative Linear Correlation

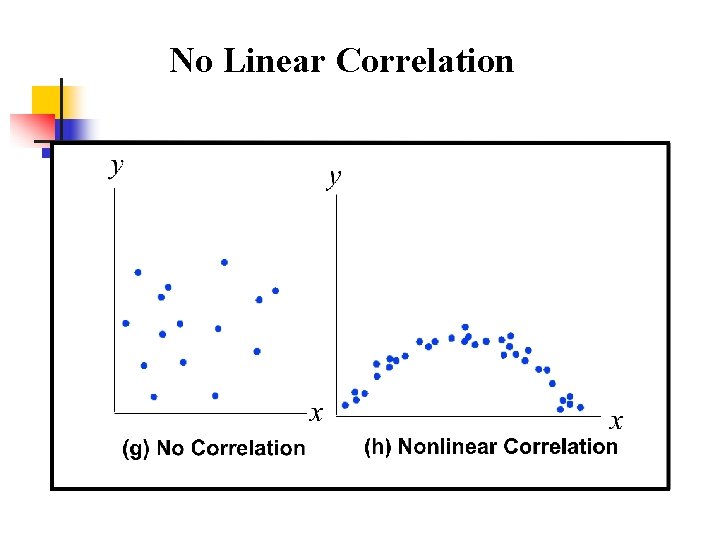
No Linear Correlation

The Linear Correlation Coefficient n n Denoted r when considering a sample, and (rho) when considering a population. The Linear Correlation Coefficient is a measure of direction and magnitude between the paired x and y values in a sample. Its value is obtained using the following formula:

Facts About r n n The value of r is always between – 1 and 1. The sign (-/+) of r reflects the direction of the correlation. n n If r is negative, then there exists a negative association between the two variables. That is, as one increases, the other decreases. If r is positive, then there exists a positive relationship between the two variables. That is, as one increases, the other increases.

Facts About r (cont. ) n The magnitude of the correlation indicates the strength of the association. Values closer to – 1 and 1 signify a stronger association n n A value of – 1 is a perfect negative correlation. A value of 1 is a perfect positive correlation.

Facts About r (cont. ) n n The value of r does not change if all values of either variable are converted to a different scale. The value of r is not affected by the choice of x and y. That is, if x and y are interchanged, the value of r will not change.

Does a Correlation Actually Exist? n n n The answer to this can be somewhat subjective. How strong does a correlation need to be? Start by asking the following: n n n Does it make sense to look at this relationship? Does a scatter plot present a relationship (either positive or negative)? If yes to both, calculate r.

We Begin With a Hypothesis n n In linear correlation, the null hypothesis states that no linear correlation exists. In other words, r = 0. [rho = 0] In notation The alternative hypothesis states that a linear correlation does exist. In other words r 0. [rho 0] In notation

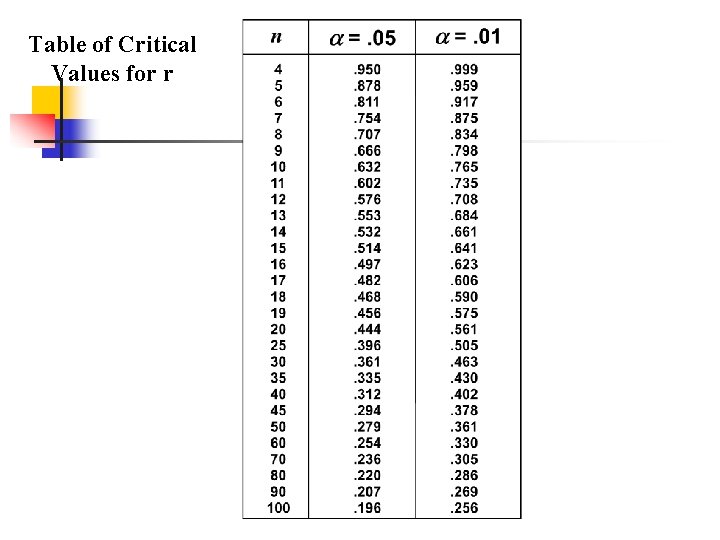
We Test The Hypothesis n n Based on the sample data, a value for r is obtained. This is called the test statistic. The absolute value of the test statistic is then compared to the appropriate value in a table of critical values of r.

Table of Critical Values for r

Conclusion n n If the absolute value of r exceeds the table value, we reject the null hypothesis which states that no significant linear correlation exists. If the absolute value of r does not exceed the table value, we fail to reject the null hypothesis.

Recall Linear Correlation n n n Association between 2 quantitative variables. Paired data (bivariate data). Scatter plot. Positive/Negative. Correlation coefficient, r. and …

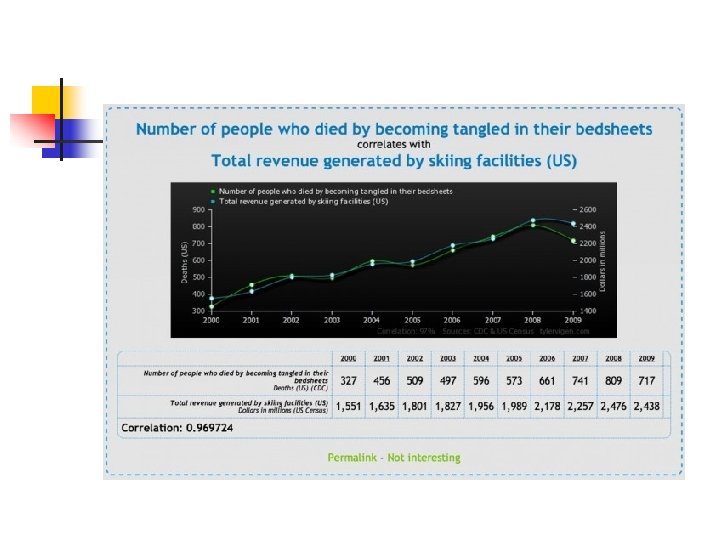
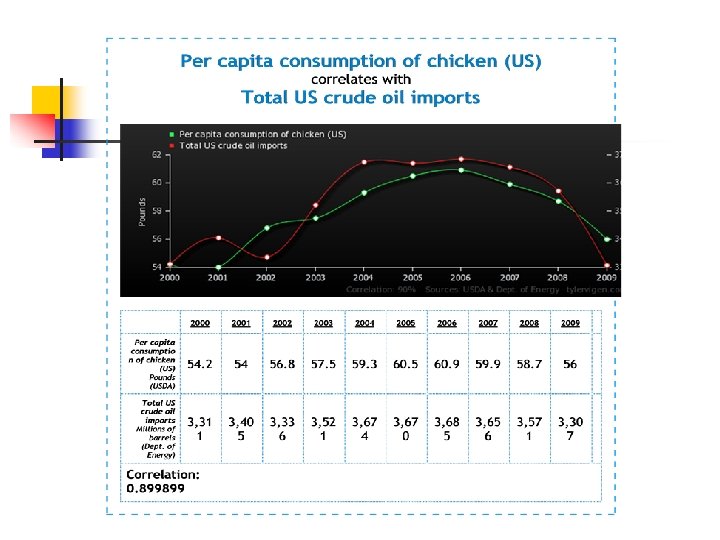
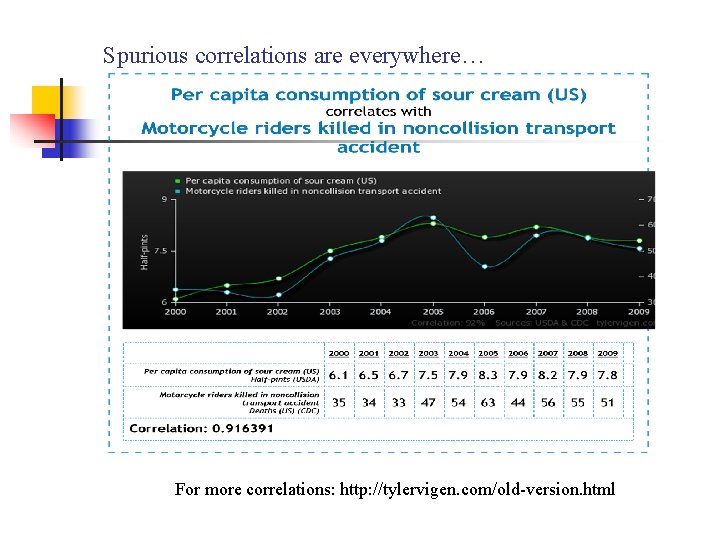
Spurious correlations are everywhere… For more correlations: http: //tylervigen. com/old-version. html