Correlation Coefficient and Line of Best Fit Correlation

Correlation Coefficient and Line of Best Fit

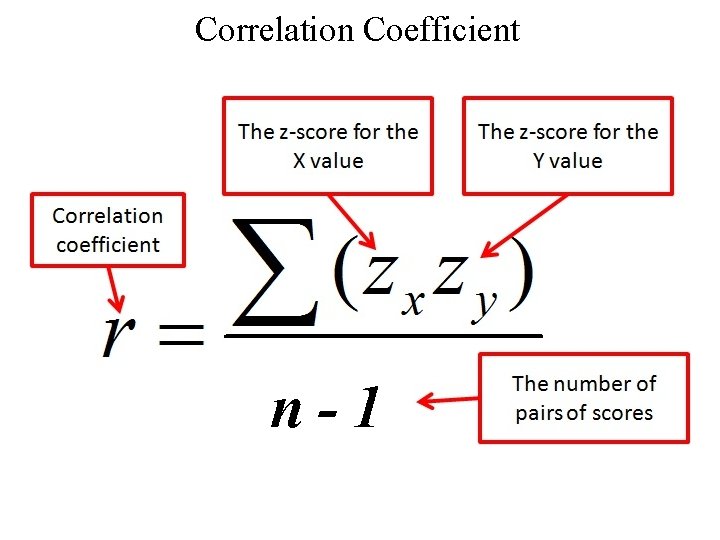
Correlation Coefficient r n-1

r • if the slope is + or • Strength: between -1 and 1 • Absolute value reflects strength Ex: -0. 7 and 0. 7 have the same strength. • Notation: rxy Ex: if looking at SAT and GPA write: r. SATGPA

r=1 r = -0. 54 r = 0. 85 Interpreting the Correlation Coefficient Size of r (absolute value) Relationship between the two variables 0. 8 -1 Very strong 0. 6 -0. 8 Strong 0. 4 -0. 6 Moderate 0. 2 -0. 4 Weak 0 -0. 2 No relationship

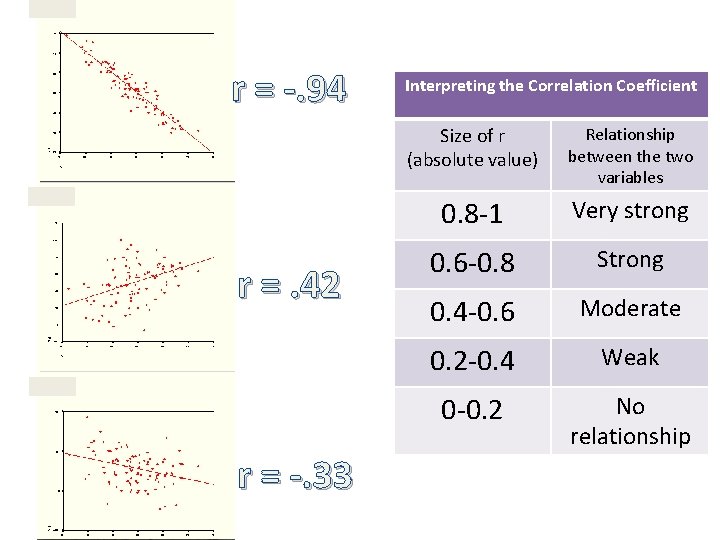
r = -. 94 r =. 42 r = -. 33 Interpreting the Correlation Coefficient Size of r (absolute value) Relationship between the two variables 0. 8 -1 Very strong 0. 6 -0. 8 Strong 0. 4 -0. 6 Moderate 0. 2 -0. 4 Weak 0 -0. 2 No relationship

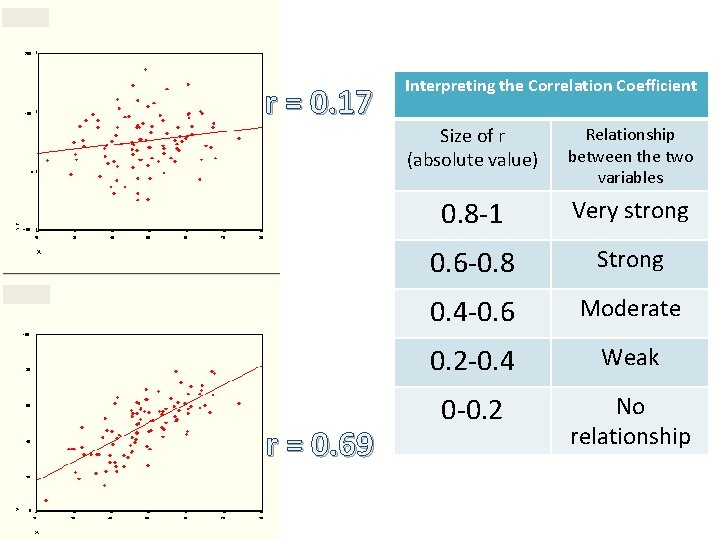
r = 0. 17 r = 0. 69 Interpreting the Correlation Coefficient Size of r (absolute value) Relationship between the two variables 0. 8 -1 Very strong 0. 6 -0. 8 Strong 0. 4 -0. 6 Moderate 0. 2 -0. 4 Weak 0 -0. 2 No relationship

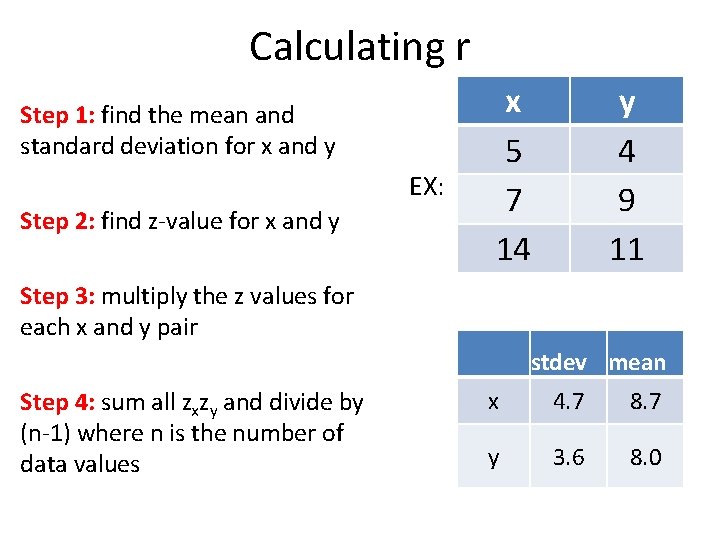
Calculating r Step 1: find the mean and standard deviation for x and y EX: Step 2: find z-value for x and y x 5 7 14 y 4 9 11 Step 3: multiply the z values for each x and y pair stdev mean Step 4: sum all zxzy and divide by (n-1) where n is the number of data values x 4. 7 8. 7 y 3. 6 8. 0

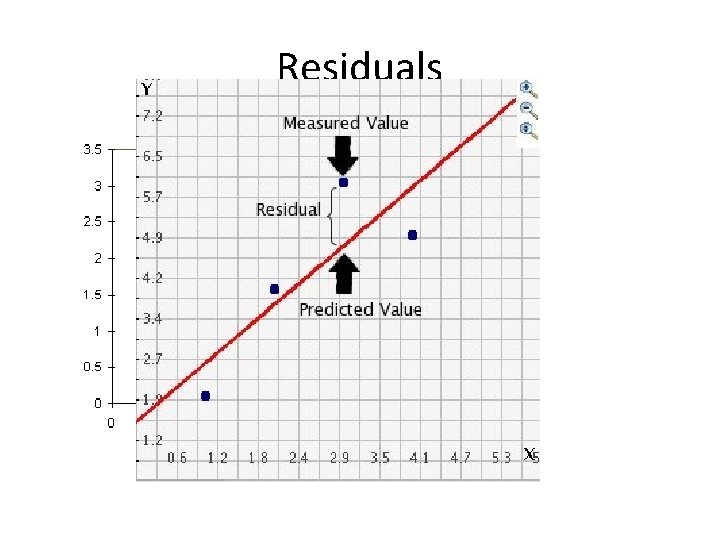
Residuals

• Can only use the line to make prediction when Best Fit Line conditions • Both variables are quantitative • The scatter plot is linear • No outlier is distorting results (you may have to take outliers out to check)

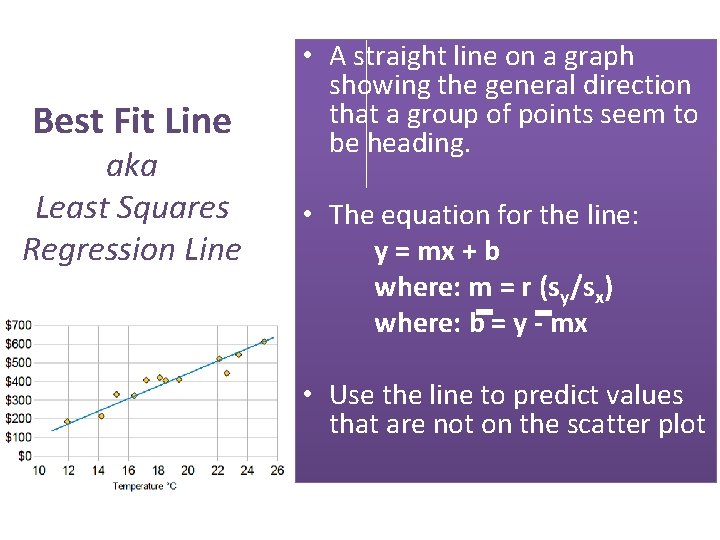
Best Fit Line aka Least Squares Regression Line • A straight line on a graph showing the general direction that a group of points seem to be heading. • The equation for the line: y = mx + b where: m = r (sy/sx) where: b = y - mx • Use the line to predict values that are not on the scatter plot

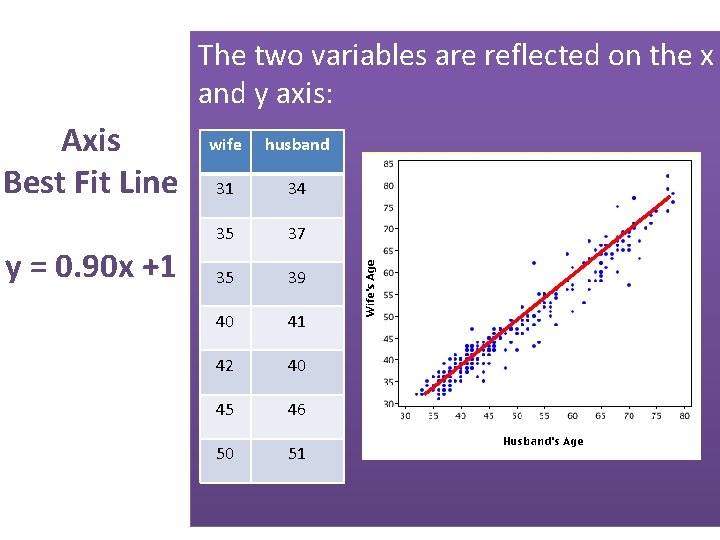
The two variables are reflected on the x and y axis: Axis Best Fit Line y = 0. 90 x +1 wife husband 31 34 35 37 35 39 40 41 42 40 45 46 50 51