Correlation and Regression Spearmans rank correlation An alternative

Correlation and Regression

Spearman's rank correlation • An alternative to correlation that does not make so many assumptions • Still measures the strength and direction of association between two variables • Uses the ranks instead of the raw data

Example: Spearman's rs VERSIONS: 1. Boy climbs up rope, climbs down again 2. Boy climbs up rope, seems to vanish, re-appears at top, climbs down again 3. Boy climbs up rope, seems to vanish at top 4. Boy climbs up rope, vanishes at top, reappears somewhere the audience was not looking 5. Boy climbs up rope, vanishes at top, reappears in a place which has been in full view

Hypotheses H 0: The difficulty of the described trick is not correlated with the time elapsed since it was observed. HA: The difficulty of the described trick is correlated with the time elapsed since it was observed.

East-Indian Rope Trick

East-Indian Rope Trick Years Impressiveness elapsed Score Rank Years Rank Impressiveness

East-Indian Rope Trick TABLE H n = 21, = 0. 05 Critical value: 0. 435 P < 0. 05, reject Ho

Spearman’s Rank Correlation - large n • For large n (> 100), you can use the normal correlation coefficient test for the ranks Under Ho, t has a t-distribution with n-2 d. f.

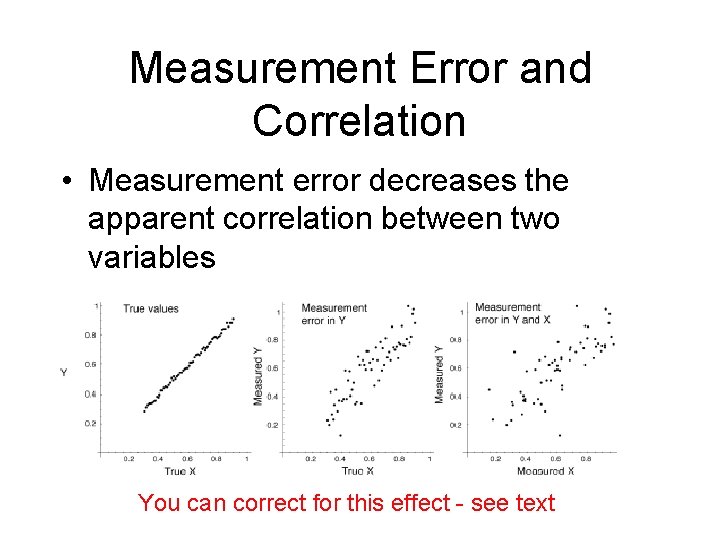
Measurement Error and Correlation • Measurement error decreases the apparent correlation between two variables You can correct for this effect - see text

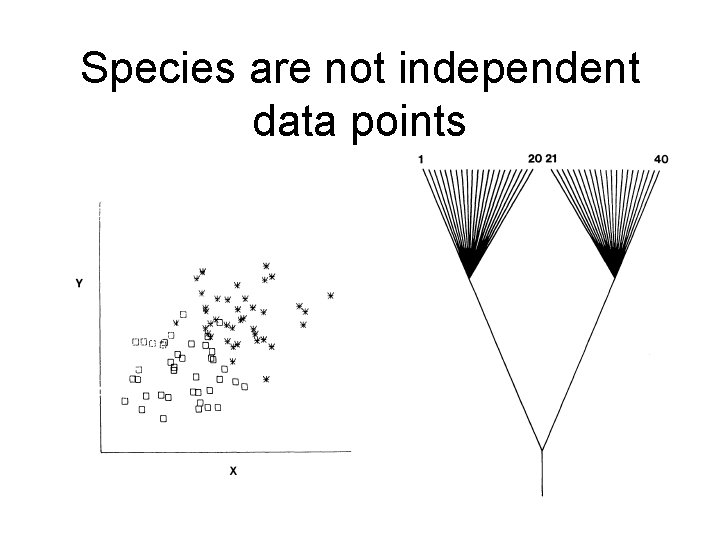
Species are not independent data points

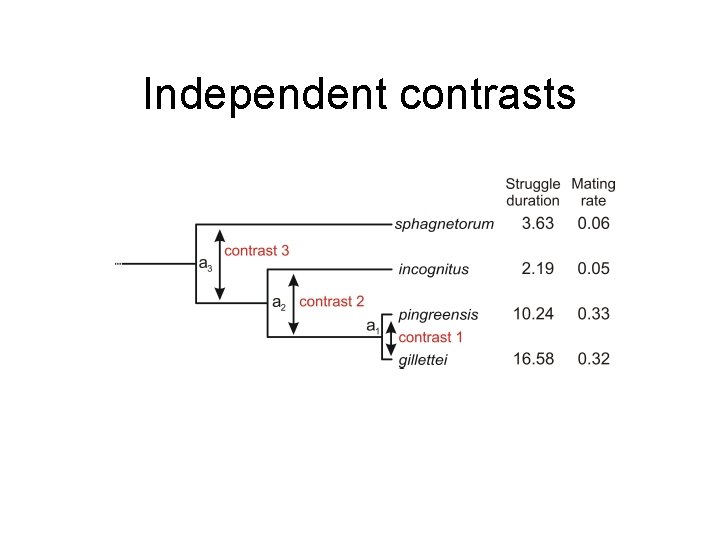
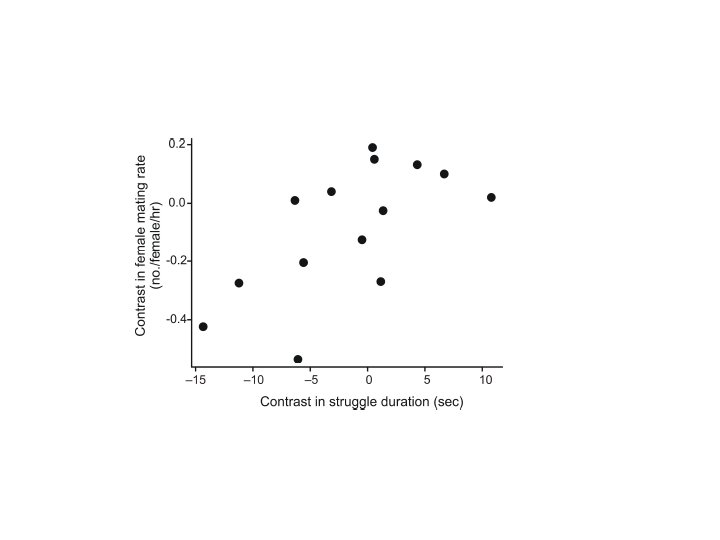
Independent contrasts

Independent contrasts

Quick Reference Guide Correlation Coefficient • What is it for? Measuring the strength of a linear association between two numerical variables • What does it assume? Bivariate normality and random sampling • Parameter: • Estimate: r • Formulae:

Quick Reference Guide - t-test for zero linear correlation • What is it for? To test the null hypothesis that the population parameter, , is zero • What does it assume? Bivariate normality and random sampling • Test statistic: t • Null distribution: t with n-2 degrees of freedom • Formulae:

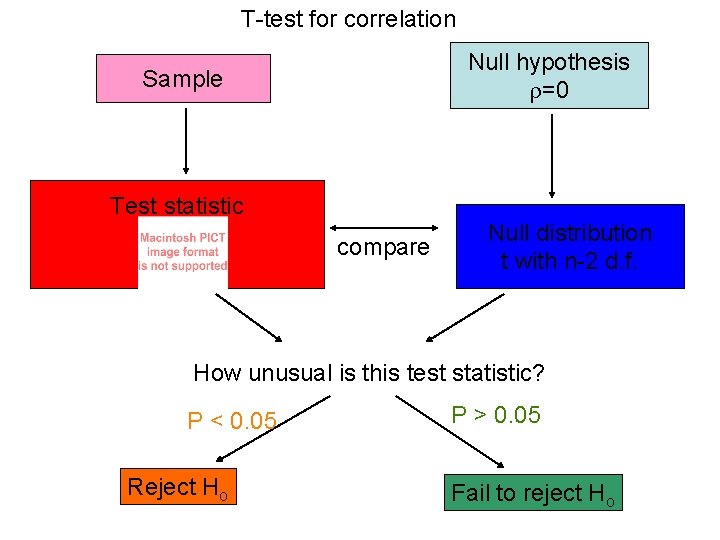
T-test for correlation Null hypothesis =0 Sample Test statistic compare Null distribution t with n-2 d. f. How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Quick Reference Guide Spearman’s Rank Correlation • What is it for? To test zero correlation between the ranks of two variables • What does it assume? Linear relationship between ranks and random sampling • Test statistic: rs • Null distribution: See table; if n>100, use t-distribution • Formulae: Same as linear correlation but based on ranks

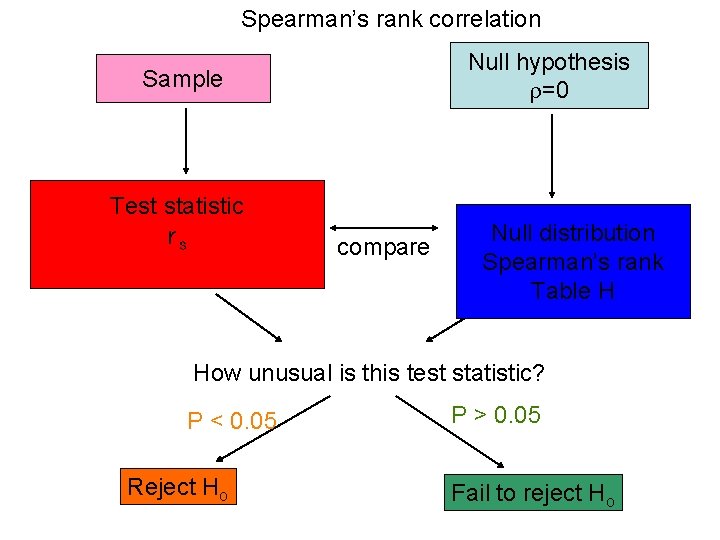
Spearman’s rank correlation Null hypothesis =0 Sample Test statistic rs compare Null distribution Spearman’s rank Table H How unusual is this test statistic? P < 0. 05 Reject Ho P > 0. 05 Fail to reject Ho

Quick Reference Guide Independent Contrasts • What is it for? To test for correlation between two variables when data points come from related species • What does it assume? Linear relationship between variables, correct phylogeny, difference between pairs of species in both X and Y has a normal distribution with zero mean and variance proportional to the time since divergence

Regression • The method to predict the value of one numerical variable from that of another • Predict the value of Y from the value of X • Example: predict the size of a dinosaur from the length of one tooth

Linear Regression • Draw a straight line through a scatter plot • Use the line to predict Y from X

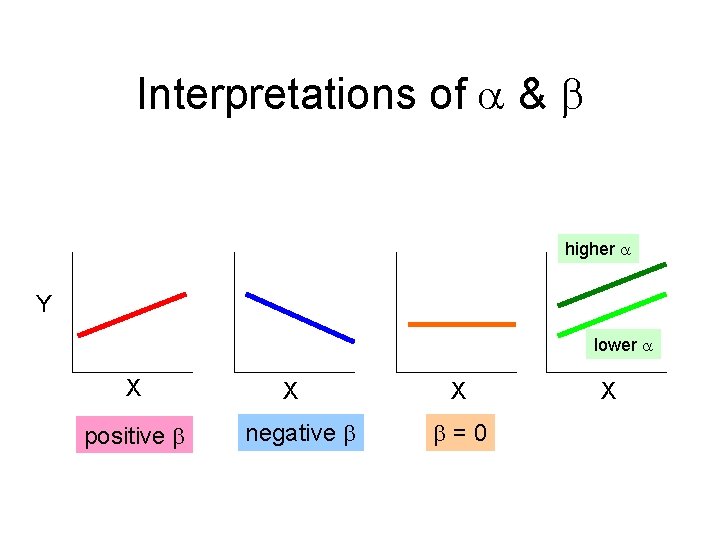
Linear Regression Formula Y = + X • = intercept – The predicted value of Y when X is zero • = slope – the rate of change in Y per unit of change in X Parameters

Interpretations of & higher Y lower X positive X negative X =0 X

Linear Regression Formula ^ Y = a + b. X • a = estimated intercept – The predicted value of Y when X is zero • b = estimated slope – the rate of change in Y per unit of change in X

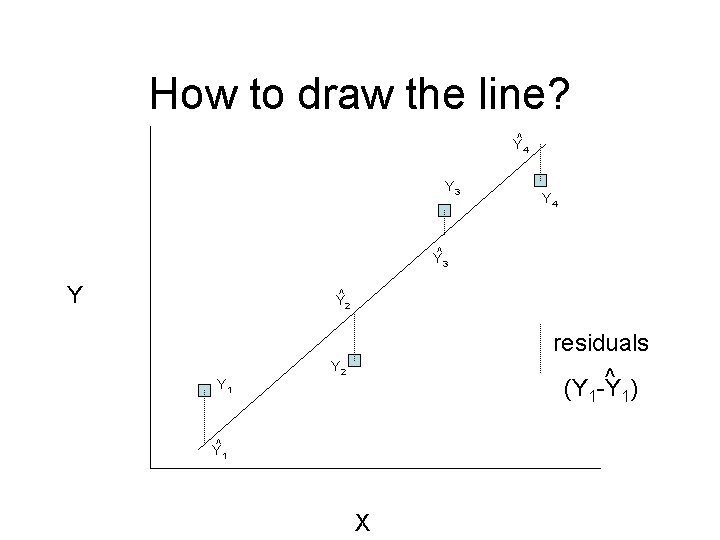
How to draw the line? Y^4 Y 3 Y 4 Y^3 Y Y^2 Y 1 residuals ^ ) (Y -Y Y 2 1 Y^1 X 1

Least-squares Regression • Draw the line that minimizes the sum of the squared residuals from the line ^ • Residual is (Yi-Yi) ^ 2 • Minimize the sum: SSresiduals=Σ(Yi-Yi)

Formulae for Least-Squares Regression • The slope and intercept that minimize the sum of squared residuals are: sum of products sum of squares for X

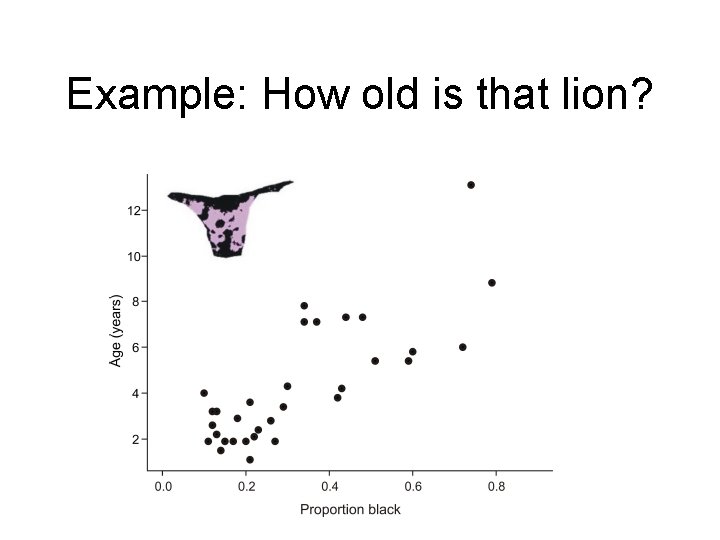
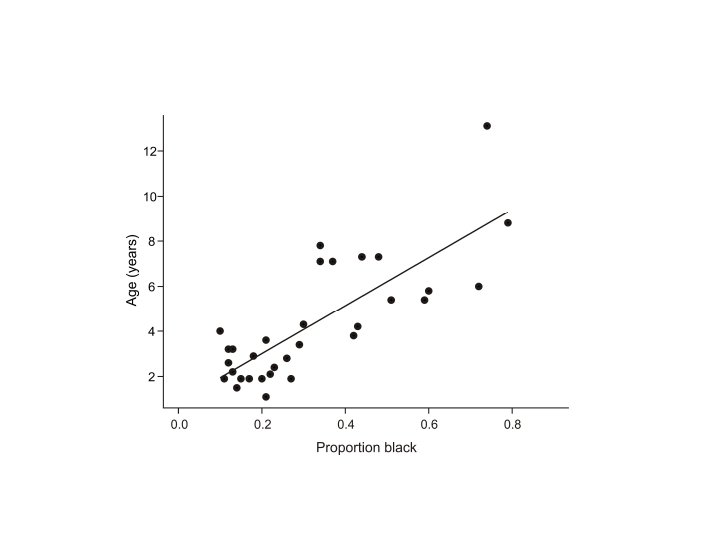
Example: How old is that lion? X = proportion black Y = age in years

Example: How old is that lion?

Example: How old is that lion? X = proportion black Y = age in years X = 0. 322 Y = 4. 309 Σ(X-X)2=1. 222 Σ(Y-Y)2=222. 087 Σ(X-X)(Y-Y)=13. 012

A certain lion has a nose with 0. 4 proportion of black. Estimate the age of that lion.

Standard error of the slope Sum of squares Sum of products

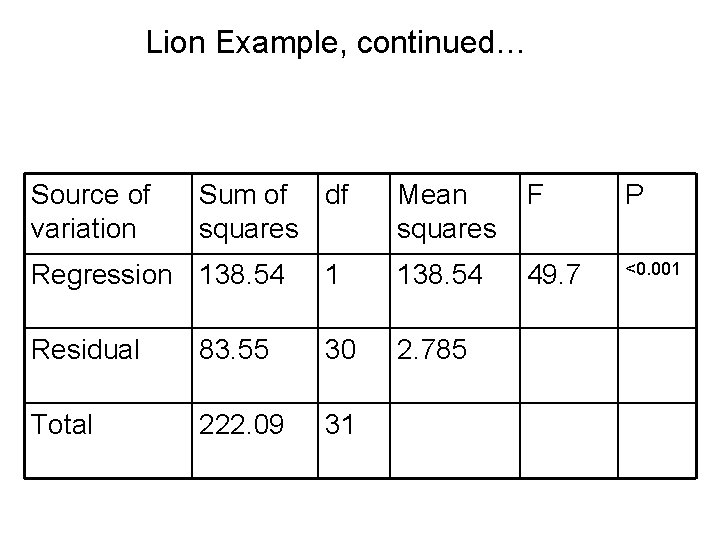
Lion Example, continued…

Confidence interval for the slope

Lion Example, continued…

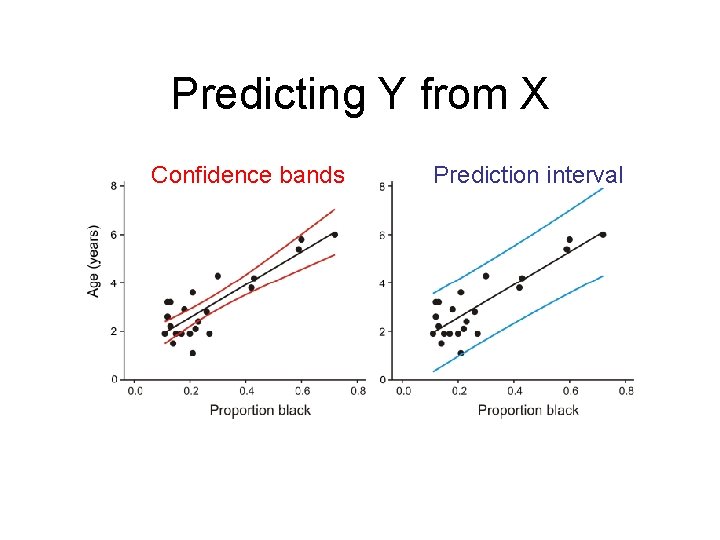
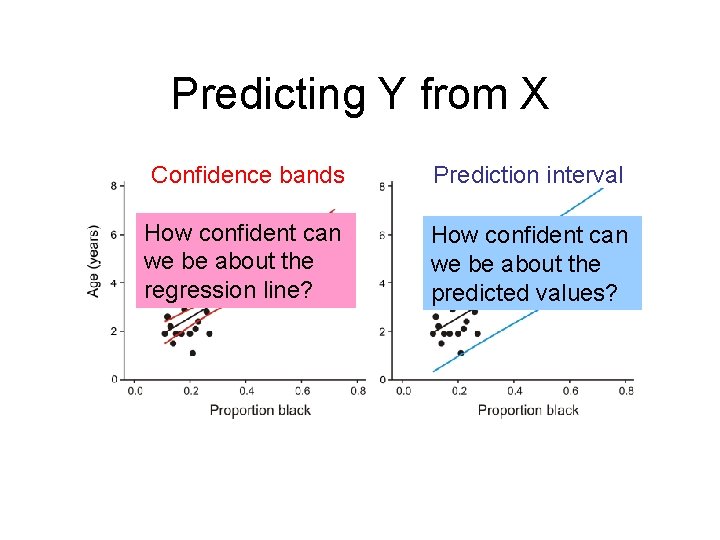
Predicting Y from X • What is our confidence for predicting Y from X? • Two types of predictions: • What is the mean Y for each value of X? – Confidence bands • What is a particular individual Y at each value of X? – Prediction intervals

Predicting Y from X • Confidence bands: measure the precision of the predicted mean Y for each value of X • Prediction intervals: measure the precision of predicted single Y values for each value of X

Predicting Y from X Confidence bands Prediction interval

Predicting Y from X Confidence bands Prediction interval How confident can we be about the regression line? How confident can we be about the predicted values?

Testing Hypotheses about a Slope • t-test for regression slope • Ho: There is no linear relationship between X and Y ( = 0) • Ha: There is a linear relationship between X and Y ( ≠ 0)

Testing Hypotheses about a Slope • Test statistic: t • Null distribution: t with n-2 d. f.

Lion Example, continued… df = n-2 = 32 -2 = 30 Critical value: 2. 04 7. 05 > 2. 04 so we reject the null hypothesis Conclude that 0

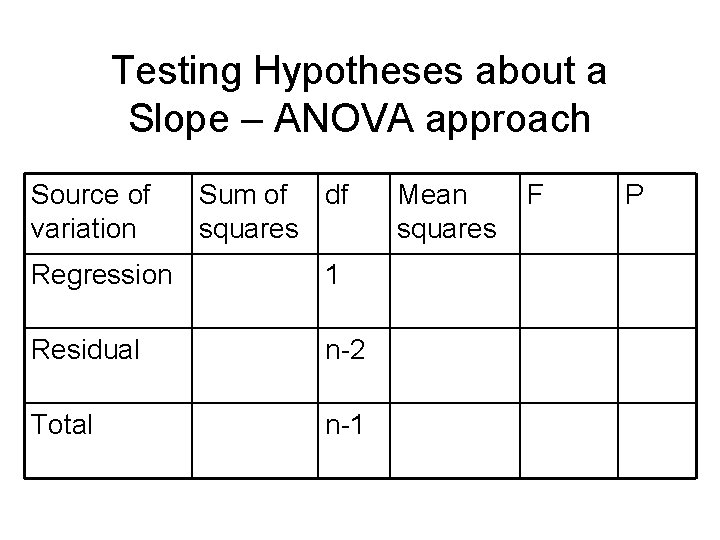
Testing Hypotheses about a Slope – ANOVA approach Source of variation Sum of df squares Regression 1 Residual n-2 Total n-1 Mean squares F P

Lion Example, continued… Source of variation Sum of df squares Mean squares F P 49. 7 <0. 001 Regression 138. 54 1 138. 54 Residual 83. 55 30 2. 785 Total 222. 09 31

Testing Hypotheses about a Slope – R 2 • R 2 measures the fit of a regresion line to the data R 2 = SSregression SStotal • Gives the proportion of variation in Y that is explained by variation in X

Lion Example, Continued

Assumptions of Regression • At each value of X, there is a population of Y values whose mean lies on the “true” regression line • At each value of X, the distribution of Y values is normal • The variance of Y values is the same at all values of X • At each value of X the Y measurements represent a random sample from the population of Y values

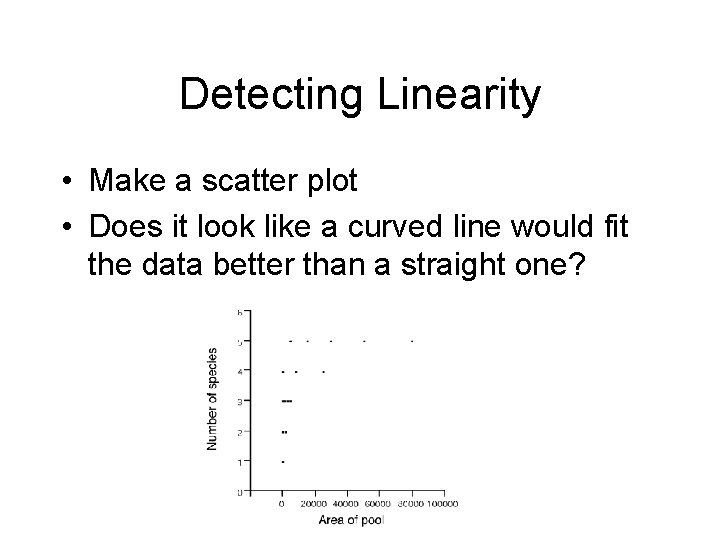
Detecting Linearity • Make a scatter plot • Does it look like a curved line would fit the data better than a straight one?

Non-linear relationship: Number of fish species vs. Size of desert pool

Taking the log of area:

Detecting non-normality and unequal variance • These are best detected with a residual plot ^ • Plot the residuals (Yi-Yi) against X • Look for: – symmetric cloud of points – Little noticeable curvature – Equal variance above and below the line

Residual plots help assess assumptions Original: Residual plot

Transformed data Logs: Residual plot

What if the relationship is not a straight line? • Transformations • Non-linear regression

Transformations • Some (but not all) nonlinear relationships can be made linear with a suitable transformation • Most common – log transform Y, X, or both