Correlation and Regression Introduction to linear correlation and

Correlation and Regression • • • Introduction to linear correlation and regression Numerical illustrations R and linear correlation/regression Assumptions of linear correlation/regression Model II regression Xuhua Xia

Introduction • Correlation – – Bivariate correlation Multiple correlation Partial correlation Canonical correlation • Regression (1857 -1936) – Simple regression – Multiple regression – Nonlinear regression Xuhua Xia (1822 -1911) (1890 -1962)

Regression Coefficient Sum X Y 1 1 4 4 4 2 2 1 1 1 3 3 0 0 0 4 4 1 1 1 5 5 4 4 4 15 15 10 10 10 Assignment: Change Y to 3, 4, 5, 6, 7 and re-compute a, b and r. X, Y. Print the slide and hand it in. Xuhua Xia

Correlation & Regression Coefficients Sum Xuhua Xia X Y 1 5 4 4 -4 2 4 1 1 -1 3 3 0 0 0 4 2 1 1 -1 5 1 4 4 -4 15 15 10 10 -10

Regression Coefficient Sum Xuhua Xia X Y 1 1 4 4 4 2 1 1 4 2 3 3 0 0 0 4 5 1 4 2 5 5 4 4 4 15 15 10 16 12

Least-squares method Least-square estimate of the sample mean Xuhua Xia

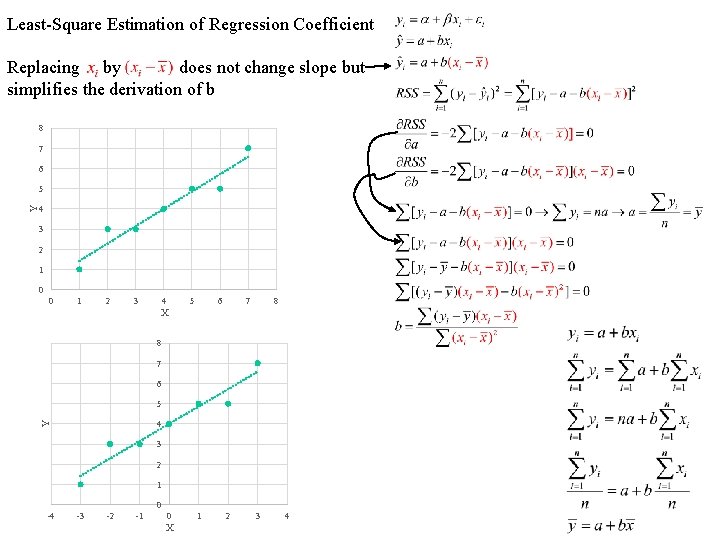
Least-Square Estimation of Regression Coefficient Replacing by does not change slope but simplifies the derivation of b 8 7 6 4 3 2 1 0 0 1 2 3 4 5 6 7 8 X 8 7 6 5 4 Y Y 5 3 2 1 0 -4 -3 -2 -1 0 X 1 2 3 4

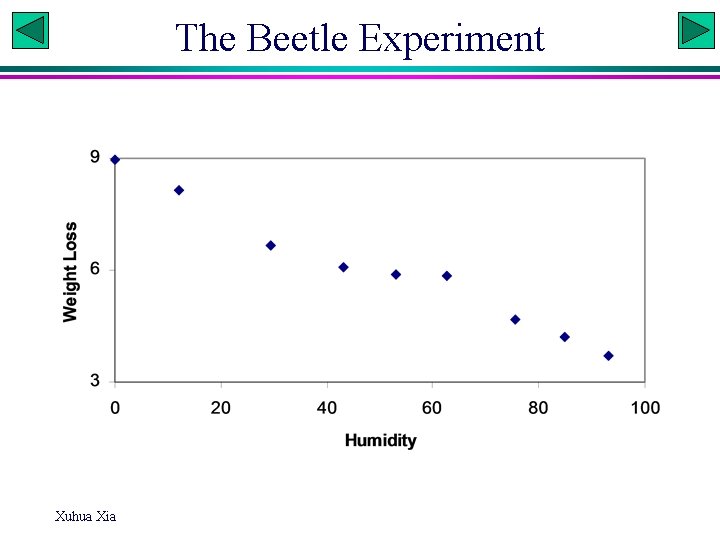
The Beetle Experiment Xuhua Xia

Regression Coefficient Assignment: Add 1 to X and insert your own estimates (from the new data set) into the equations in red. Print and hand in the slide. 95% CI: b t 0. 05, df*sb Xuhua Xia Calculation of SE for a will be illustrated later

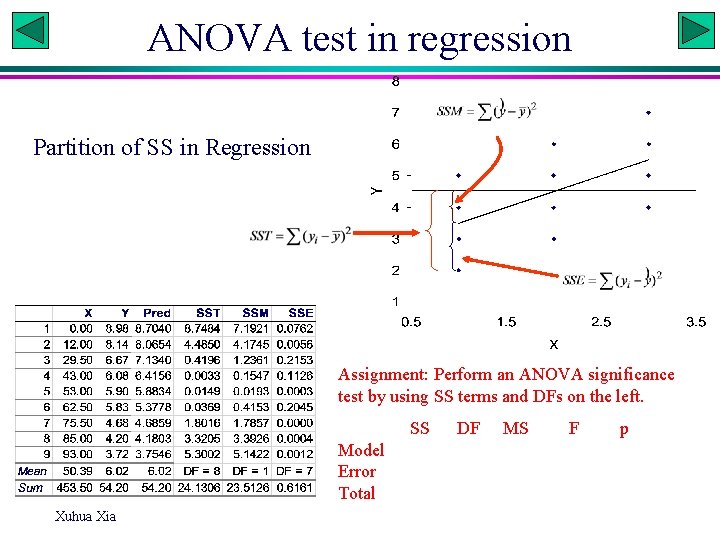
ANOVA test in regression Partition of SS in Regression Assignment: Perform an ANOVA significance test by using SS terms and DFs on the left. SS Model Error Total Xuhua Xia DF MS F p

Regression functions in R fit<-lm(y~x 1+x 2+x 3+ …); wfit<-lm(y~x 1, weights=w) ypred t 0. 05, df*SEy, default level is fit<-lm(y~x+0) 95%, i. e. , adding 'level=0. 95' fit<-lm(y~x 1*x 2) will have the same output fit<-lm(y~(x 1+x 2+x 3…)^2 summary(fit) anova(fit) Output SEy for ypred at x coef(fit) = 4 confint(fit) deviance(fit)= RSS res<-resid(fit) 95% CL of "future" y pred<-fitted(fit) OR pred<-predict(fit) at a particular x new. D<-data. frame(x=4); predict(fit, new. D, se. fit=TRUE) predict(fit, new. D, interval="confidence") predict(fit, new. D, interval="prediction") new. D<-data. frame(x=seq(-3, 3, 0. 5)) predict(fit, new. D, se. fit=T) pred. w. clim<-predict(fit, new. D, interval="confidence") pred. w. plim<-predict(fit, new. D, interval="prediction")

R graphics with regression fit<-lm(Wt. Loss~Humid, data=md) plot(Humid, resid(fit)) plot(density(resid(fit))) plot(Humid, Wt. Loss) abline(fit, col="red") # plot confidence intervals of predicted values. new<-data. frame(Humid=seq(0, 100, 5)) plim <- predict(fit, new, interval = "prediction") clim <- predict(fit, new, interval = "confidence") matplot(new$Humid, cbind(clim, plim[, -1]), lty = c(1, 2, 2, 3, 3), type = "l", ylab = "predicted y") When you have a data set (dat. Set) with, say 5, columns and you wish to omit the 3 rd column, issue dat. Set[, -3] Confidence Prediction Xuhua Xia

summary(fit) & anova(fit) Residuals: Min 1 Q -0. 46397 -0. 03437 Median 0. 01675 3 Q 0. 07464 Max 0. 45236 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 8. 704027 0. 191565 45. 44 6. 54 e-10 *** x -0. 053222 0. 003256 -16. 35 7. 82 e-07 *** Residual standard error: 0. 2967 on 7 degrees of freedom Multiple R-squared: 0. 9745, Adjusted R-squared: 0. 9708 F-statistic: 267. 2 on 1 and 7 DF, p-value: 7. 816 e-07 Response: y Df Sum Sq Mean Sq F value Pr(>F) x 1 23. 5145 23. 515 267. 18 7. 816 e-07 Residuals 7 0. 6161 0. 088 n = 9: Num. of cases m=1: Num. of IV

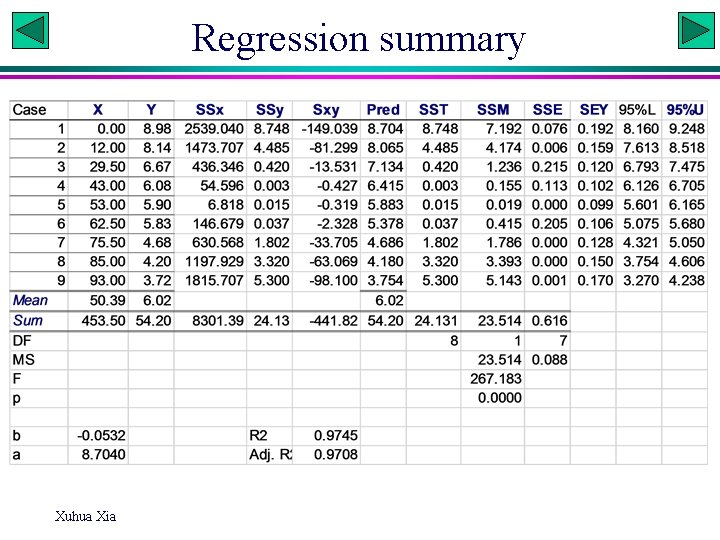
Regression summary Xuhua Xia

Assumptions • The regression model Yi = + Xi + i • Assumptions – The error term has a mean = 0, is independent and normally distributed at each value of X, and have the same variance at each value of X (homoscedasticity). – Y is linearly related to X – There is negligible error (e. g. , measurement error) for X. (Model II regression) • Conceptual problem: sensitive to outliers • Least-deviation, i. e. , minimize abs(EY -Y) Xuhua Xia

Model II regression r<-prcomp(~Humid+Wt. Loss) slope<-r$rotation[2, 1]/r$rotation[1, 1] b <-r$rotation[2, 1]/r$rotation[1, 1] a<-r$center[2] - b*r$center[1] a; b Wt. Loss 8. 704226 -0. 05322609 get. Reg. B<-function(md, indices, b) { r<-prcomp(~Humid+Wt. Loss, data=md, subset=indices) b[2]<-r$rotation[2, 1]/r$rotation[1, 1] b[1]<-r$center[2]-b[2]*r$center[1] return(b) } library(boot) b<-c(0, 0) boot. data<-data. frame(Humid=Humid, Wt. Loss=Wt. Loss) reps<-boot(boot. data, get. Reg. B, R=1000, b=b) print(reps, digits=5) Bootstrap Statistics : original bias t 1* 8. 704226 -0. 04528448 Xuhua Xia t 2* -0. 053226 0. 00065625 std. error 0. 2261472 0. 0034164

Least-absolute-deviation method Use the beetle data: X<-md$Humid > sol Y<-md$Wt. Loss $par my. Fun<-function(x) { [1] 8. 79385823 -0. 05448819 EY<- x[1]+x[2]*X abs. Diff<-abs(Y-EY) $value sum. D<-sum(abs. Diff) [1] 1. 565197 } sol<-optim(c(9, -0. 05), my. Fun) my. Fun 2<-function(x, md) { X<-md$Humid Y<-md$Wt. Loss EY<- x[1]+x[2]*X abs. Diff<-abs(Y-EY) sum. D<-sum(abs. Diff) print(reps, digits=4) } Bootstrap Statistics : get. Reg. B<-function(md, indices, b) { original bias std. error nd<-md[indices, ] t 1* 8. 79386 -0. 092608 0. 345932 sol<-optim(b, my. Fun 2, md=nd) t 2* -0. 05449 0. 001274 0. 004784 b<-sol$par return(b) } library(boot) boot. data<-data. frame(Humid=Humid, Wt. Loss=Wt. Loss) b<-c(9, -0. 05) reps<-boot(boot. data, get. Reg. B, R=1000, b=b) Slide 18

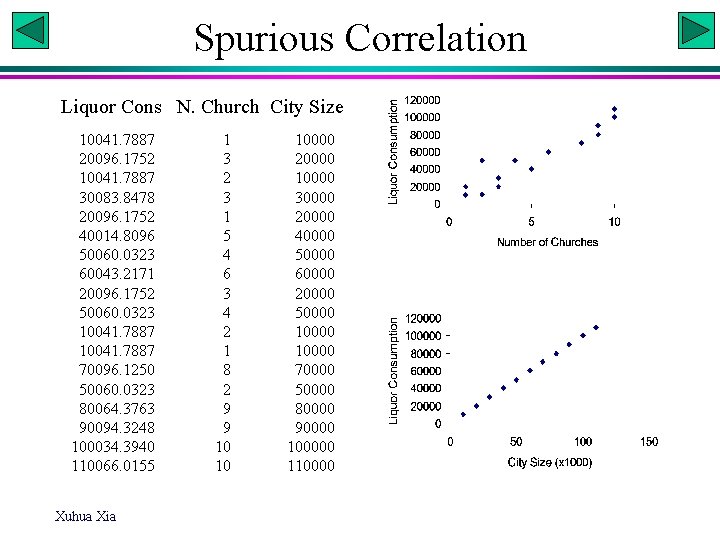
Spurious Correlation Liquor Cons N. Church City Size 10041. 7887 20096. 1752 10041. 7887 30083. 8478 20096. 1752 40014. 8096 50060. 0323 60043. 2171 20096. 1752 50060. 0323 10041. 7887 70096. 1250 50060. 0323 80064. 3763 90094. 3248 100034. 3940 110066. 0155 Xuhua Xia 1 3 2 3 1 5 4 6 3 4 2 1 8 2 9 9 10 10 10000 20000 10000 30000 20000 40000 50000 60000 20000 50000 10000 70000 50000 80000 90000 100000 110000