Correlation and Prediction ice cream cone sales and

Correlation and Prediction: ice cream cone sales and shark bites …. what is their relationship? Professor Patricia Eckardt Adelphi University 2007

CSI for ice cream cones and shark bites. . • Every summer in the vacation town of Sunny beach USA the sales of ice cream cones increase as does the incidence of shark bites? • What sinister plot is occurring here? Are people coming to Sunny beach USA to buy ice cream and then leisurely watch the shark attacks? • Are sharks angry at the people for not sharing the ice cream and so they attack them? • Do sharks like the taste of people who eat a lot of ice cream better than those who eat little to no ice cream before a swim? Professor Patricia Eckardt Adelphi University 2007

There appears to be a Correlation between the two variables of ice cream sales and shark bites. . • Correlation is a statistic for describing the relationship between two variables – Examples • • Maternal cigarette smoking and fetal birth weight Hours of studying and grades on a statistics exam Years of Hypertension and risk of a CVA Exposure to sun and incidence of melanoma. Professor Patricia Eckardt Adelphi University 2007

Like all data analysis, drawing a picture helps to get an idea of what is going on between your 2 variables. One way to represent a correlation between 2 variables is to graph it on a Scatter Diagram. The scattergram on the next slide contains fabricated data to illustrate the correlation between maternal cigarette consumption and fetal birth wt. Professor Patricia Eckardt Adelphi University 2007

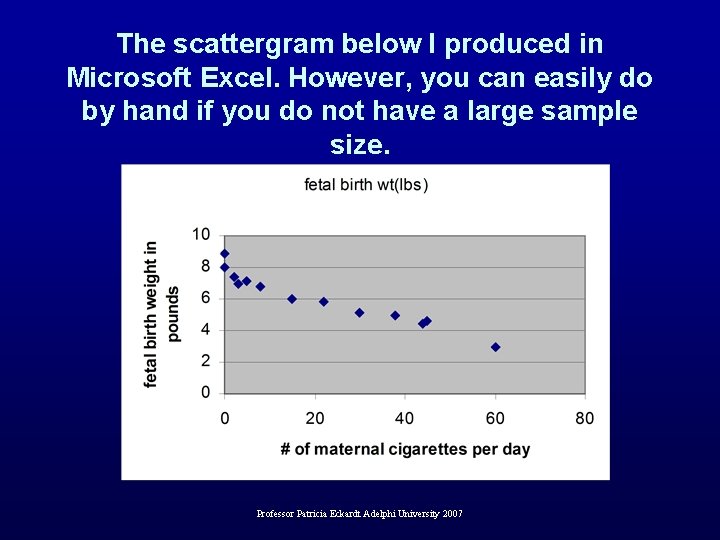
The scattergram below I produced in Microsoft Excel. However, you can easily do by hand if you do not have a large sample size. Professor Patricia Eckardt Adelphi University 2007

Graphing Correlations on a Scatter Diagram • Steps for making a scatter diagram 1. The predictor variable goes on the x axis, and the dependent variable goes on the y axis. 2. Draw axes and assign variables to them (years of hypertension (X axis) and incidence of CVA (y axis)). 2. Determine the range of values for each variable and mark the axes 3. Mark a dot for each subjects pair of scores. For example go to scattergram on slide 5, and move finger along x axis just past the # 20, then run finger up until you come to point. The y axis value for this point is roughly 6. The value for this subject is: ( 22, 6). The x value always comes first, then the y and this point represents the data subject where: mom smokes 22 cigs a day, fetal bw 5. 8 lbs. Professor Patricia Eckardt Adelphi University 2007

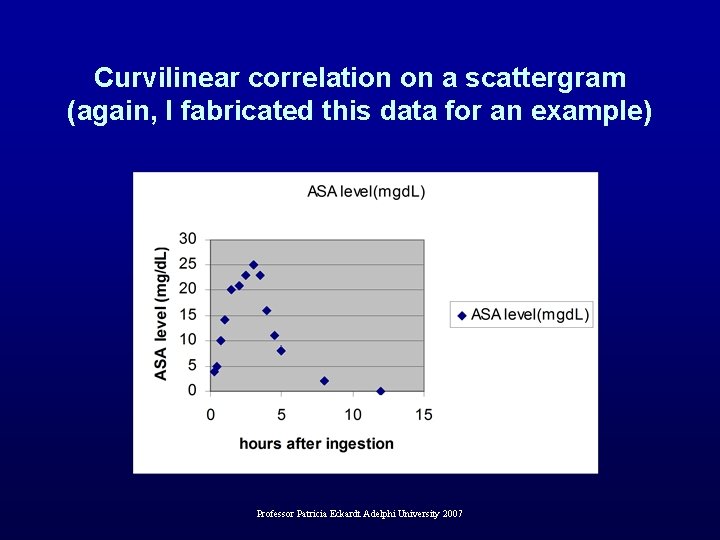
Correlation: variables can have a linear or curvilinear relationship • Linear correlation – Pattern on a scatter diagram is a straight line: like the maternal cigarettes and fetal birth weight example. • Curvilinear correlation – More complex relationship between variables – Pattern in a scatter diagram is not a straight line: this could be a drug blood level over an 8 hour period ( slow rise , peaks, and drops off). Example on next slide. Professor Patricia Eckardt Adelphi University 2007

Curvilinear correlation on a scattergram (again, I fabricated this data for an example) Professor Patricia Eckardt Adelphi University 2007

Takeaway slide • The reason why it is SO important to graph correlation data is that with correlation data (where you may later try and make predictions with regression), if the data is not linear, you cannot use the standard regression equation as the underlying assumption is one of linear relationship of variables. Unfortunately: many researchers not trained in statistic theory just apply the statistical software without first LOOKING at their data. ALWAYS DRAW A PICTURE of your data. • If your data is not linear, do not panic : just identify it and there are transformations of data OR modification of formula to account for quadratic, that will still allow you to assess relationship. These techniques are not covered in this course, but I would be happy to discuss off line if you are interested. Professor Patricia Eckardt Adelphi University 2007

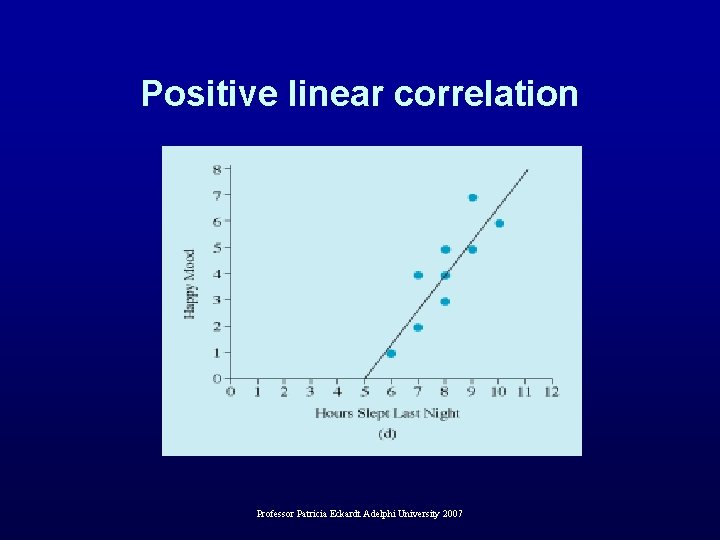
Positive linear correlation – High scores on one variable matched by high scores on another – Line slants up to the right Professor Patricia Eckardt Adelphi University 2007

Positive linear correlation Professor Patricia Eckardt Adelphi University 2007

Negative linear correlation – High scores on one variable matched by low scores on another – Line slants down to the right Professor Patricia Eckardt Adelphi University 2007

Negative linear correlation Professor Patricia Eckardt Adelphi University 2007

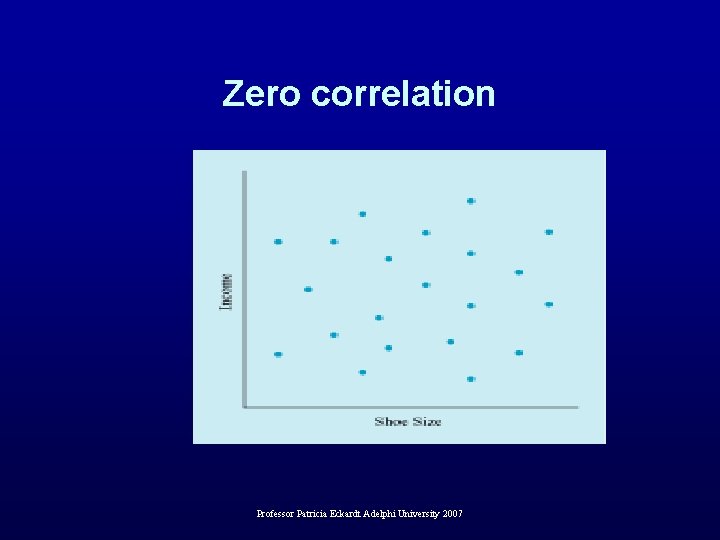
Zero correlation – No line, straight or otherwise, can be fit to the relationship between the two variables – Two variables are said to be “uncorrelated” – Looks like a “buck shot blast” Professor Patricia Eckardt Adelphi University 2007

Zero correlation Professor Patricia Eckardt Adelphi University 2007

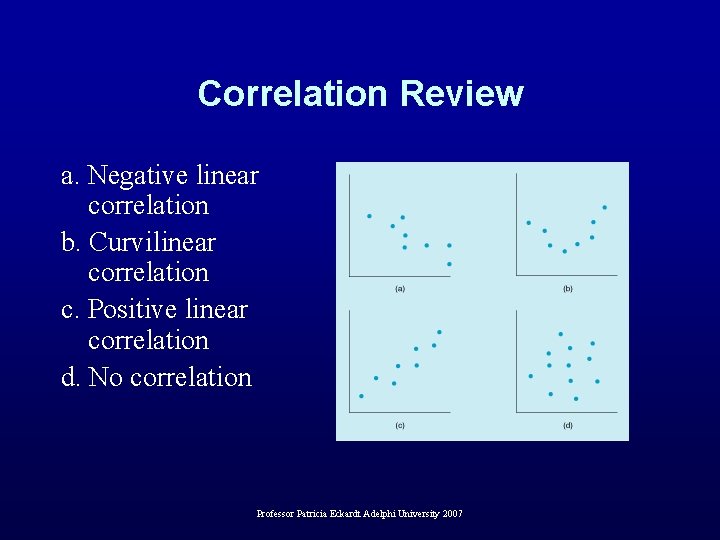
Correlation Review a. Negative linear correlation b. Curvilinear correlation c. Positive linear correlation d. No correlation Professor Patricia Eckardt Adelphi University 2007

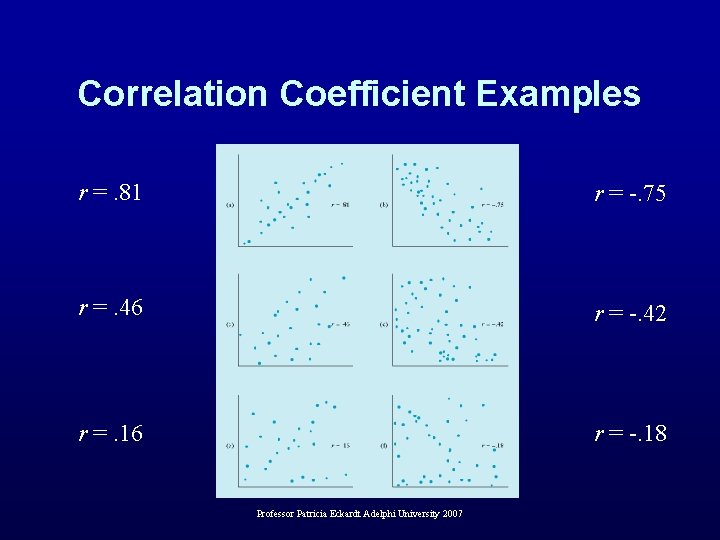
Correlation Coefficient • Correlation coefficient, r, indicates the precise degree of linear correlation between two variables • Computed by taking “cross-products” of Z scores – Multiply Z score on one variable by Z score on the other variable – Compute average of the resulting products • Can vary from – -1 (perfect negative correlation) – through 0 (no correlation) – to +1 (perfect positive correlation) Professor Patricia Eckardt Adelphi University 2007

Correlation Coefficient Examples r =. 81 r = -. 75 r =. 46 r = -. 42 r =. 16 r = -. 18 Professor Patricia Eckardt Adelphi University 2007

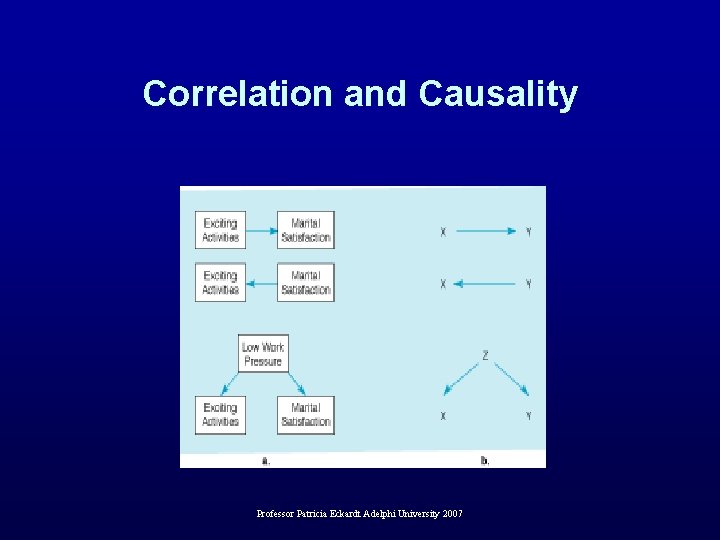
Correlation and Causality • When two variables are correlated, three possible directions of causality – 1 st variable causes 2 nd – 2 nd variable causes 1 st – Some 3 rd variable causes both the 1 st and the 2 nd • Inherent ambiguity in correlations • See next slide for pictorial representation of these concepts. . Professor Patricia Eckardt Adelphi University 2007

Correlation and Causality Professor Patricia Eckardt Adelphi University 2007

TAKEAWAY: Correlation and Causality • Knowing that two variables are correlated tells you nothing about their causal relationship • More information about causal relationships can be obtained from – A longitudinal study—measure variables at two or more points in time – A true experiment—randomly assign participants to a particular level of a variable Professor Patricia Eckardt Adelphi University 2007

Statistical Significance of a Correlation • Correlations are sometimes described as being “statistically significant” – There is only a small probability that you could have found the correlation you did in your sample if in fact the overall group had no correlation – If probability is less than 5%, one says “p <. 05” Professor Patricia Eckardt Adelphi University 2007

Prediction • Correlations can be used to make predictions about scores – Predictor • X variable • Variable being predicted from – Criterion • Y variable • Variable being predicted • Sometimes called “regression” Professor Patricia Eckardt Adelphi University 2007

Prediction • Predicted Z score on the criterion variable can be found by multiplying Z score on the predictor variable by that standardized regression coefficient – Standardized regression coefficient is the same thing as the correlation – For raw score predictions • Change raw score to Z score • Make prediction • Change back to raw score Professor Patricia Eckardt Adelphi University 2007

Multiple Correlation and Multiple Regression • Multiple correlation – Association between criterion variables and two or more predictor variables • Multiple regression – Making predictions about criterion variables based on two or more predictor variables – Unlike prediction from one variable, standardized regression coefficient is not the same as the ordinary correlation coefficient Professor Patricia Eckardt Adelphi University 2007

Proportion of Variance Accounted For; • Correlation coefficients – Indicate strength of a linear relationships – Cannot be compared directly • To compare correlation coefficients, square them – An r of. 40 yields an r 2 of. 16; an r of. 20 an r 2 of. 04 – Squared correlation indicates the proportion of variance on the criterion variable accounted for by the predictor variable. So, if I have an r 2 of. 16 then I have accounted for 16% of the variance in y by using x to predict it. Professor Patricia Eckardt Adelphi University 2007

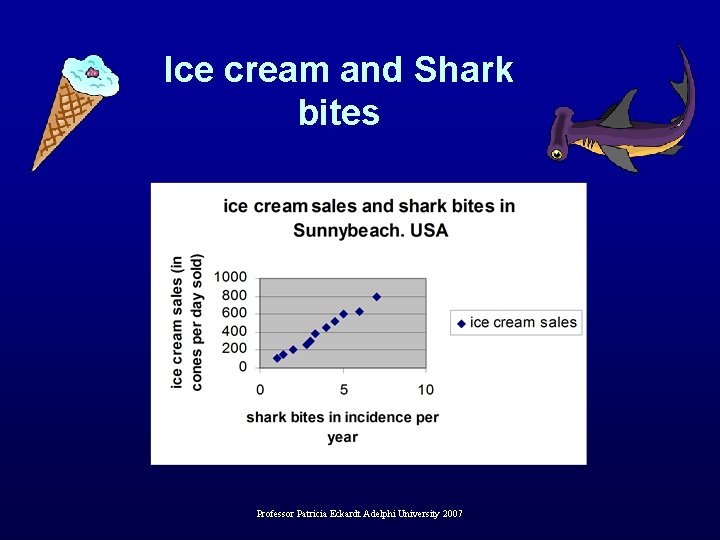
Now lets take what we have learned and solve the ice cream sales and shark bite mystery in Sunnybeach USA • The data looks as if that every summer as shark bites increase, so does the sale of ice cream cones in this resort town. • So, lets draw a picture of the data. Professor Patricia Eckardt Adelphi University 2007

Ice cream and Shark bites Professor Patricia Eckardt Adelphi University 2007

Ice cream and Shark bites • Well it appears to be a definite correlation. • A positive one at that: as one variable increase, so does the other one…… Professor Patricia Eckardt Adelphi University 2007

Ice cream and Shark bites • So, which is it? DO the ice cream fed swimmers bring the sharks? • Or do the shark attacks bring spectators who crave ice cream? • OR, like MUCH research is there a third unidentified variable that may account for the increase in both……? Professor Patricia Eckardt Adelphi University 2007

Keep thinking of possible confounding or spurious unidentified variables • Perhaps an increase in the temperature in the summer months, brings an increase in the number of people to the beach. The people eat more ice cream and swim to cool off…. The sharks have always been in the water, except now that there are more people in the water , there is an increased chance of shark bites occurring. • Our original hypotheses of shark bites and ice cream cones having some type of direct causal relationship is probably untrue. Professor Patricia Eckardt Adelphi University 2007

TAKEAWAY • Correlation between variables does NOT prove causation. I for one, was very skeptical of our 3 original hypotheses regarding ice cream and shark bites in slide 2… • Frequently there are other unidentified variables (latent) that may be involved in any proposed research relationship. • When you read research, remember that, and be a thinking reader, what variable could they be missing in their hypothesis? • More importantly: when you conduct research, apply this exhaustive search for latent variables that may be affecting the variables you are measuring! Professor Patricia Eckardt Adelphi University 2007