Correlation and Linear Regression Chapters 6 and 7

Correlation and Linear Regression Chapters 6 and 7

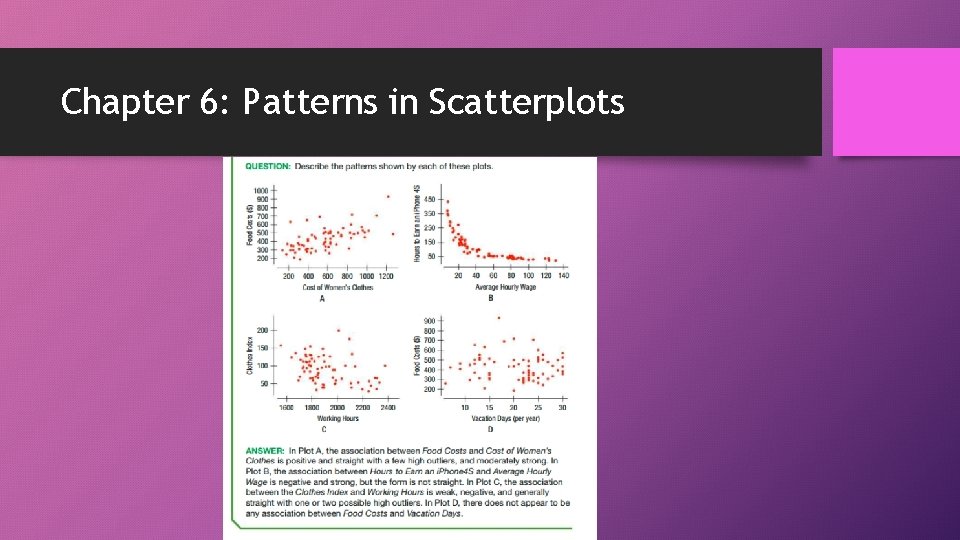
Chapter 6: Patterns in Scatterplots

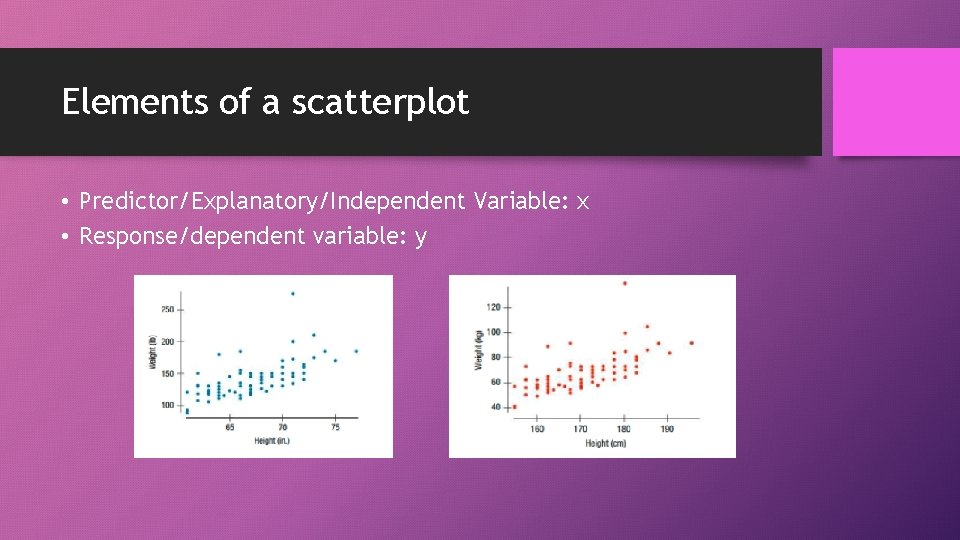
Elements of a scatterplot • Predictor/Explanatory/Independent Variable: x • Response/dependent variable: y

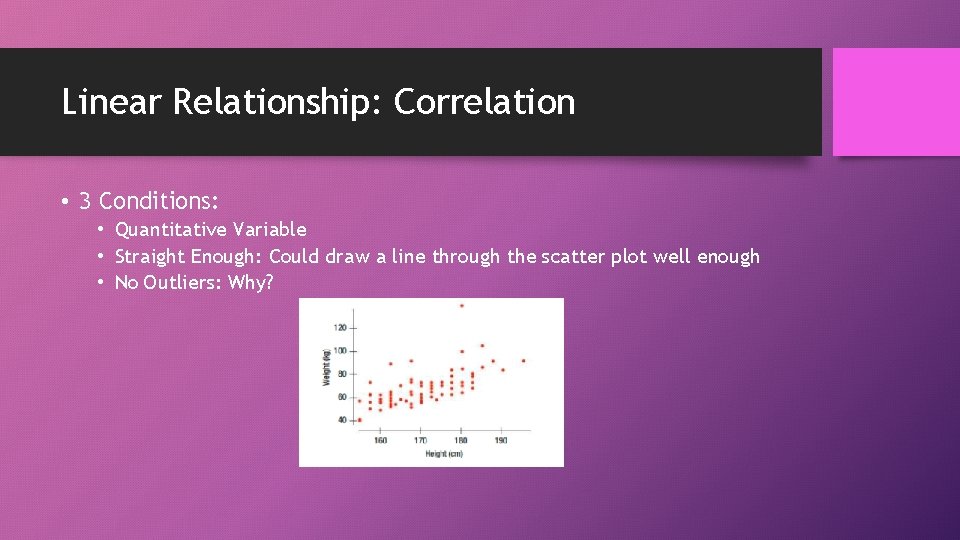
Linear Relationship: Correlation • 3 Conditions: • Quantitative Variable • Straight Enough: Could draw a line through the scatter plot well enough • No Outliers: Why?

Correlation Coefficient • Measure of the strength of linear relationship between 2 quantitative variables • • Between -1 and 1 “Weak” correlation: close to 0 “Strong Positive” correlation: close to 1 “Strong Negative” correlation: close to -1

Correlation Need to Know Facts • DOES NOT imply causation • Will be affected by the introduction of an outlier • Magnitude (or how far away from 0) will decrease • Direction (or whether it is + or –) will not change • • Will not be affected by standardization (turning data into z scores) Will not be affected if data recorded in different units Correlation has no units: Why? There may exist a strong non-linear relationship between variables…correlation does not measure this and could be close to 0 in this case

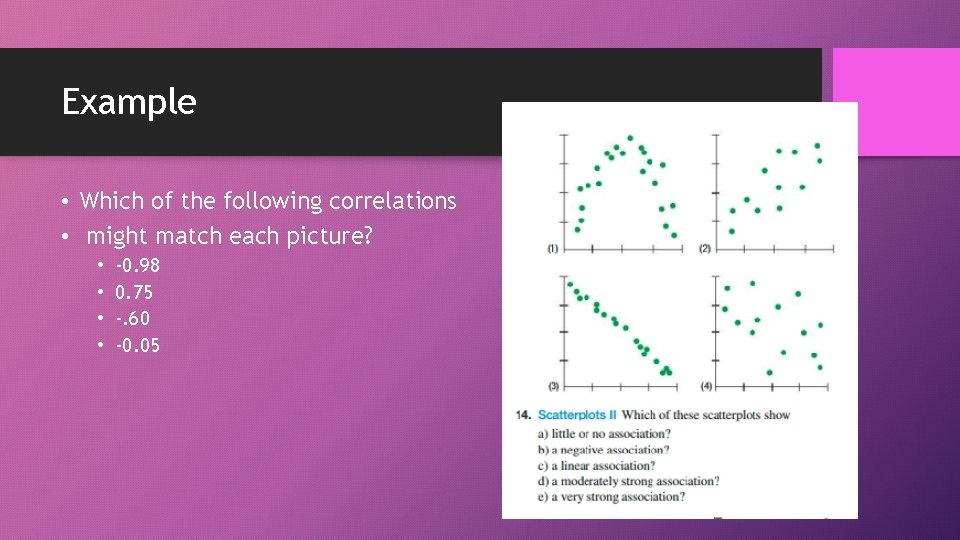
Example • Which of the following correlations • might match each picture? • • -0. 98 0. 75 -. 60 -0. 05

Example

Chapter 7: Linear Regression • Recall formulas for a line from algebra: • Slope intercept form • Point slope form • Standard form • How would we draw a line here: • How would we write a formula for that line?

Least Square’s: Line of best fit • First, we assume that a line is a good model for our data • Then, we estimate a slope and y intercept • We have formulas based on method of “least squares” • We want the smallest sum of squared “residuals” • Residual = Observed Value – Predicted Value

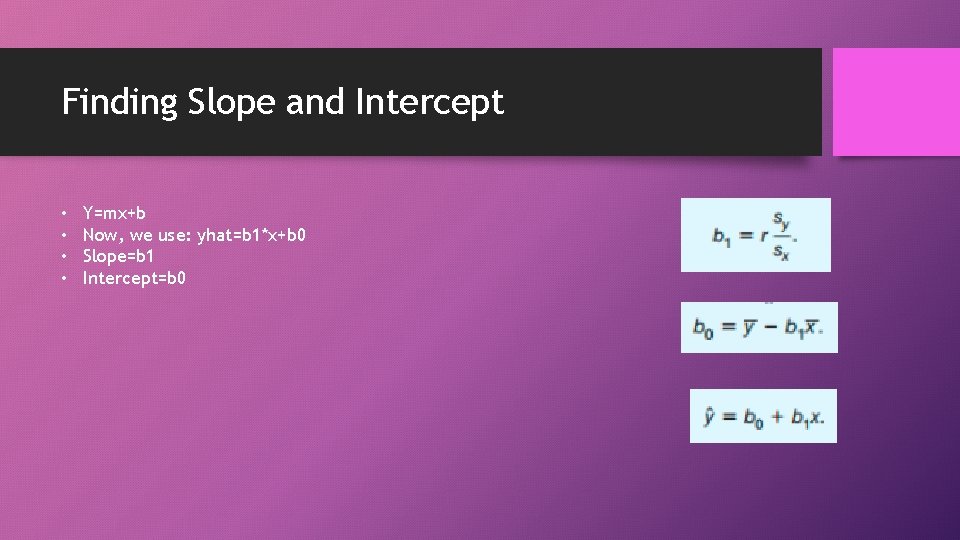
Finding Slope and Intercept • • Y=mx+b Now, we use: yhat=b 1*x+b 0 Slope=b 1 Intercept=b 0

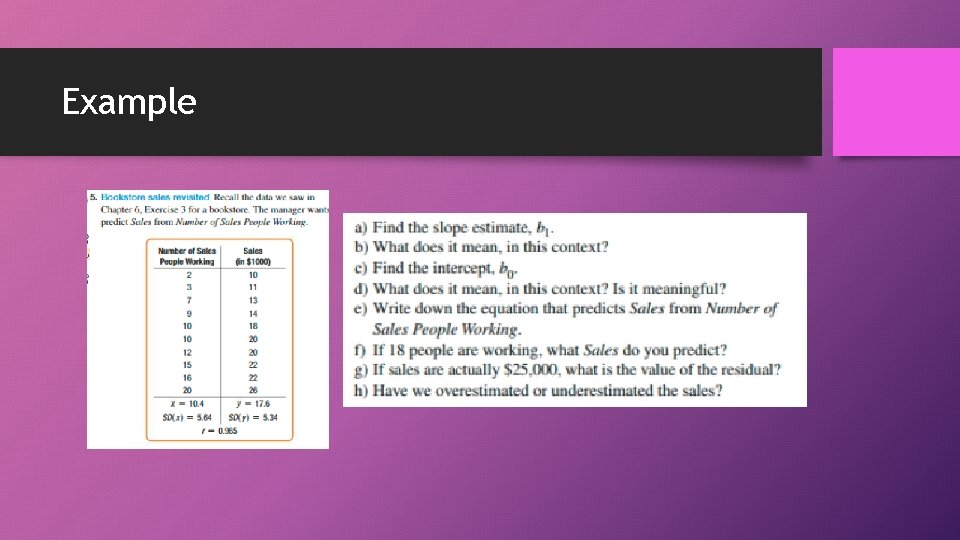
Example

Residual: Observed – Predicted Value • A measure of how well the model fits the data • Recall: “least square’s” method in particular reduces the sum of the squared residuals of all data points

Example Continued

R squared: Variation accounted for by the model • R squared = r^2, where r is the correlation coefficient • R squared is between 0 and 1. • High R squared means a large portion of the variation in y is accounted for by your linear regression model

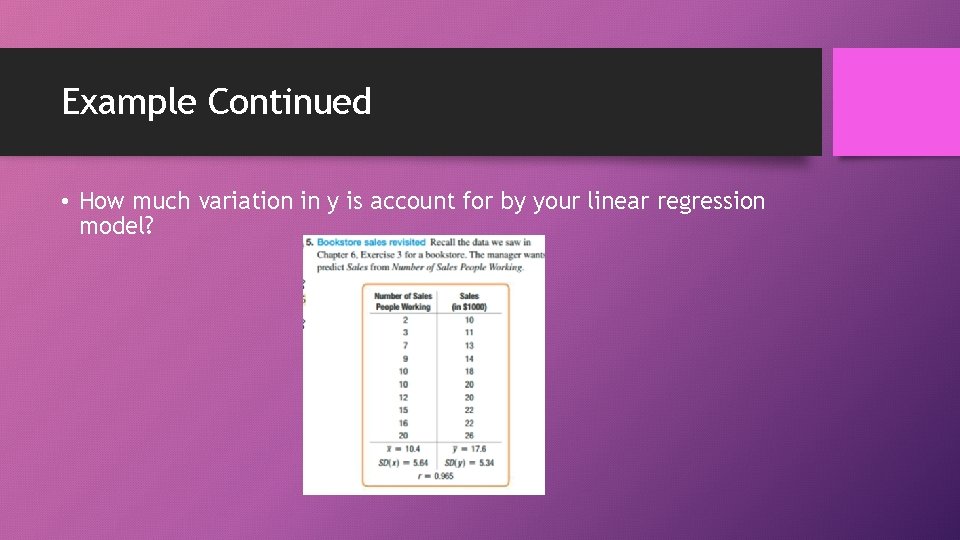
Example Continued • How much variation in y is account for by your linear regression model?

Assumptions needed for Linear Regression • Same as that of correlation: • • Quantitative Variable Straight Enough No outliers PLUS Equal spread across all values of x

After fitting your model • Check the residuals • Are the residuals centered around 0 • Do the residuals have equal spread • QQ plot: Do the residuals seem to follow a normal distribution

Quiz Today • • Correlation from scatterplot R^2 from correlation Z score 2 empirical rule problems

Review for Exam 1 • Review posted: https: //www. math. uic. edu/coursepages/stat 101/exams • Review Sessions: By popular demand • Wednesday, 5 -6 in Math and Science Learning Center • Thursday, 11 -12 in Math and Science Learning Center • Normal Office Hours: Tuesday 11 -12: 50 in Math and Science L. C. • Start studying now!

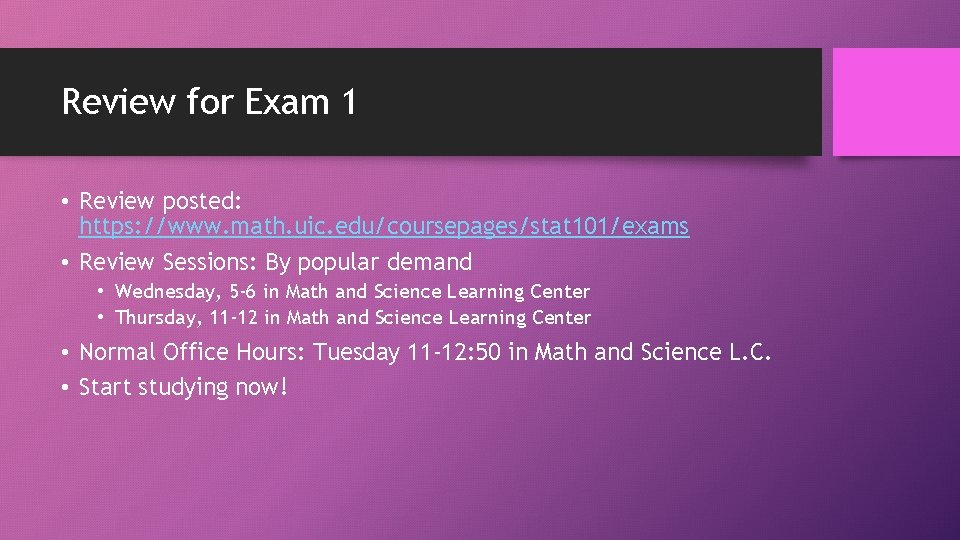
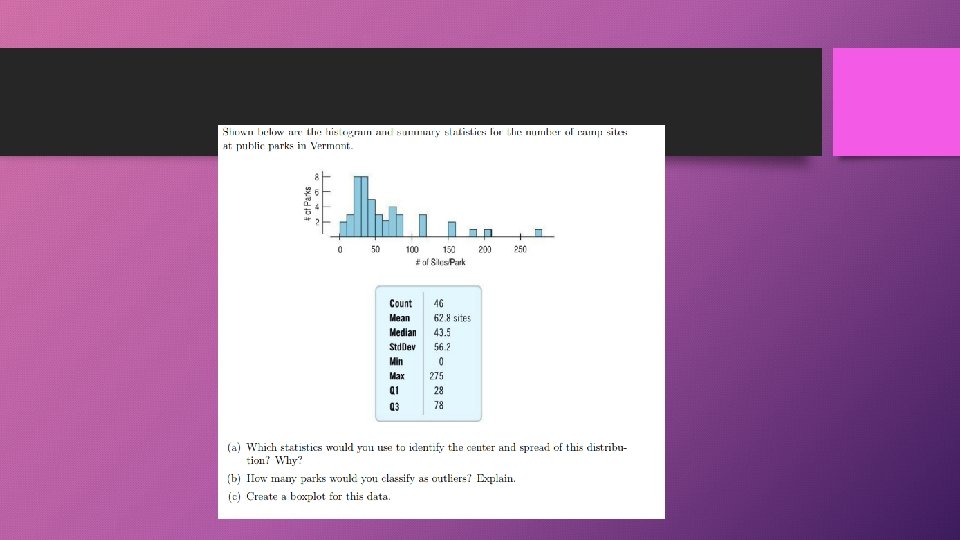
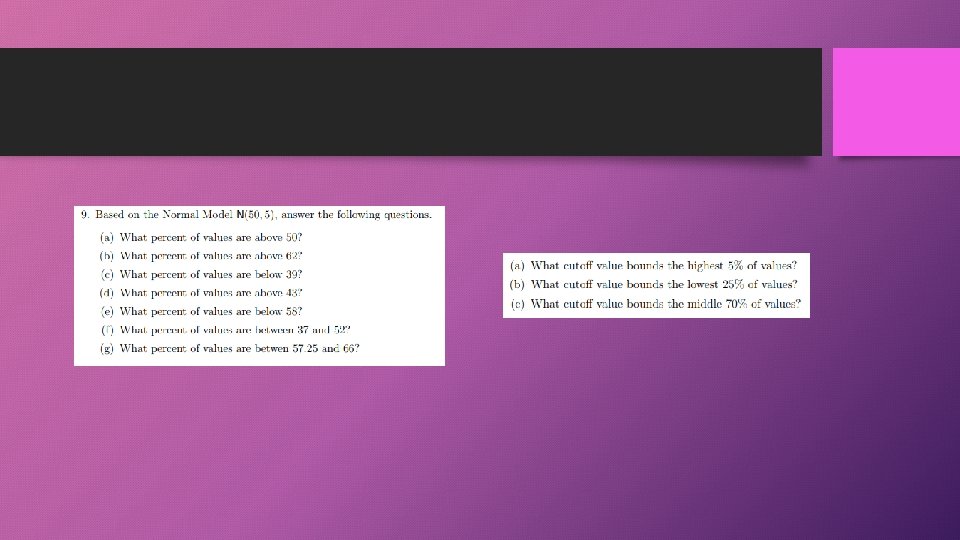
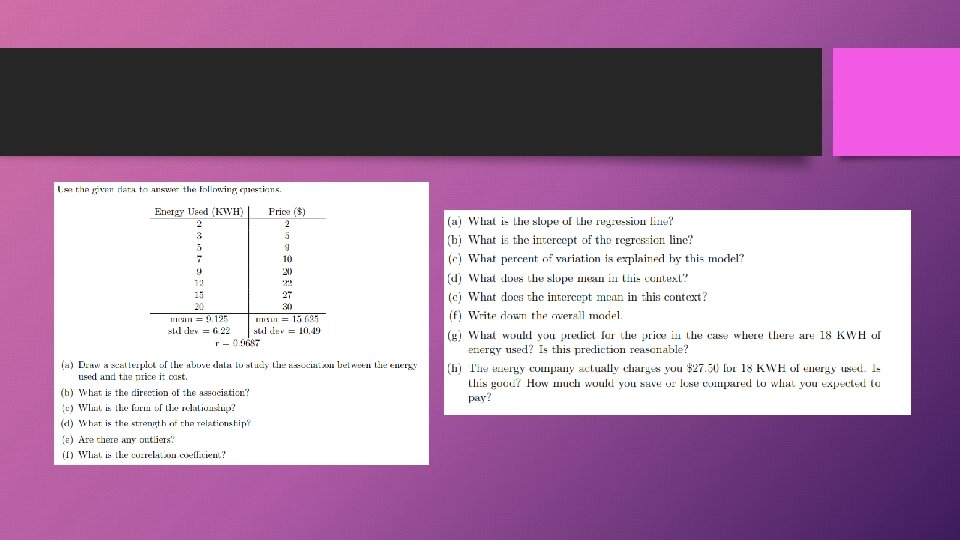
A couple questions from review