Correcting the Dynamic Call Graph Using Control Flow

Motivation l Complexity of large object oriented programs q q l Decompose the program

Inaccurate call graph b 1, 000 call b a call c Error method a

Call stack Timer-based sampling and timing bias 4 …c b cc b a cc

Call stack Timer-based sampling and timing bias 5 …c b cc b a cc

Call stack Timer-based sampling and timing bias 6 …c b cc b a cc

Call stack Timer-based sampling and timing bias 7 …c b cc b a cc

Timer-based sampling and timing bias DCGSample Call stack timer tick 8 …c … timer

Overhead and accuracy in call graph profiling Full instrumentation Overhead (%) 25 20 15

Outline l l l 10 Motivation Call graph correction Evaluation

Timing bias in SPEC JVM 98 raytrace Normalized frequency(%) Sampling Method calls grouped by

Normalized frequency(%) Timing bias in SPEC JVM 98 raytrace Method calls grouped by source

Correction algorithms l Detect and correct DCG error q l DCG constraint Static and

Static FDOM constraint l FDOM constraint on CFG q q l call c is

Static FDOM correction FDOM constraint: f( b 1, 000 a 500 c DCGSample l

Outline l l l 19 Motivation Call graph correction Evaluation

Experimental methodology l l Jikes RVM 2. 4. 5 on 3. 2 G Pentium

Summary l l l CFG constraint improves the DCG Inlining has been tuned for

Timing bias misleads optimizer 5, 000 times a 10, 000 times b c Sampling

Call graph profiling in online optimization system Source program Compile & instrument Machine code

Slides: 31

Download presentation

Correcting the Dynamic Call Graph Using Control Flow Constraints Byeongcheol (BK) Lee Kevin Resnick Michael Bond Kathryn Mc. Kinley UT Austin 1

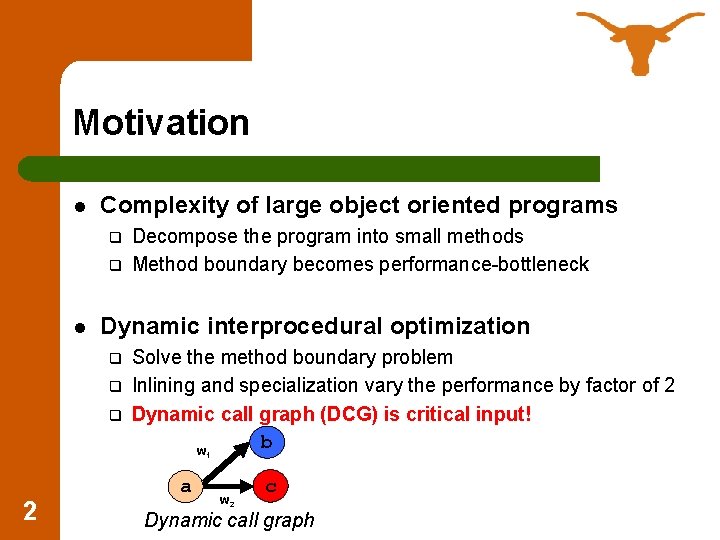
Motivation l Complexity of large object oriented programs q q l Decompose the program into small methods Method boundary becomes performance-bottleneck Dynamic interprocedural optimization q q q Solve the method boundary problem Inlining and specialization vary the performance by factor of 2 Dynamic call graph (DCG) is critical input! b w 1 2 a w 2 c Dynamic call graph

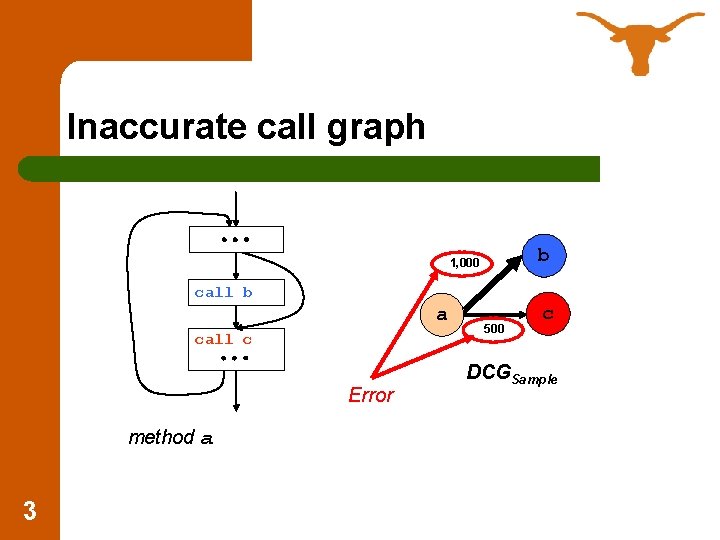
Inaccurate call graph b 1, 000 call b a call c Error method a 3 500 c DCGSample

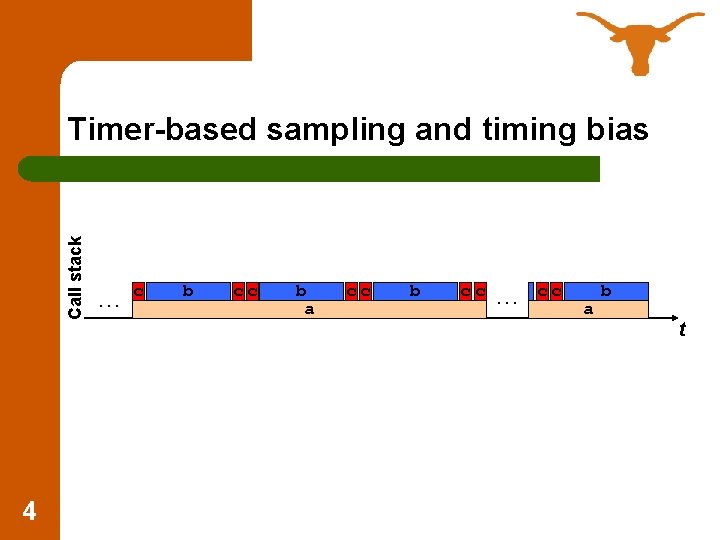
Call stack Timer-based sampling and timing bias 4 …c b cc b a cc b cc … cc a b t

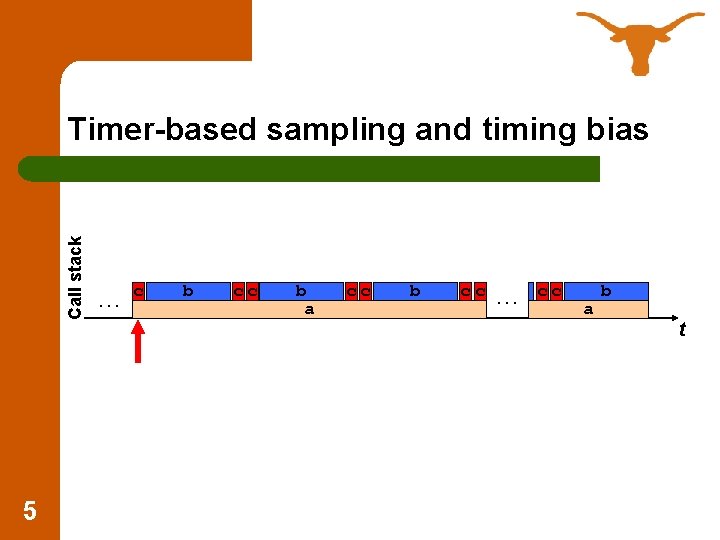
Call stack Timer-based sampling and timing bias 5 …c b cc b a cc b cc … cc a b t

Call stack Timer-based sampling and timing bias 6 …c b cc b a cc b cc … cc a b t

Call stack Timer-based sampling and timing bias 7 …c b cc b a cc b cc … cc a b t

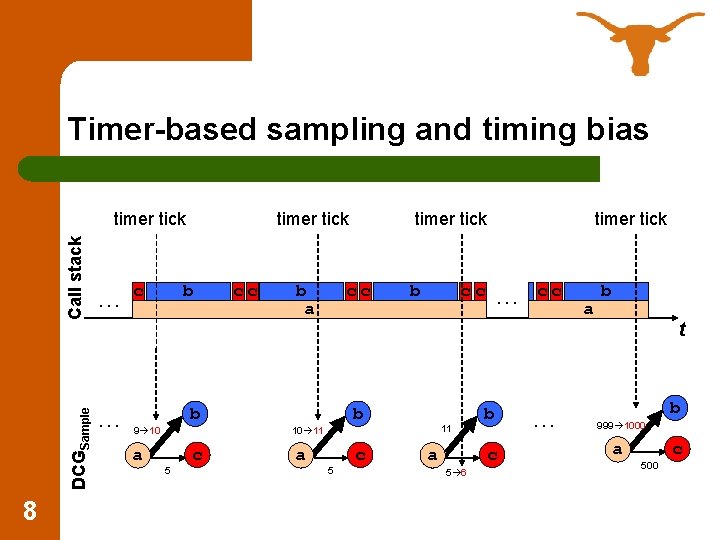
Timer-based sampling and timing bias DCGSample Call stack timer tick 8 …c … timer tick b cc b a cc b 9 10 a timer tick b cc b 11 10 11 5 c a 5 c timer tick … b c a 5 6 cc … a b t b 999 1000 c a 500

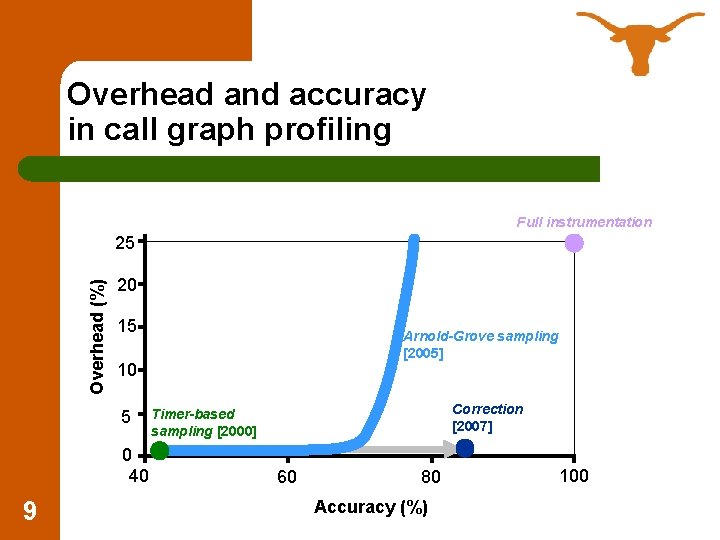
Overhead and accuracy in call graph profiling Full instrumentation Overhead (%) 25 20 15 10 5 0 40 9 Arnold-Grove sampling [2005] Correction [2007] Timer-based sampling [2000] 60 80 Accuracy (%) 100

Outline l l l 10 Motivation Call graph correction Evaluation

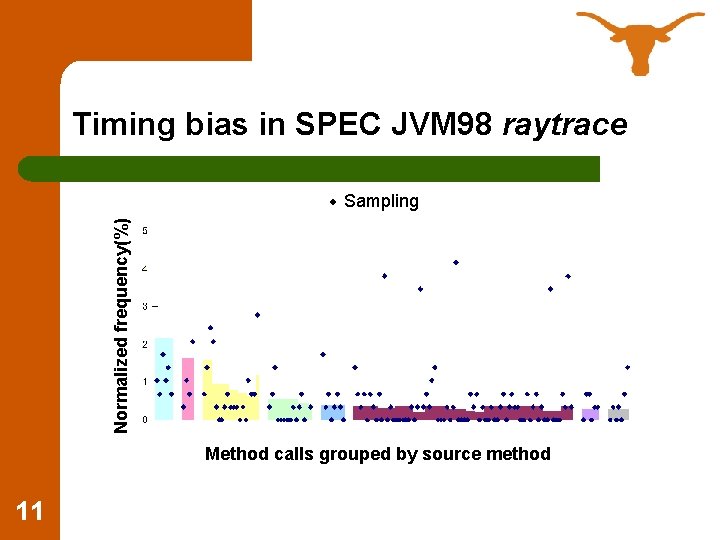
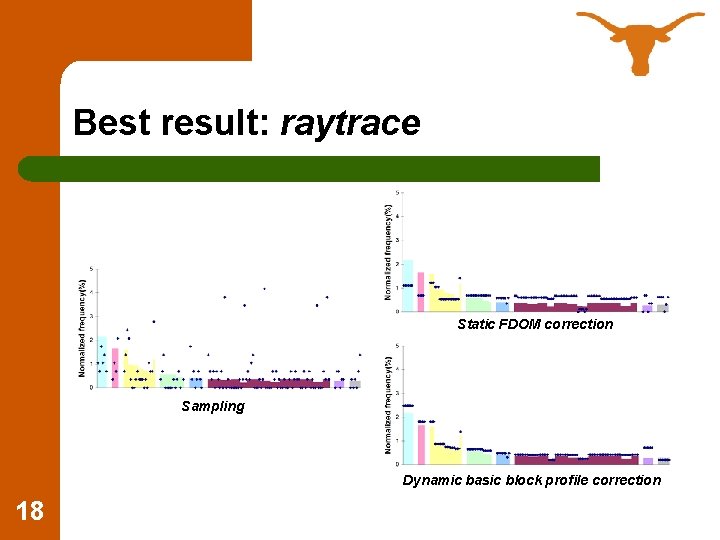
Timing bias in SPEC JVM 98 raytrace Normalized frequency(%) Sampling Method calls grouped by source method 11

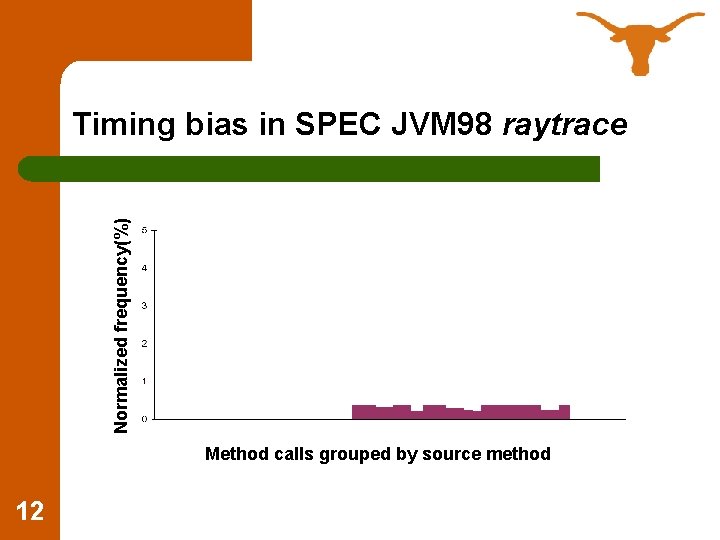
Normalized frequency(%) Timing bias in SPEC JVM 98 raytrace Method calls grouped by source method 12

Correction algorithms l Detect and correct DCG error q l DCG constraint Static and dynamic approaches q New Static FDOM (Frequency dominator) correction l l q Dynamic basic block profile correction l l 13 Static approach Uses static FDOM constraint on DCG Dynamic approach Uses dynamic basic block profile constraint on DCG

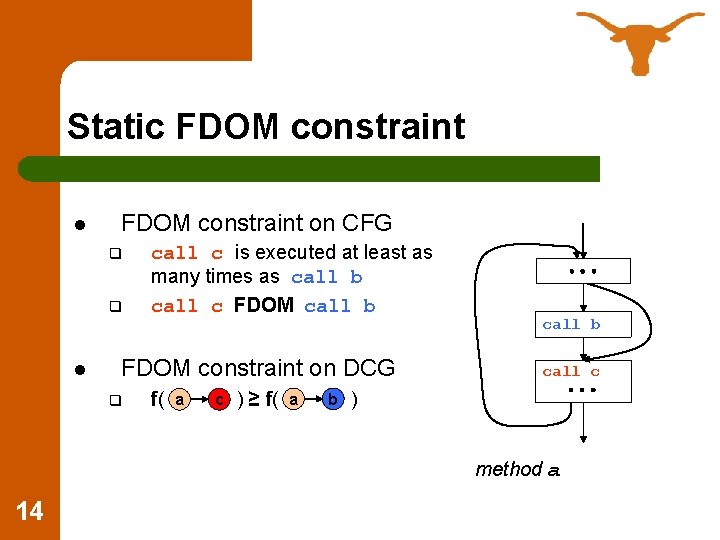
Static FDOM constraint l FDOM constraint on CFG q q l call c is executed at least as many times as call b call c FDOM call b FDOM constraint on DCG q f( a c ) ≥ f( a b call c ) method a 14

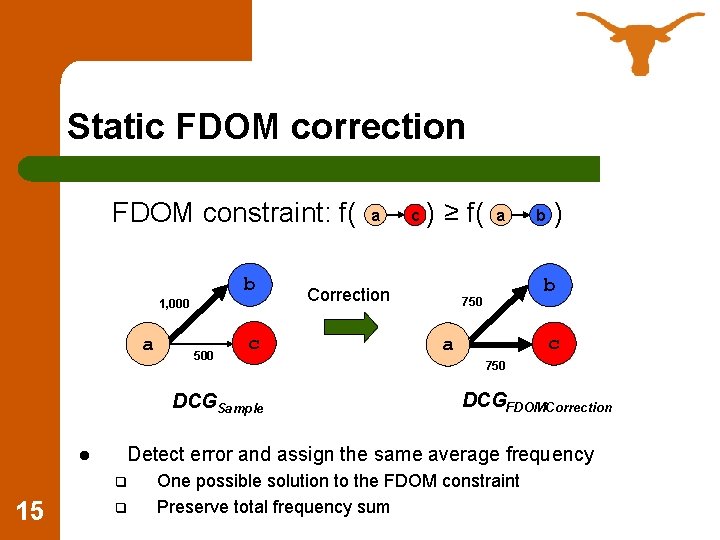
Static FDOM correction FDOM constraint: f( b 1, 000 a 500 c DCGSample l c ) ≥ f( Correction a b ) b 750 c a 750 DCGFDOMCorrection Detect error and assign the same average frequency q 15 a q One possible solution to the FDOM constraint Preserve total frequency sum

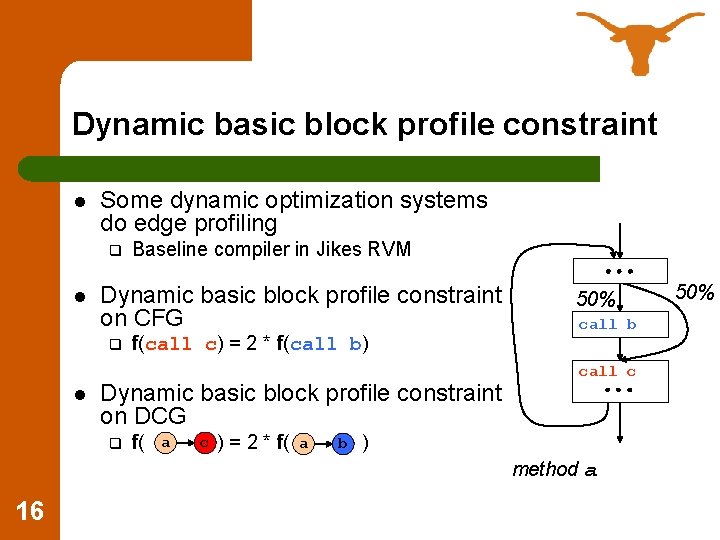
Dynamic basic block profile constraint l Some dynamic optimization systems do edge profiling q l Dynamic basic block profile constraint on CFG q l Baseline compiler in Jikes RVM f(call c) = 2 * f(call b) Dynamic basic block profile constraint on DCG q f( a c ) = 2 * f( a b 50% call b call c ) method a 16 50%

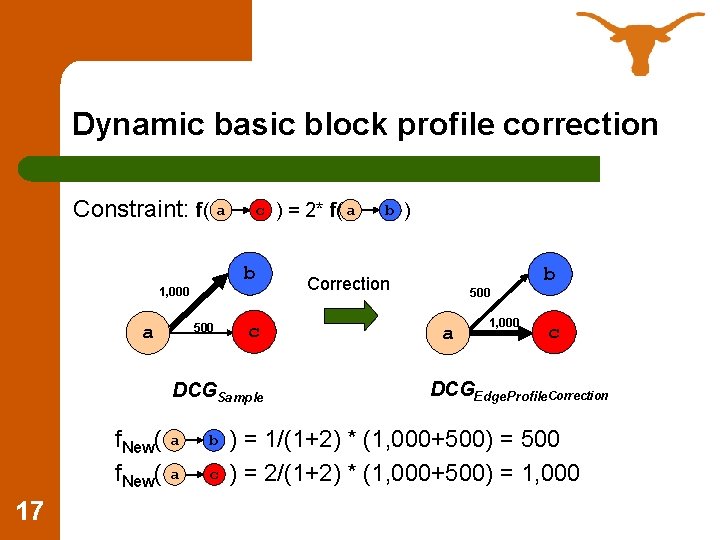
Dynamic basic block profile correction Constraint: f( a c b 1, 000 500 a c DCGSample f. New( a 17 b c ) = 2* f( a b ) b Correction 500 a 1, 000 c DCGEdge. Profile. Correction ) = 1/(1+2) * (1, 000+500) = 500 ) = 2/(1+2) * (1, 000+500) = 1, 000

Best result: raytrace Static FDOM correction Sampling Dynamic basic block profile correction 18

Outline l l l 19 Motivation Call graph correction Evaluation

Experimental methodology l l Jikes RVM 2. 4. 5 on 3. 2 G Pentium 4 Replay methodology [Blackburn et al. ‘ 06] q q q l Deterministic run 1 st iteration – compilation + application run 2 nd iteration – application run Measurement q Accuracy l q Overhead l q 20 1 st iteration includes call graph correction Performance l l Use overlap accuracy [Arnold & Grove ’ 05] 2 nd iteration is application-only SPECJVM 98 and Da. Capo benchmarks

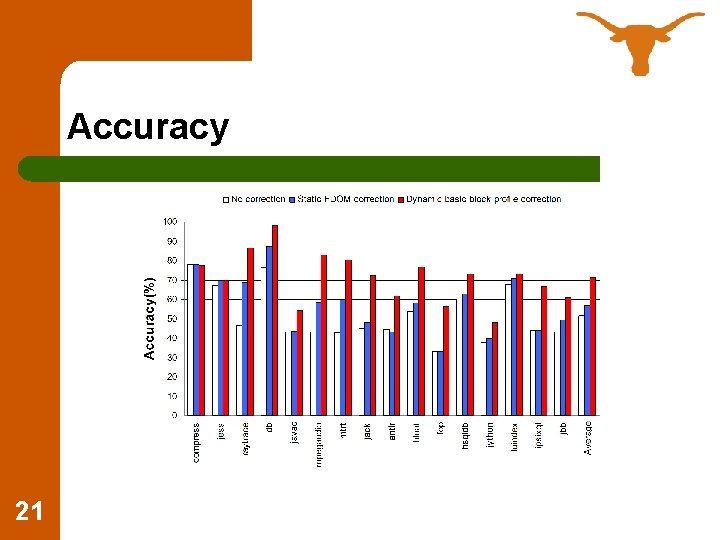
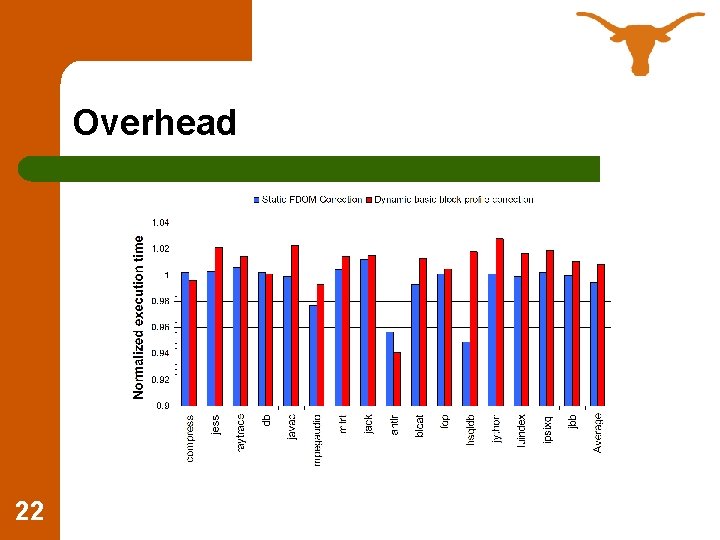
Accuracy 21

Overhead 22

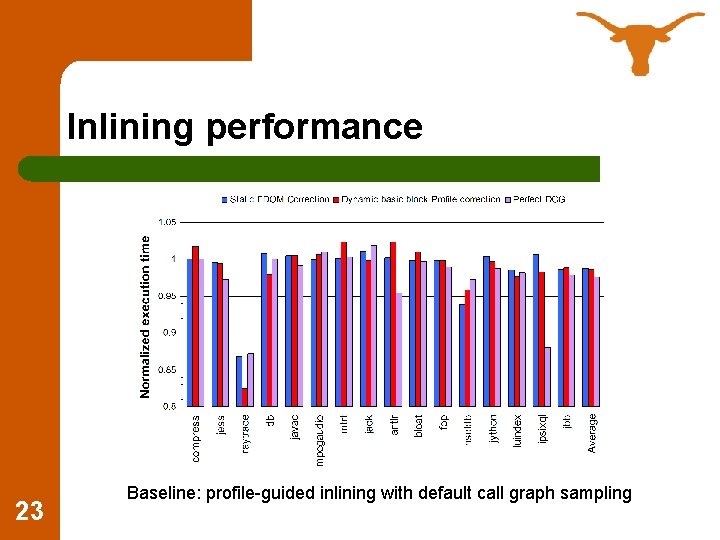
Inlining performance 23 Baseline: profile-guided inlining with default call graph sampling

Summary l l l CFG constraint improves the DCG Inlining has been tuned for bad call graph Advantages Can be easily combined with other DCG profiling q Minimal overhead only during the compilation q l Future work q 24 More inter-procedural optimizations with high accuracy DCG

Question and comment l 25 Thank you!

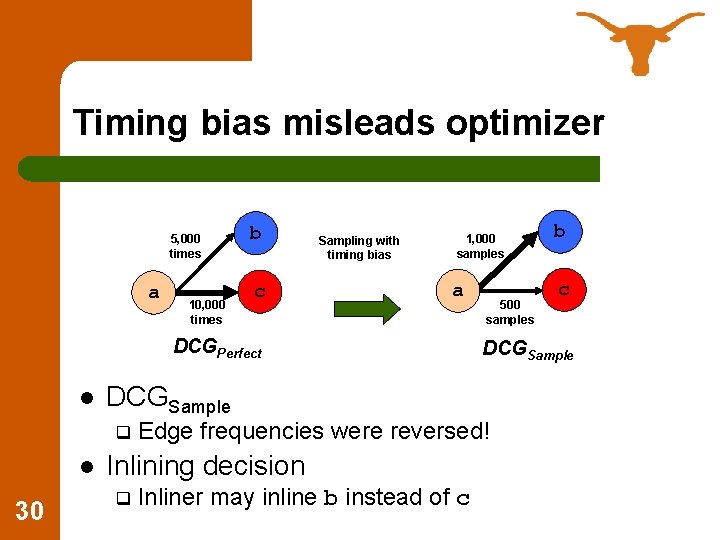
Timing bias misleads optimizer 5, 000 times a 10, 000 times b c Sampling with timing bias 1, 000 samples a DCGPerfect l DCGSample q l 30 Inliner may inline b instead of c c DCGSample Edge frequencies were reversed! Inlining decision q 500 samples b

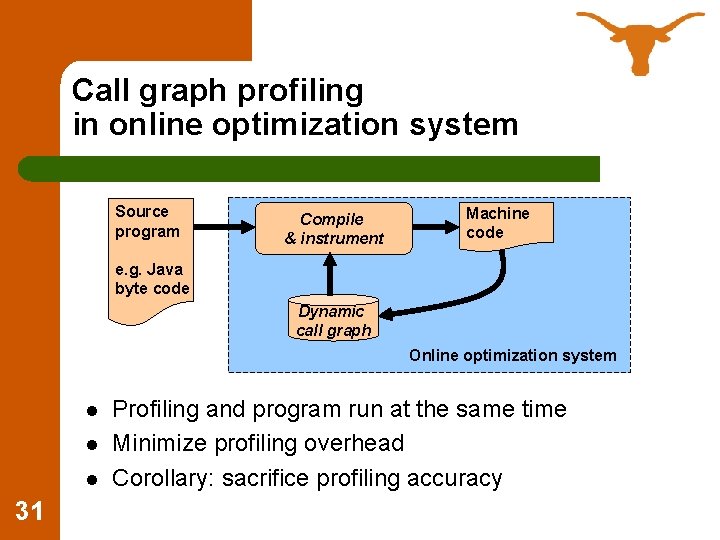
Call graph profiling in online optimization system Source program Compile & instrument Machine code e. g. Java byte code Dynamic call graph Online optimization system l l l 31 Profiling and program run at the same time Minimize profiling overhead Corollary: sacrifice profiling accuracy