Core Pure 2 Chapter 2 Series jfrosttiffin kingston

Core. Pure 2 Chapter 2 : : Series jfrost@tiffin. kingston. sch. uk www. drfrostmaths. com @Dr. Frost. Maths Last modified: 7 th August 2018

www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including MAT + UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Questions organised by topic, difficulty and past paper. Teaching videos with topic tests to check understanding.

Chapter Overview Those who have done either IGCSE Mathematics, IGCSE Further Mathematics or Additional Mathematics would have encountered this content. Otherwise it will be completely new! 1: : Method of differences 2: : Maclaurin Expansions 3: : Maclaurin Expansions for Composite Functions Teacher Note: This is just the two old FP 2 chapters on Method of Differences and Maclaurin Expansions/Taylor Series has been moved to (the new) FP 1.

STARTER – Round 1! ? ?

STARTER – Round 2! Fro Hint: Perhaps write out the first few terms? ?

Example ? ? Carefully look at the pattern of cancelling. The second term in each pair is cancelled out by the first term in the previous pair. Thus in the last pair the first term won’t have been cancelled out. While not essential, I like to put brackets around pairs to see the exact matchings more easily.

Partial Fraction Example ? ? ?

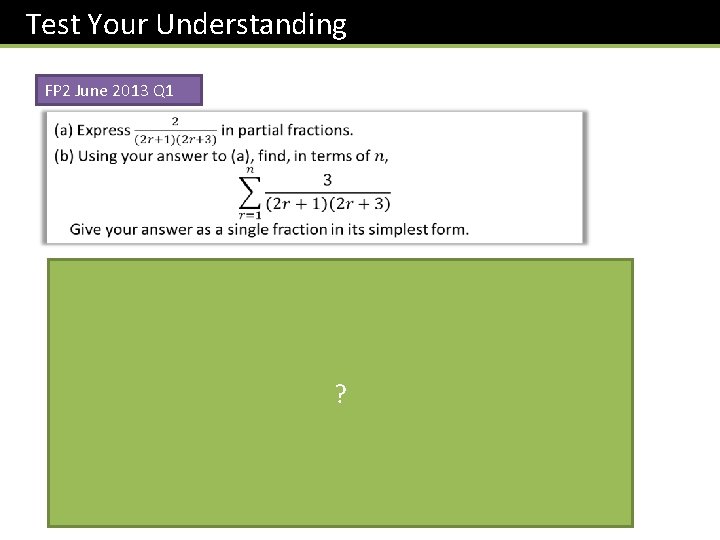
Test Your Understanding FP 2 June 2013 Q 1 ?

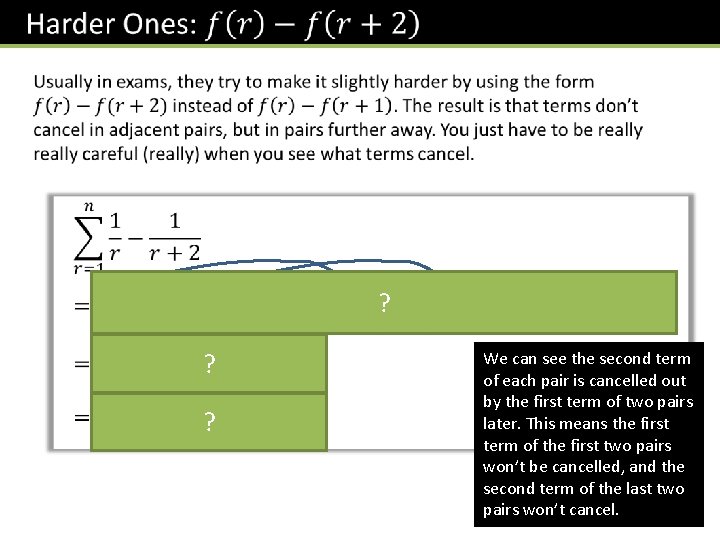
? ? ? We can see the second term of each pair is cancelled out by the first term of two pairs later. This means the first term of the first two pairs won’t be cancelled, and the second term of the last two pairs won’t cancel.

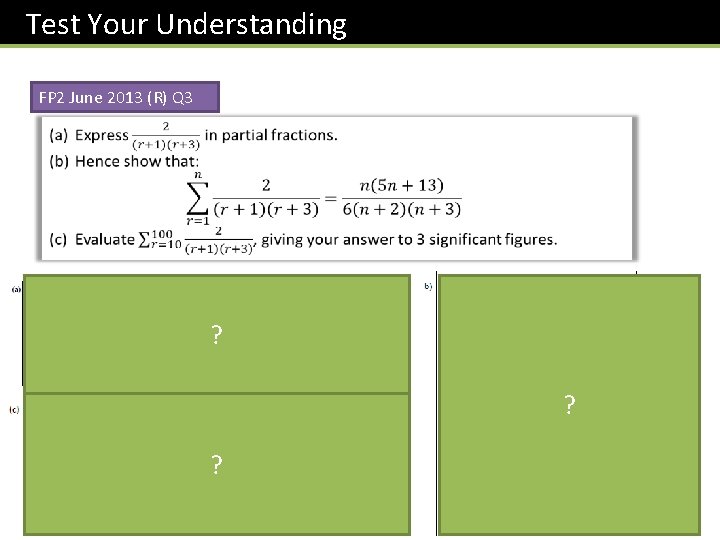
Test Your Understanding FP 2 June 2013 (R) Q 3 ? ? ?

Exercise 2 A Pearson Core Pure Year 2 Pages 36 -37 Note: This exercise has few examples of the “differ by 2” type questions that were extremely common in the old FP 2 exams. I have a compilation of exam questions on this topic here: https: //www. drfrostmaths. com/resource. php? rid=19

Higher Derivatives Original Function Lagrange’s Notation Leibniz’s Notation Newton’s Notation 1 st Derivative 2 nd Derivative ? ? ? ? ? It’s a bit derivative. Joke used with kind permission of Frost Jokes Ltd.

Examples ? ?

Why we might represent functions as power series Example: Reasons why this is awesome 1 2 3

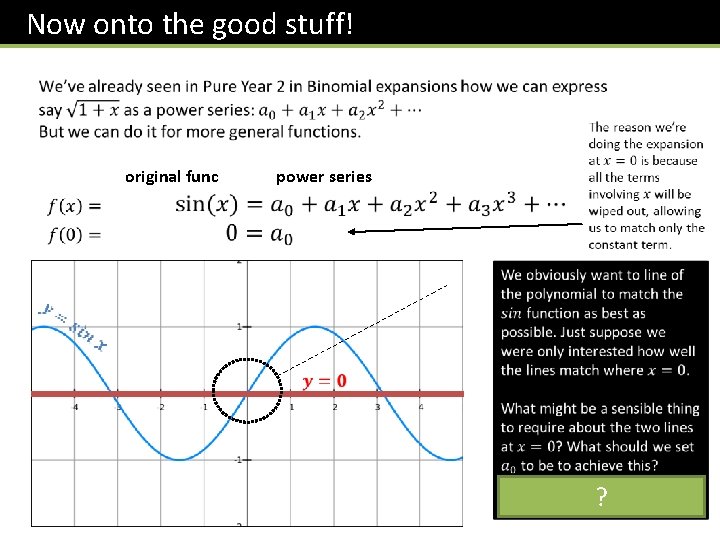
Now onto the good stuff! original func power series ?

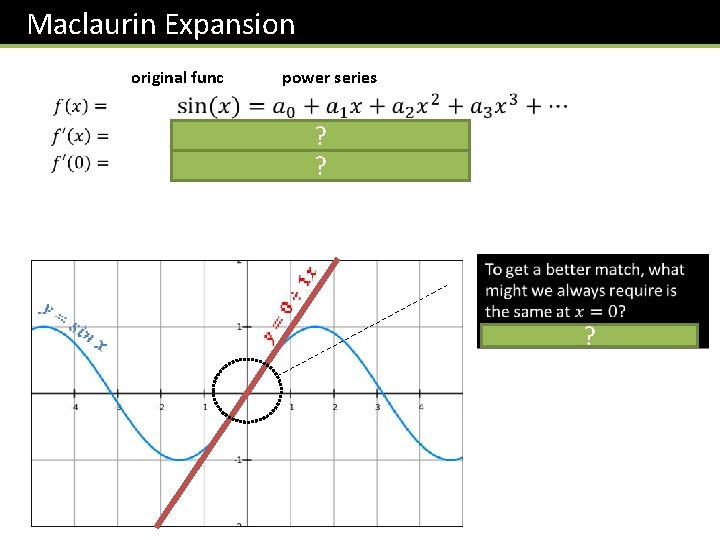
Maclaurin Expansion original func power series ? ?

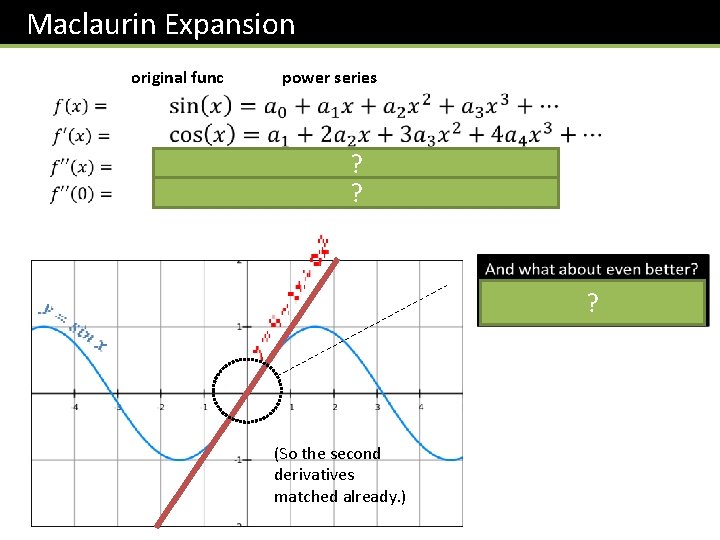
Maclaurin Expansion original func power series ? ? ? (So the second derivatives matched already. )

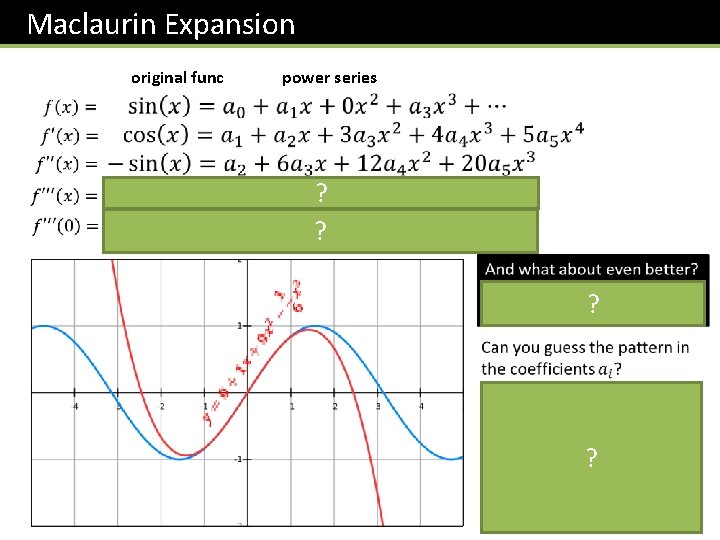
Maclaurin Expansion original func power series ? ? ? ?

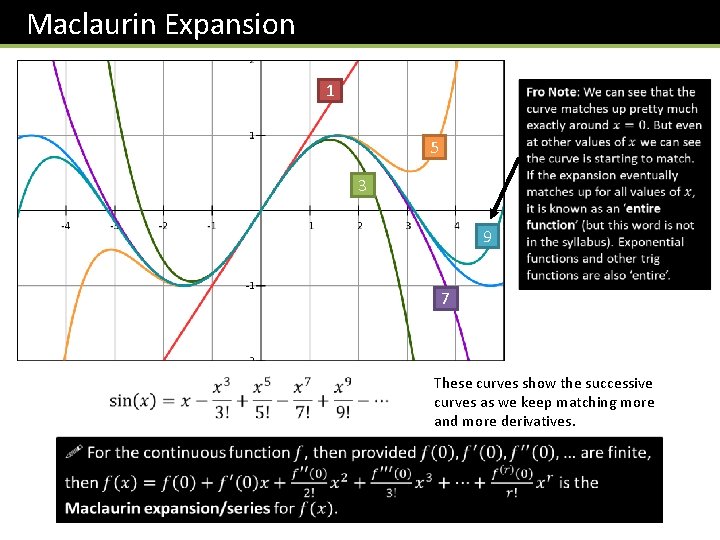
Maclaurin Expansion 1 5 3 9 7 These curves show the successive curves as we keep matching more and more derivatives.

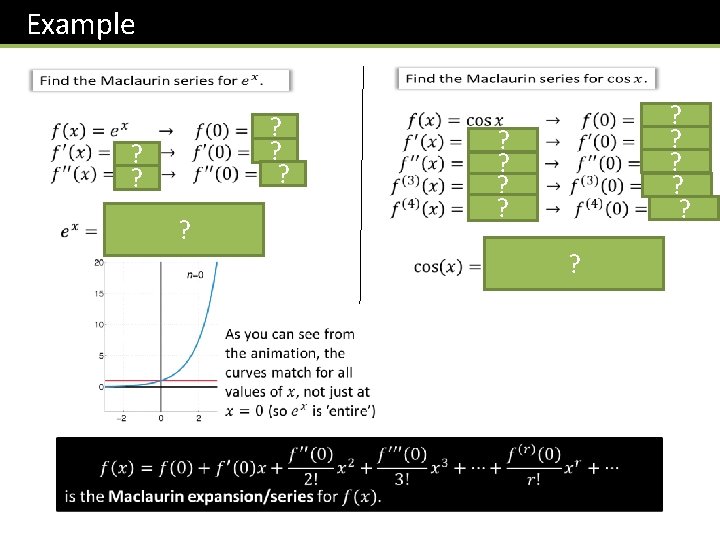
Example ? ? ? ?

Example ? ? ? ? ?

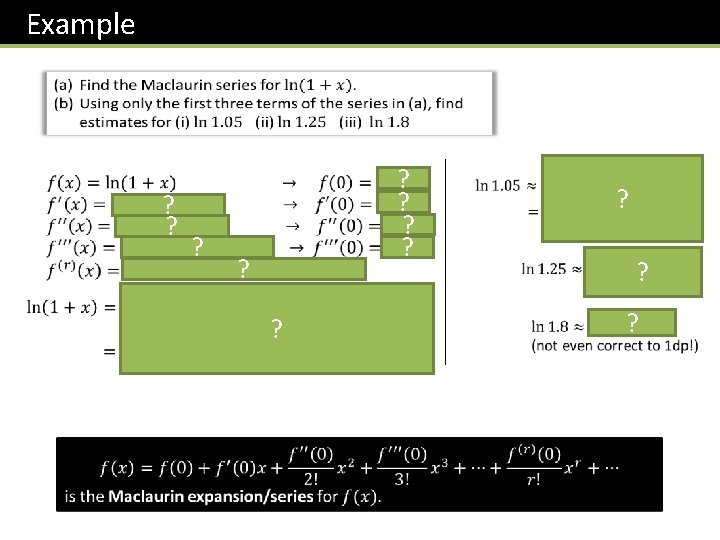
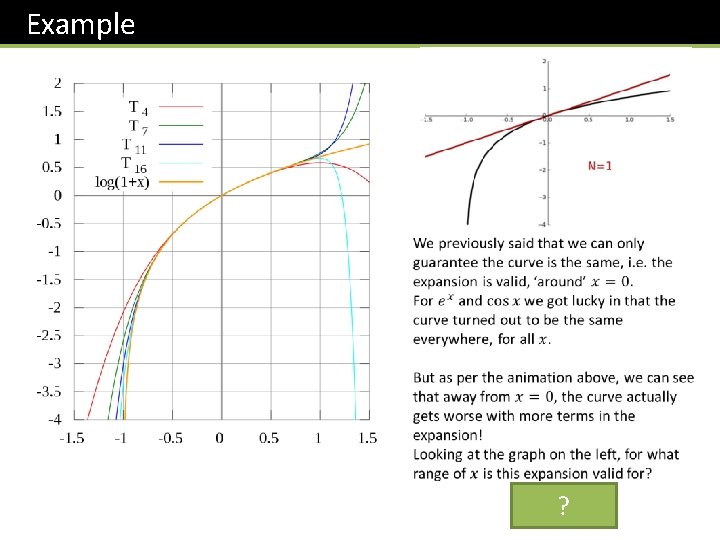
Example ?

Exercise 2 C Pearson Core Pure Year 2 Page 43 -44

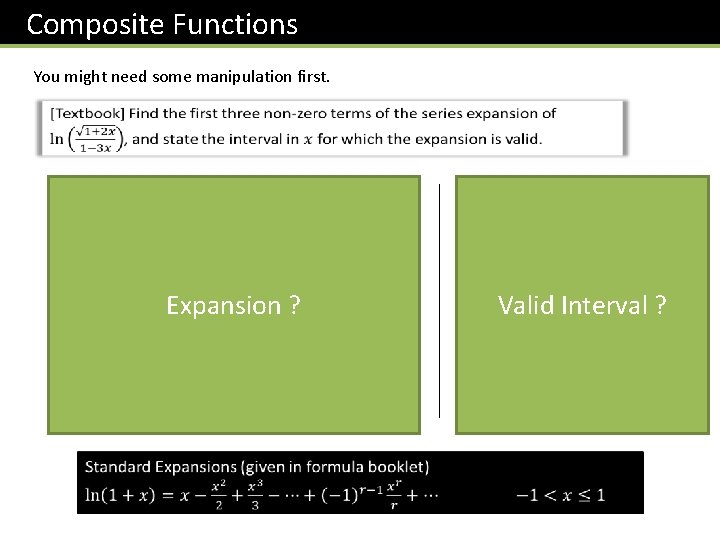
Composite Functions We can also apply these when the input to the function is different. ?

Composite Functions You might need some manipulation first. Expansion ? Valid Interval ?

Composite Functions ?

Exercise 2 D Pearson Core Pure Year 2 Page 46 -48