Core Pure 2 Chapter 1 Complex Numbers jfrosttiffin

Core. Pure 2 Chapter 1 : : Complex Numbers jfrost@tiffin. kingston. sch. uk www. drfrostmaths. com @Dr. Frost. Maths Last modified: 15 th February 2019
www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including MAT + UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Questions organised by topic, difficulty and past paper. Teaching videos with topic tests to check understanding.

OVERVIEW 1 : : Exponential form of a complex number 2 : : Multiplying and dividing complex numbers 4 : : De Moivre’s for Trigonometric Identities 5 : : Roots 3 : : De Moivre’s Theorem 6 : : Sums of series Note for teachers: Most of this content is the old FP 2, but sums of series is new.
![RECAP : : Modulus-Argument Form Im[z] ? Re[z] ? modulus ? argument ? ? RECAP : : Modulus-Argument Form Im[z] ? Re[z] ? modulus ? argument ? ?](http://slidetodoc.com/presentation_image/2ed5ac4e56c5e0310946cb3922b497ed/image-4.jpg)
RECAP : : Modulus-Argument Form Im[z] ? Re[z] ? modulus ? argument ? ? ? ?
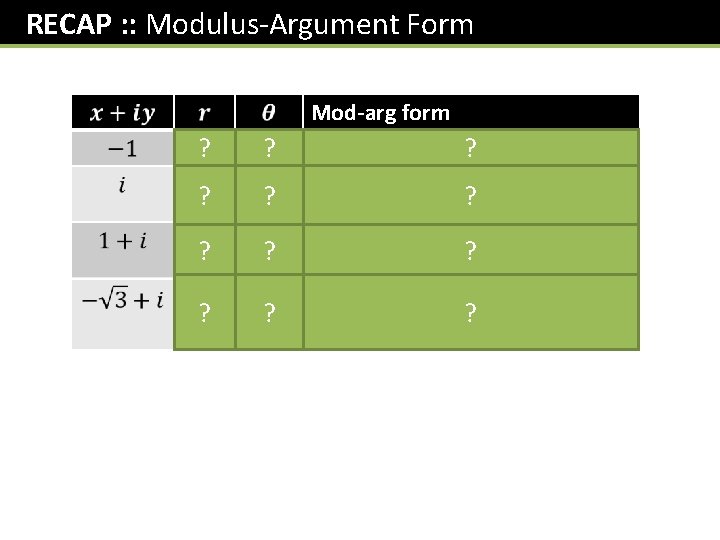
RECAP : : Modulus-Argument Form Mod-arg form ? ? ?

Exponential Form ? ? ? ?

Exponential Form You need to be able to convert to and from exponential form. Mod-arg form ? ? ? ? Exp Form ? ? ? To get Cartesian form, put in modulusargument form first. Notice this is not a principal argument.

A Final Example ?

Exercise 1 A Pearson Core Pure Year 2 Page 5

Multiplying and Dividing Complex Numbers ? ? i. e. If you multiply two complex numbers, you multiply the moduli and add the arguments, and if you divide them, you divide the moduli and subtract the arguments. ? ?

Examples 1 ? 2 ? 3 ?

Test Your Understanding Edexcel FP 2(Old) June 2013 Q 2 ? ?

Exercise 1 B Pearson Core Pure Year 2 Pages 7 -8

De Moivre’s Theorem We saw that: ? Edexcel FP 2(Old) June 2013 Q 4 They so went there. . . ? Secret Alternative Way ?

De Moivre’s Theorem for Exponential Form ?

Examples ? ?

Test Your Understanding Edexcel FP 2(Old) June 2010 Q 4 ? ?

Exercise 1 C Pearson Core Pure Year 2 Pages 10 -11

Applications of de Moivre #1: Trig identities ? ? ?

Applications of de Moivre #1: Trig identities
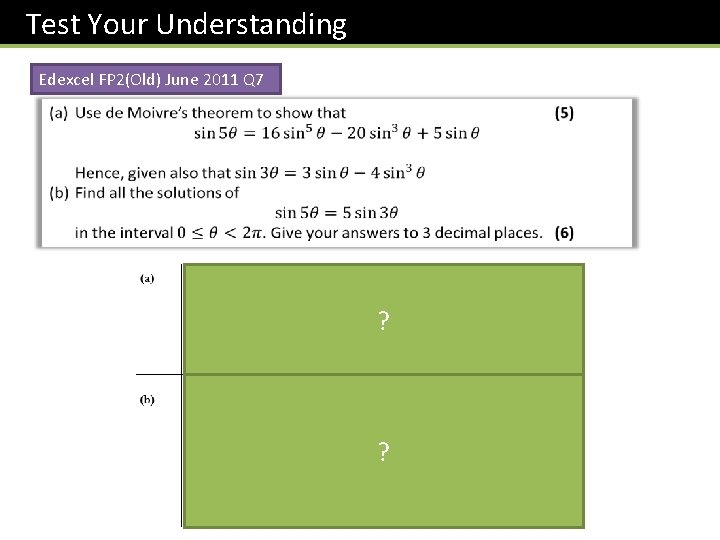
Test Your Understanding Edexcel FP 2(Old) June 2011 Q 7 ? ?


Starting point? ? Notice how the powers descend by 2 each time. ? ? Using identities below. ?

Starting point? ? Fro Speed Tip: Remember that terms in such an expansion oscillate between positive and negative. ? ? ? Again using identities.

Test Your Understanding Starting point? ?

Exercise 1 D Pearson Core Pure Year 2 Pages 14 -15

Sums of Series The formula for the sum of a geometric series also applies to complex numbers:
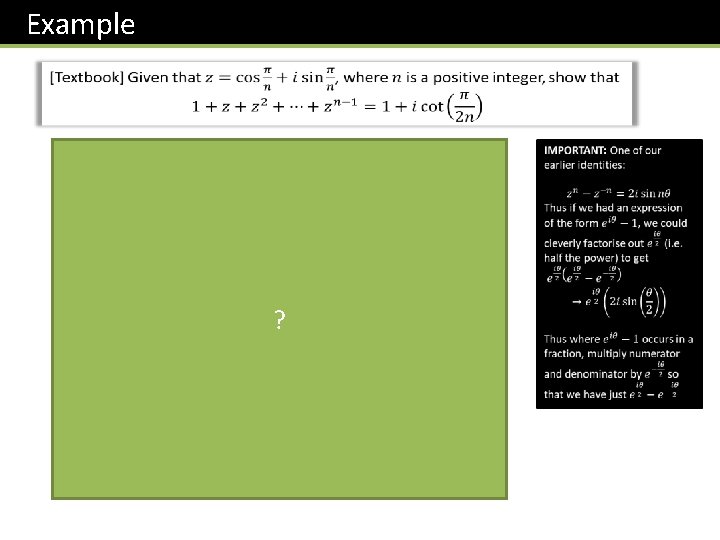
Example ?

Let’s practise that hard bit… ? ? ?

Using mod-arg form to split summation

Example a ?

Example b ?

Exercise 1 E Pearson Core Pure Year 2 Pages 18 -19

Applications of de Moivre #2: Roots Plot these roots on an Argand diagram. ? ? 1 is always a root – the rest are spread out equally distributed. We’ll see why we get this pattern on the next slide.

More on Roots of Unity
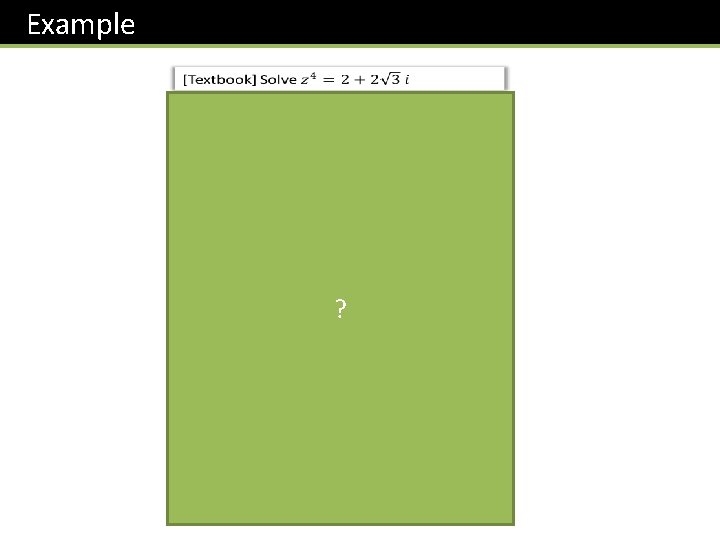
Example ?

Test Your Understanding Edexcel FP 2(Old) June 2012 Q 3 ? ?

Exercise 1 F Pearson Core Pure Year 2 Pages 24 -25
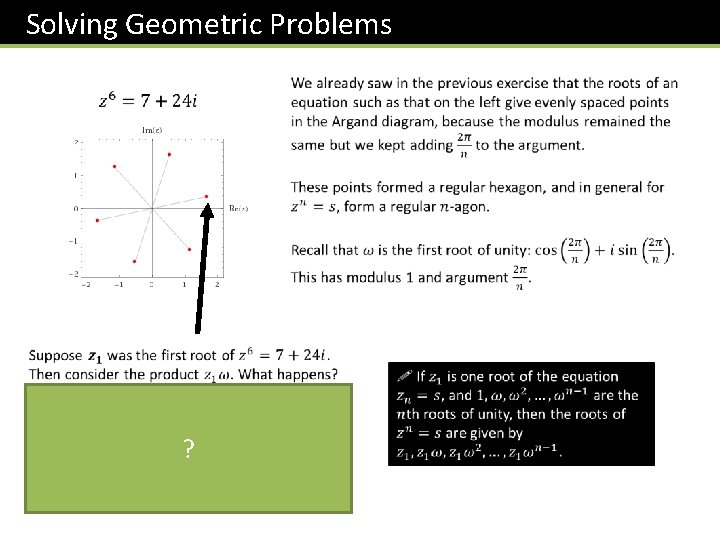
Solving Geometric Problems ?

Example a ? ? Diagram b ?

Exercise 1 G Pearson Core Pure Year 2 Pages 26 -27
- Slides: 41