Copyright 2005 Pearson Education Inc Chapter 8 Complex













































- Slides: 54

Copyright © 2005 Pearson Education, Inc.

Chapter 8 Complex Numbers, Equations Copyright © 2005 Pearson Education, Inc. Polar Equations, and Parametric

8. 1 Complex Numbers Copyright © 2005 Pearson Education, Inc.

Basic Concepts n n n and i is the imaginary unit Numbers in the form a + bi are called complex numbers q q a is the real part b is the imaginary part Copyright © 2005 Pearson Education, Inc. Slide 8 -4

Examples n a) n c) n d) Copyright © 2005 Pearson Education, Inc. b) e) Slide 8 -5

Example: Solving Quadratic Equations n Solve x = 25 Take the square root on both sides. n The solution set is { 5 i}. n Copyright © 2005 Pearson Education, Inc. Slide 8 -6

Another Example n Solve: x 2 + 54 = 0 n The solution set is Copyright © 2005 Pearson Education, Inc. Slide 8 -7

Example: Products and Quotients n Multiply: Copyright © 2005 Pearson Education, Inc. n Divide: Slide 8 -8

Addition and Subtraction of Complex Numbers n For complex numbers a + bi and c + di, n Examples (4 6 i) + ( 3 + 7 i) = [4 + ( 3)] + [ 6 + 7]i =1+i Copyright © 2005 Pearson Education, Inc. (10 4 i) (5 2 i) = (10 5) + [ 4 ( 2)]i = 5 2 i Slide 8 -9

Multiplication of Complex Numbers n For complex numbers a + bi and c + di, n The product of two complex numbers is found by multiplying as if the numbers were binomials and using the fact that i 2 = 1. Copyright © 2005 Pearson Education, Inc. Slide 8 -10

Examples: Multiplying n (2 4 i)(3 + 5 i) Copyright © 2005 Pearson Education, Inc. n (7 + 3 i)2 Slide 8 -11

Powers of i n i 1 = i i 5 = i i 9 = i n i 2 = 1 i 6 = 1 i 10 = 1 n i 3 = i i 7 = i i 11 = i n i 4 = 1 i 8 = 1 i 12 = 1 and so on. Copyright © 2005 Pearson Education, Inc. Slide 8 -12

Simplifying Examples n i 17 n i 4 = 1 i 17 = (i 4)4 • i = 1 • i =i Copyright © 2005 Pearson Education, Inc. Slide 8 -13

Property of Complex Conjugates For real numbers a and b, (a + bi)(a bi) = a 2 + b 2. n Example The product of a complex number and its conjugate is always a real number. Copyright © 2005 Pearson Education, Inc. Slide 8 -14

8. 2 Trigonometric (Polar) Form of Complex Numbers Copyright © 2005 Pearson Education, Inc.

Complex Plane n n We modify the familiar coordinate system by calling the horizontal axis the real axis and the vertical axis the imaginary axis. Each complex number a + bi determines a unique position vector with initial point (0, 0) and terminal point (a, b). Copyright © 2005 Pearson Education, Inc. Slide 8 -16

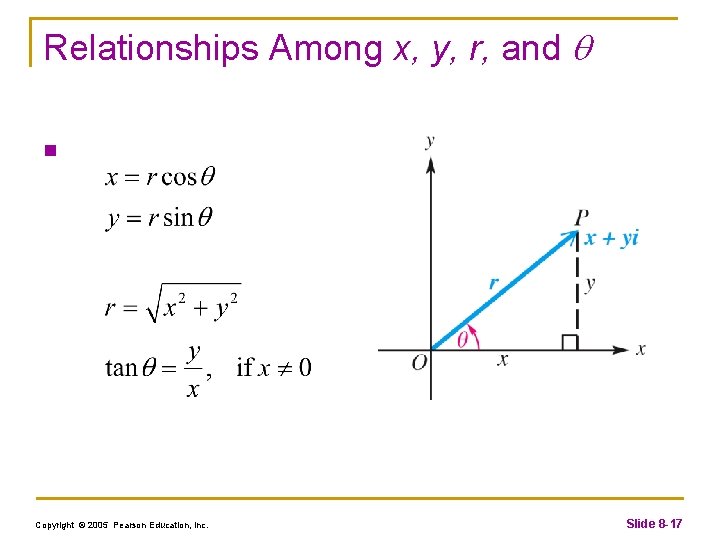
Relationships Among x, y, r, and n Copyright © 2005 Pearson Education, Inc. Slide 8 -17

Trigonometric (Polar) Form of a Complex Number n The expression is called the trigonometric form or (polar form) of the complex number x + yi. The expression cos + i sin is sometimes abbreviated cis . Using this notation Copyright © 2005 Pearson Education, Inc. Slide 8 -18

Example n Express 2(cos 120 + i sin 120 ) in rectangular form. n n Notice that the real part is negative and the imaginary part is positive, this is consistent with 120 degrees being a quadrant II angle. Copyright © 2005 Pearson Education, Inc. Slide 8 -19

Converting from Rectangular Form to Trigonometric Form n Step 1 Sketch a graph of the number x + yi in the complex plane. n Step 2 Find r by using the equation n Step 3 Find by using the equation choosing the quadrant indicated in Step 1. Copyright © 2005 Pearson Education, Inc. Slide 8 -20

Example n Example: Find trigonometric notation for 1 i. First, find r. n Thus, n Copyright © 2005 Pearson Education, Inc. Slide 8 -21

8. 3 The Product and Copyright © 2005 Pearson Education, Inc. Quotient Theorems

Product Theorem n If two complex numbers, then n In compact form, this is written Copyright © 2005 Pearson Education, Inc. are any Slide 8 -23

Example: Product n Find the product of Copyright © 2005 Pearson Education, Inc. Slide 8 -24

Quotient Theorem n If are any two complex numbers, where then Copyright © 2005 Pearson Education, Inc. Slide 8 -25

Example: Quotient n Find the quotient. Copyright © 2005 Pearson Education, Inc. Slide 8 -26

8. 4 De. Moivre’s Theorem; Numbers Copyright © 2005 Pearson Education, Inc. Powers and Roots of Complex

De Moivre’s Theorem n If is a complex number, and if n is any real number, then n In compact form, this is written Copyright © 2005 Pearson Education, Inc. Slide 8 -28

Example: Find ( 1 i)5 and express the result in rectangular form. n First, find trigonometric notation for 1 i n Theorem Copyright © 2005 Pearson Education, Inc. Slide 8 -29

nth Roots n For a positive integer n, the complex number a + bi is an nth root of the complex number x + yi if Copyright © 2005 Pearson Education, Inc. Slide 8 -30

nth Root Theorem n If n is any positive integer, r is a positive real number, and is in degrees, then the nonzero complex number r(cos + i sin ) has exactly n distinct nth roots, given by n where Copyright © 2005 Pearson Education, Inc. Slide 8 -31

Example: Square Roots n n Find the square roots of Trigonometric notation: For k = 0, root is For k = 1, root is Copyright © 2005 Pearson Education, Inc. Slide 8 -32

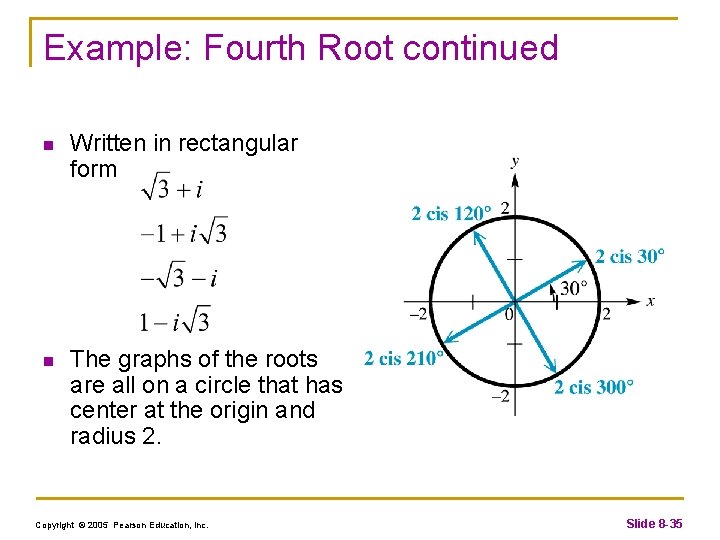
Example: Fourth Root n n n Find all fourth roots of roots in rectangular form. Write in trigonometric form. Write the Here r = 16 and = 120. The fourth roots of this number have absolute value Copyright © 2005 Pearson Education, Inc. Slide 8 -33

Example: Fourth Root continued n There are fourth roots, let k = 0, 1, 2 and 3. n Using these angles, the fourth roots are Copyright © 2005 Pearson Education, Inc. Slide 8 -34

Example: Fourth Root continued n Written in rectangular form n The graphs of the roots are all on a circle that has center at the origin and radius 2. Copyright © 2005 Pearson Education, Inc. Slide 8 -35

8. 5 Polar Equations and Graphs Copyright © 2005 Pearson Education, Inc.

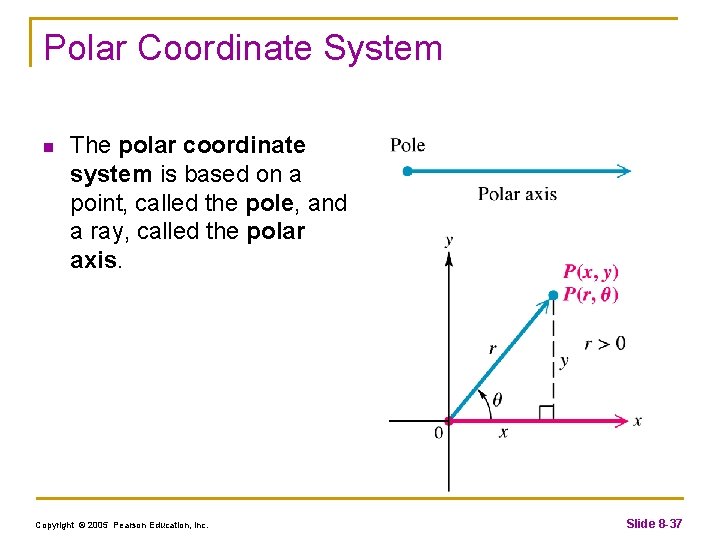
Polar Coordinate System n The polar coordinate system is based on a point, called the pole, and a ray, called the polar axis. Copyright © 2005 Pearson Education, Inc. Slide 8 -37

Rectangular and Polar Coordinates n If a point has rectangular coordinates (x, y) and polar coordinates (r, ), then these coordinates are related as follows. Copyright © 2005 Pearson Education, Inc. Slide 8 -38

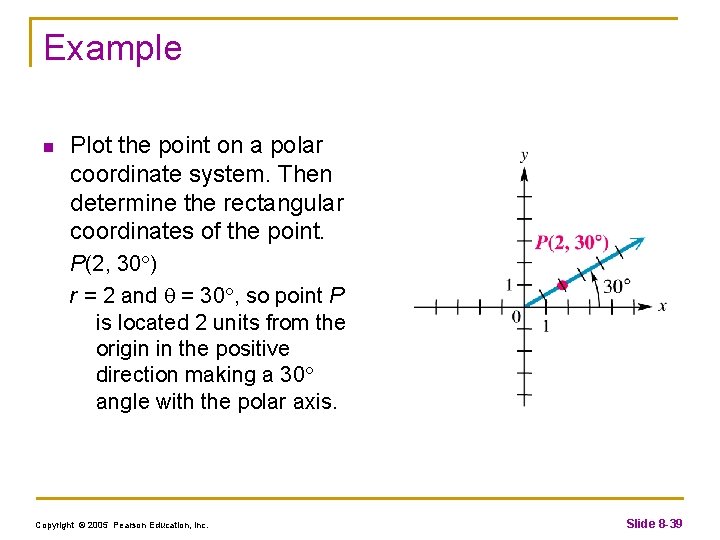
Example n Plot the point on a polar coordinate system. Then determine the rectangular coordinates of the point. P(2, 30 ) r = 2 and = 30 , so point P is located 2 units from the origin in the positive direction making a 30 angle with the polar axis. Copyright © 2005 Pearson Education, Inc. Slide 8 -39

Example n Convert (4, 2) to polar coordinates. Copyright © 2005 Pearson Education, Inc. Slide 8 -40

Rectangular and Polar Equations n To convert a rectangular equation into a polar equation, use and solve for r. Copyright © 2005 Pearson Education, Inc. Slide 8 -41

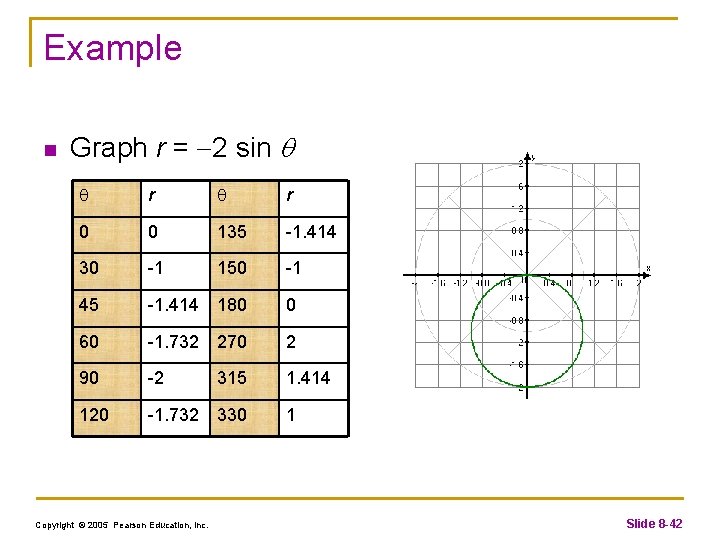
Example n Graph r = 2 sin r r 0 0 135 -1. 414 30 -1 150 -1 45 -1. 414 180 0 60 -1. 732 270 2 90 -2 1. 414 120 -1. 732 330 Copyright © 2005 Pearson Education, Inc. 315 1 Slide 8 -42

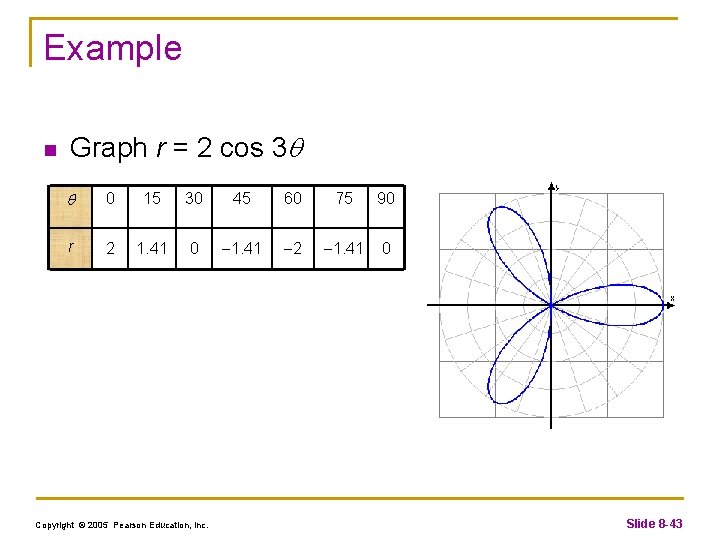
Example n Graph r = 2 cos 3 0 15 30 45 60 75 90 r 2 1. 41 0 1. 41 2 1. 41 0 Copyright © 2005 Pearson Education, Inc. Slide 8 -43

Example n Convert r = 3 cos sin into a rectangular equation. Copyright © 2005 Pearson Education, Inc. Slide 8 -44

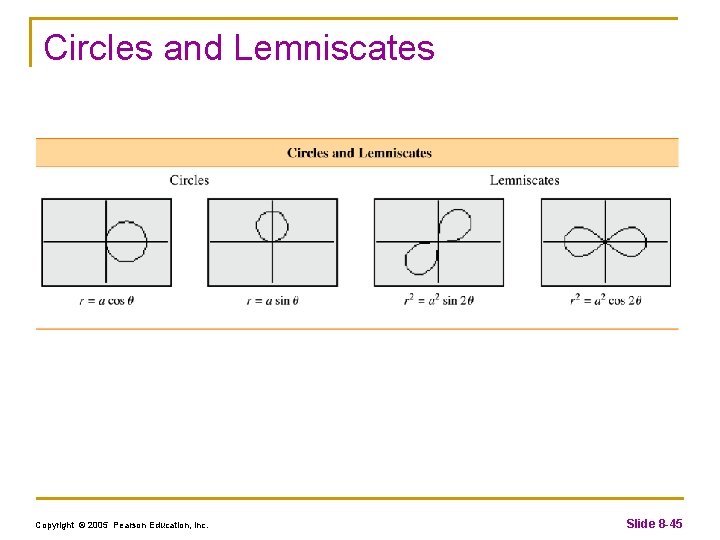
Circles and Lemniscates Copyright © 2005 Pearson Education, Inc. Slide 8 -45

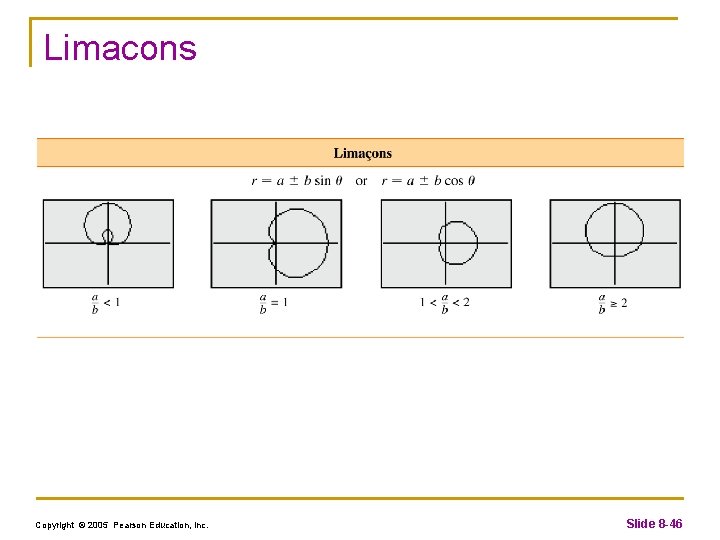
Limacons Copyright © 2005 Pearson Education, Inc. Slide 8 -46

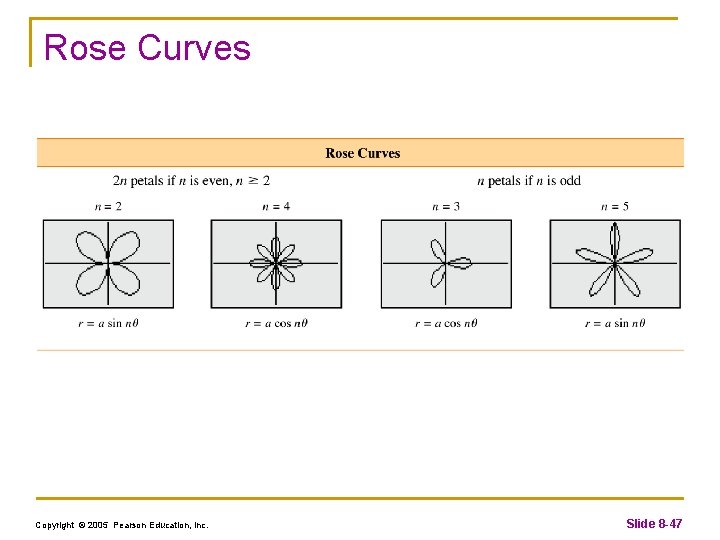
Rose Curves Copyright © 2005 Pearson Education, Inc. Slide 8 -47

8. 6 Parametric Equations, Graphs, and Applications Copyright © 2005 Pearson Education, Inc.

Parametric Equations of a Plane Curve n A plane curve is a set of points (x, y) such that x = f(t), y = g(t), and f and g are both defined on an interval I. The equations x = f(t) and y = g(t) are parametric equations with parameter t. Copyright © 2005 Pearson Education, Inc. Slide 8 -49

Graphing a Plane Curve Defined Parametrically Example: Let x = t 2 and y = 3 t - 1, for t in [ 3, 3]. Graph the set of ordered pairs (x, y). Solution: Make a table of corresponding values of t, x, and y over the domain of t. Copyright © 2005 Pearson Education, Inc. Slide 8 -50

Finding an Equivalent Rectangular Equation Example: Find a rectangular equation for the plane curve of the previous example defined as follows. x = t 2 , y = 3 t - 1, for t in [ 3, 3] Copyright © 2005 Pearson Education, Inc. Slide 8 -51

Graphing a Plane Curve Defined Parametrically Example: Graph the plane curve defined by x = 2 sin t, y = 3 cos t, for t in [0, 2 ]. Solution: Use the fact that sin 2 t + cos 2 t = 1. Square both sides of each equation; solve one for sin 2 t, the other for cos 2 t. Copyright © 2005 Pearson Education, Inc. Slide 8 -52

Finding Alternative Parametric Equation Forms Give two parametric representations for the equation of the parabola y = (x + 5)2 +3. Copyright © 2005 Pearson Education, Inc. Slide 8 -53

Application A small rocket is launched from a table that is 4 ft above the ground. Its initial velocity is 32 ft per sec, and it is launched at an angle of 60° with respect to the ground. Find the rectangular equation that models its path. What type of path does the rocket follow? How would you find the maximum height? Copyright © 2005 Pearson Education, Inc. Slide 8 -54