COP 4710 Databases Fall 2000 Todays Topic Chapter

COP 4710 Databases Fall, 2000 Today’s Topic Chapter 5: Improving the Quality of Relational Schemas David A. Gaitros September 18, 2000 Department of Computer Science Copyright by Dr. Greg Riccardi 1
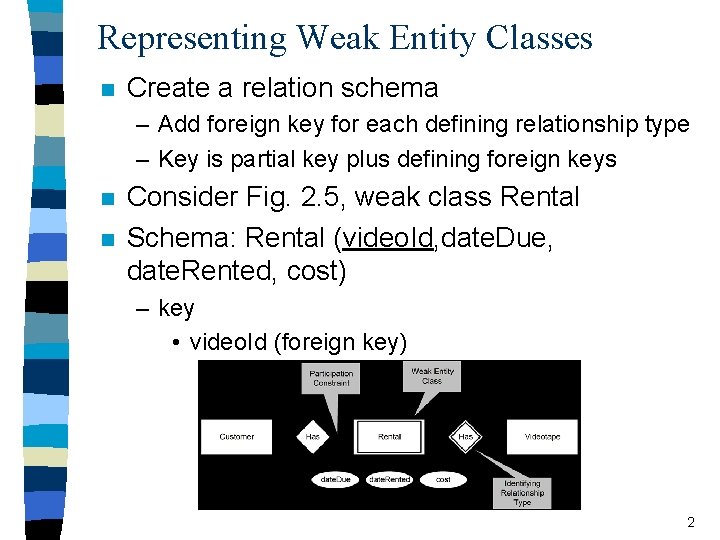
Representing Weak Entity Classes n Create a relation schema – Add foreign key for each defining relationship type – Key is partial key plus defining foreign keys n n Consider Fig. 2. 5, weak class Rental Schema: Rental (video. Id, date. Due, date. Rented, cost) – key • video. Id (foreign key) 2

Solving a 1 to Many Relationship Customer Table 1 M Video Inventory 3
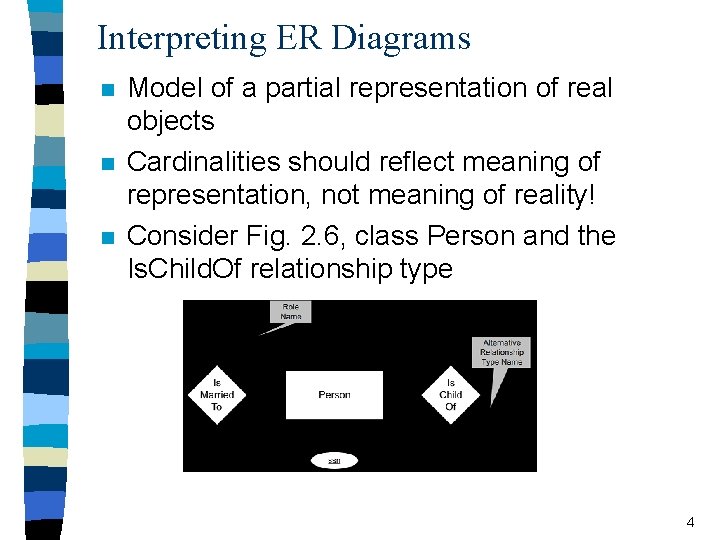
Interpreting ER Diagrams n n n Model of a partial representation of real objects Cardinalities should reflect meaning of representation, not meaning of reality! Consider Fig. 2. 6, class Person and the Is. Child. Of relationship type 4

Solving a 1 to Many Relationship Customer Table Children Match up Table 1 M Person Table The relationship with the spouse is taken care of in the person table with a single Column. Note the difference between the schema and table. 5

Functional Dependencies and Normalization n n Begin by discussing good and bad relation schemas Informal measures of the quality of relation schema design – – n Semantics of the attributes Reducing the redundant values in tuples Reducing the null values in tuples Disallowing spurious tuples Define Normal Forms as formal measures of the quality of schemas – restrictions on the form of relation schemas 6

Semantics of the Relation Attributes n n How to interpret the attribute values stored in a tuple? Guideline 1: Design a schema so that it is easy to explain its meaning. Keep attributes from different entities and relationships distinct. Example of mixing: – Owner. Car: (Oname, DLNum, Car. Id, Make, Manuf) – Oname is attribute of owner, Make is attribute of car! 7

Redundant Information in Tuples n Previous example of Owner. Car – Owner. Car: (Oname, DLNum, Car. Id, Make, Manuf) n Consider a table of Owner. Car : – (Joe, 123456789, 106, Plymouth, Chrysler) – (Moe, 223456789, 107, Plymouth, Chrysler) n n The Manuf attribute is redundant! This leads to difficulty in updates also called Update Anomalies – E. g. changing the Manuf for Joe requires also changing for Moe. 8

Update Anomalies n Insertion Anomalies – When inserting a new owner, we must correctly insert the Manuf field, or will create inconsistencies – Cannot create a car without an owner – Cannot create a make without a car and an owner n Deletion Anomalies – Deletion of owner of a car also deletes make and manufacturer of car – Deletion of owner of the last Plymouth deletes relationship between Plymouth and Chrysler n Modification Anomalies – Changing the make of a car requires consistency check – Cannot change so that a Plymouth is made by Ford n Guideline 2: no insertion, deletion, or modification anomalies allowed! 9

Null Values in Tuples n May have many attributes (fat relation) which do not apply to many tuples – Hence, many null values in many tuples – Takes lots of space – Not sure how to treat these in Sum, Count n Nulls can have many interpretations – Attribute does not apply – Attribute value is unknown – Value is known but absent n Guideline 3: Avoid placing attributes whose values may be null in a base relation. 10

First Normal Form (1 NF) n n 3 normal forms proposed by Codd in 1972 All attribute values are atomic (or indivisible). This rule is now part of the definition of relation. Hence, the translation from ERD to relational schema requires that multi-valued attributes be transformed into tables. See Step 6, p. 174. 11

Normal Forms based on Primary Keys n n Normalization includes testing and modifying a schema until it satisfies a set of rules Hope to ensure that update anomalies do not occur. Unsatisfactory schemes are decomposed by breaking up attributes in smaller relations. For each rule, if a particular relation violates the rule, that relation must be broken into smaller relations 12

Some definitions n n n superkey: a set of attributes of a relation whose values are unique within the relation. key, a superkey in which removal of any attribute makes it not a superkey. If there is more than one key, they are called candidate keys. primary key, arbitrarily designated candidate key, all other candidate keys are secondary keys. prime attribute, one which is a member of any key. nonprime attribute, one which is not prime. 13

Definition of Functional Dependency n A functional dependency is a constraint between 2 sets of attributes from the database – For each value of the first set there is a unique value of the second set n n X-->Y restricts the tuples that can be instances of R if t 1 and t 2 are instances of R – t 1(X) = t 2(X) then t 1(Y) = t 2(Y) n For example, – {DLNum} --> {Oname} – {Car. Id} --> {Make, Manuf} – {Make} --> {Manuf} n Candidate keys are left hand sides of functional dependencies 14

Second Normal Form (2 NF) n X-->Y is a full functional dependency if the removal of any attribute A from X removes the dependency – not X-{A} --> Y n X-->Y is a partial dependency if some attribute A may be removed without removing the dependency – X-{A} --> Y n A relation schema R is in 2 NF if every nonprime attribute is fully functionally dependent on the primary key of R 15

Consider the Car Registration Document n Fig. 5. 9 Sample car registration form 16

Example of Car Registration Schema n n This is a different car registration example from Fig. 5. 9 Relation owner – DLNum, Name, Address, City, State, Zip n Relation Car – Car. Id, DLNum, Make, Model, Manuf, Year, Color, Owner, Purch. Date, Tag. Num, Regis. Date n n R is set of all attributes of schema F is set of all functional dependencies – – – {DLNum} --> {Name, Address, City, State, Zip} {Car. Id} --> {Make, Model, Manuf, Year, Color} {Tag. Num} --> {Regis. Date} {Car. Id, DLNum} --> {Purch. Date, Tag. Num, . . . } and more! 17

Putting the Car. Reg Schema into 2 NF n Consider the Owner relation schema – {DLNum} is the primary key – Hence Owner is in 2 NF n Consider the Car relation schema – {Car. Id, DLNum} is primary key (multiple owners) – {Car. Id} --> {Make, Model, . . . } – Hence Car is not 2 NF n Create new relations – Car. Owner = {Car. Id, Owner, Purch. Date, Tag. Num, Regis. Date} – Car = {Car. Id, Make, Model, Manuf, Year, Color} n Is it 2 NF? 18

Rules for Functional Dependencies n Given a particular set of functional dependencies, we can find others using inference rules – Splitting/combining rules • A -> B 1 B 2 <=> A-> B 1 and A->B 2 – Trivial rules • A B -> B, for all A, B – Transitive rule • A -> B and B -> C => A B -> C n We are interested in the closure of the set of functional dependencies under these (and other) rules 19

Inference Rules for Functional Dependency n n n There are semantically obvious functional dependencies, usually specified by schema designer Other functional dependencies can be inferred from those Inference rules – – – Reflexive, X includes Y, X-->Y Augmentation, X-->Y then XZ-->YZ Transitive, X-->Y-->Z then X-->Z Decomposition, X-->YZ then X-->Y Union, X-->Y and X-->Z then X-->YZ Pseudotransitive, X-->Y and WY-->Z then WX-->Z 20

Definition of Key n A set of one or more attributes {A 1, . . . Ak} is a key for a relation R – Those attributes functionally determine all other attributes of R • no 2 distinct tuples can agree on the key – no proper subset of {A 1, . . . Ak} is a key of R • a key must be minimal n There can be more than one key in a relation – Department (Dept. Name, Dept. No, . . . ) • since both are unique, both are keys n A superkey (superset of a key) is a set of attributes that functionally determine all other attributes of the relation. 21

Third Normal Form (3 NF) n n Based on transitive dependency, or non-key dependency A functional dependency X-->Y is a transitive dependency if there is a set Z which is not a subset of any key, and for which X-->Z and Z->Y A relation schema is in 3 NF if there is no nonprime attribute which is functionally dependent on a non-key set of attributes. Example of {make}-->{manuf} violates 3 NF since make is not a key. 22

Transforming Car into 3 NF n n Car = {Car. Id, Make, Model, Manuf, Year, Color} {Car. Id}-->{Make, Model, Manuf, Year, Color} {Make} --> {Manuf} Not 3 NF Car = {Car. Id, Make, Model, Year, Color} Make. Manuf = {Make, Manuf} What about {Model}-->{Make}? 23

Boyce Codd Normal Form (BCNF) n n A relation R is BCNF iff for each non-trivial dependency {A 1, …Ak} -> B for R, – A 1…Ak is a superkey Alternatively, collect all similar violations – if A 1…Ak -> B 1…Bn then {A 1, …Ak} is a superkey A 3 NF relation is not BCNF only if there is – X -> A such that • X is not a superkey and • A is a prime attribute Any 2 -attribute relation is BCNF: e. g. R(a, b) – either a->b but not b->a, {a} is key but not {b} – a->b and b->a, both {a} and {b} are keys – neither a->b nor b->a, {a, b} is key 24

Why BCNF? n BCNF schemas do not exhibit anomalies – only redundancy is foreign key – each non-key attribute appears only once – only update and delete problems are • update of key attribute must be propagated to foreign keys • deletion of tuple must be propagated to foreign keys, either null or delete n All functional dependencies are key dependencies – Functional dependency constraints have been turned into key constraints – Database system can enforce key constraints 25

Conversion of DB Schema into BCNF n Consider a single relation schema – Identify a BCNF violation – Decompose the relation to remove the violation – Repeat until no violations occur n Repeat for every relation in the DB schema, including the new relations created by decomposition 26

Decomposition into BCNF n Suppose R has a BCNF violation – A 1…An -> B 1…Bm and {A 1, …An} is not superkey – Bs include all attributes that are dependent – let {C 1, …Ck} be all other attributes (not As or Bs) n Create 2 new relations – R 1(A 1, …An, B 1, …Bm} and R 2={A 1, …An, C 1, …Ck} – keys must be determined by considering resulting functional dependencies n Consider other examples in class 27

Second Normal Form (2 NF) n X-->Y is a full functional dependency if the removal of any attribute A from X removes the dependency – not X-{A} --> Y n X-->Y is a partial dependency if some attribute A may be removed without removing the dependency – X-{A} --> Y n A relation schema R is in 2 NF if every nonprime attribute is fully functionally dependent on every key of R 28

Consider the Car Registration Document n Fig. 5. 9 Sample car registration form 29

Inference Rules for Functional Dependency n n n There are semantically obvious functional dependencies, usually specified by schema designer Other functional dependencies can be inferred from those Inference rules – – – Reflexive, X includes Y, X-->Y Augmentation, X-->Y then XZ-->YZ Transitive, X-->Y-->Z then X-->Z Decomposition, X-->YZ then X-->Y Union, X-->Y and X-->Z then X-->YZ Pseudotransitive, X-->Y and WY-->Z then WX-->Z 30

Third Normal Form (3 NF) n n Based on transitive dependency, or non-key dependency A functional dependency X-->Y is a transitive dependency if there is a set Z which is not a subset of any key, and for which X-->Z and Z->Y A relation schema is in 3 NF if there is no nonprime attribute which is functionally dependent on a non-key set of attributes. Example of {make}-->{manuf} violates 3 NF since make is not a key. 31

Boyce Codd Normal Form (BCNF) n n A relation R is BCNF iff for each non-trivial dependency {A 1, …Ak} -> B for R, – A 1…Ak is a superkey Alternatively, collect all similar violations – if A 1…Ak -> B 1…Bn then {A 1, …Ak} is a superkey A 3 NF relation is not BCNF only if there is – X -> A such that • X is not a superkey and • A is a prime attribute Any 2 -attribute relation is BCNF: e. g. R(a, b) – either a->b but not b->a, {a} is key but not {b} – a->b and b->a, both {a} and {b} are keys – neither a->b nor b->a, {a, b} is key 32

Why BCNF? n BCNF schemas do not exhibit anomalies – only redundancy is foreign key – each non-key attribute appears only once – only update and delete problems are • update of key attribute must be propagated to foreign keys • deletion of tuple must be propagated to foreign keys, either null or delete n All functional dependencies are key dependencies – Functional dependency constraints have been turned into key constraints – Database system can enforce key constraints 33

Homework 4 n 1. What are the differences between an E-R model and a relational model of an information system? – No representation for relationships – Restrictions on domains – Specific representation as tables n 2. Why must keys be declared? Why is it not always possible to infer a key constraint from the contents of a table? – Key constraints are based on meaning, not on state – Example from Fig. 4. 1 n 3. Why is there no such thing as a weak relation schema? – Every schema has a superkey n 4. List the differences between attributes in an E-R diagram and attributes in the relational model. What restrictions are placed on attributes in the relational model? – Suggestions? 34

Homework 4, problem 5 n Translate the E-R diagram of Fig. 4. 4 into a database schema. – – Step 1: Entity class Customer to relation Customer Step 2: Add simple attributes to Customer Step 3: Add composite attributes to Customer Step 4: Weak entity class Other. User to relation Other. User – Step 5: Identifying relationship type to attribute – Step 6: Add other. User partial key as attribute and define key of relation Other. User 35

Homework 5 n 1. Give examples of three reasons why redundancy in schemas creates problems. – Different update anomalies n 2. Give an example (not from the book) of each type (deletion, insertion, modification) of anomaly for the schema and table of Fig. 5. 1. – Suggestions? n n 3. Is it necessary to declare functional dependencies, or is it possible to infer them from sample tables? Are there any apparent functional dependencies that can be inferred from the table of Fig. 5. 1 that are not functional dependencies? 36

Homework 5, problem 5 n 5. Suppose a student registration database has a table for student grades: – Grades: (student. Id, last. Name, first. Name, course. Id, course. Title, section. Number, semester, num. Hours, meeting. Time, meeting. Room, grade) n n n a. Give a sample table for the Grades schema that shows the rendundancy inherent in the meaning of the information. b. Define appropriate functional dependencies for the Grades schema. c. List all of the non-trivial dependencies that can be inferred from the dependencies of part b. c. Identify and remove any 2 NF violations in the Grades schema. Show the resulting schemas and tables. d. Identify and remove any 3 NF violations in the result of part c. Show the resulting schemas and tables. 37

Homework 5, problems 6 and 7 n 6. With no functional dependencies defined, what is the key of R? – {A, B, C, D, E, F, G, H} n n 7. Suppose {A, B} is the key of R and A -> {C, D} and B -> {E, F, H} a. List all of the non-trivial functional dependencies of R. – {A, B}->{C, D, E, F, G, H}, … n b. What dependencies represent 2 NF violations – {A}->{C, D}, {B}->{E, F, H} n c. Eliminate the 2 NF violations by decomposition – S 1: (A, B, G), S 2: (A, C, D), S 3: (B, E, F, H) n D. e. No 3 NF violations 38

Homework 5, problem 7, revised. n n Suppose {E} -> {F} d. What dependencies represent 3 NF violations – {E}->{F} n e. Eliminate the 3 NF violations – S 1: (A, B, G), S 2: (A, C, D), – S 4: (B, E, H), S 5: (E, F) n F. Suppose {E} -> {F, G} – Then {B} -> {E, F, G, H} – Hence, decomposition is different 39
- Slides: 39