COP 2500 Concepts in Computer Science Positional number

COP 2500 Concepts in Computer Science Positional number systems 1. - Decimal number system 2. - Binary number system 3. - Hexadecimal number system 4. - Base conversions

COP 2500 Concepts in Computer Science Positional number systems When we need to write the number three hundred and twenty five using decimal digits we use the following sequence of digits: 325 What do we know about this number? It is written using decimal digits (a digit from 0 to 9 in decimal notation), which means that the base of the decimal number system is 10 (the decimal system has ten symbols or digits). Formally we can write 325 as: 3 x 102 + 2 x 101 + 5 x 100 = (3 x 100) + (2 x 10) + (5 x 1) = 300 + 20 + 5 = 325 Note that 100 = 1

COP 2500 Concepts in Computer Science Positional number systems Formally we can write 325 as: 3 x 102 + 2 x 101 + 5 x 100 = (3 x 100) + (2 x 10) + (5 x 1) = 300 + 20 + 5 = 325 Note that 100 = 1 By denoting the base of the system as b = 10, we can rewrite 325 as: 325 = 3 x b 2 + 2 x b 1 + 5 x b 0 For any number we will refer to each digit by “di”, where “d” represents the digit and “i” indicates the position in the sequence. Thus we have that any number can be represented by a sequence of digits: dn dn-1. . . d 2 d 1 d 0 In our example, d 2 = 3, d 1 = 2, and d 0 = 5

COP 2500 Concepts in Computer Science Positional number systems Therefore any number can be represented by a sequence of digits: dn. . . d 2 d 1 d 0 And its value can be computed as follows: dn. . . d 2 d 1 d 0 = d n x b n. . . d 2 x b 2 + d 1 x b 1 + d 0 x b 0 Example: d 3 d 2 d 1 d 0 4 7 6 2

COP 2500 Concepts in Computer Science Positional number systems Binary numbers can be represented in the same way: ( d n. . . d 2 d 1 d 0 )2 Indicates that the base (b) is binary And its value can be computed similarly but in this case the base b = 2. dn. . . d 2 d 1 d 0 = d n x b n. . . d 2 x b 2 + d 1 x b 1 + d 0 x b 0 Example: (10101)2 = 1 x 24 + 0 x 23 + 1 x 22 + 0 x 21 + 1 x 20 1 x 16 + 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1 16 + 0 + 4 + 0 + 1 = (21) 10

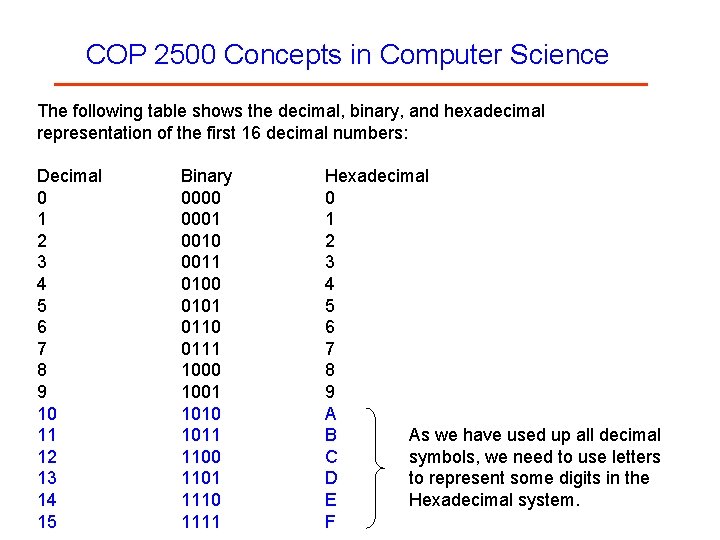
COP 2500 Concepts in Computer Science The following table shows the decimal, binary, and hexadecimal representation of the first 16 decimal numbers: Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Binary 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 Hexadecimal 0 1 2 3 4 5 6 7 8 9 A As we have used up all decimal B symbols, we need to use letters C to represent some digits in the D Hexadecimal system. E F

COP 2500 Concepts in Computer Science From hexadecimal to binary As each hexadecimal number can be represented by four binary digits, then to convert an hexadecimal number to binary we proceed as follows: (7 AF 3)16 = ( ? )2 Starting from left to right each hexadecimal digit is replaced by its binary representation: 7 = 0111 A = 1010 F = 1111 0111 1010 1111 0011 Note: see the table in the previous slide. 3 = 0011

COP 2500 Concepts in Computer Science From binary to hexadecimal We need to convert the following binary number to hexadecimal: (1011111000)2 = ( ? )16 Starting from right to left we make groups of four bits. If the last group on the right has less than four bits we add some padding zeros. 1011111000 0010 1111 1000 2 FB 8

COP 2500 Concepts in Computer Science Convert from decimal to binary: for example, (147)10 = ( ? )2 2 |147 2|73 2|36 2|18 2|9 2|4 2|2 2|1 0 1 1 0 0 1 Read from bottom to top the number is: (10010011)2

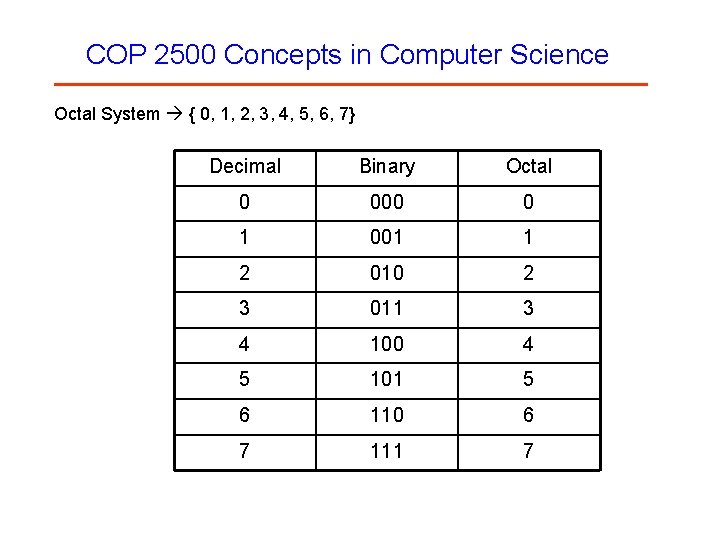
COP 2500 Concepts in Computer Science Octal System { 0, 1, 2, 3, 4, 5, 6, 7} Decimal Binary Octal 0 000 0 1 001 1 2 010 2 3 011 3 4 100 4 5 101 5 6 110 6 7 111 7

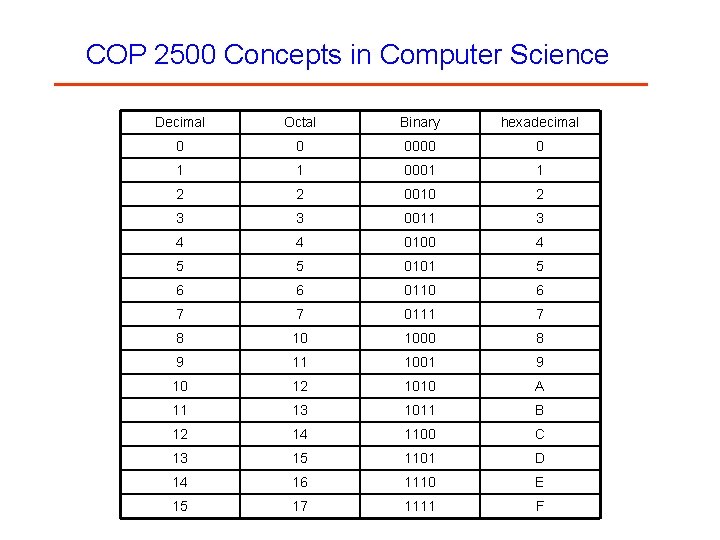
COP 2500 Concepts in Computer Science Decimal Octal Binary hexadecimal 0 0 0000 0 1 1 0001 1 2 2 0010 2 3 3 0011 3 4 4 0100 4 5 5 0101 5 6 6 0110 6 7 7 0111 7 8 10 1000 8 9 11 1001 9 10 12 1010 A 11 13 1011 B 12 14 1100 C 13 15 1101 D 14 16 1110 E 15 17 1111 F

COP 2500 Concepts in Computer Science The End