COORDINATE SYSTEMS TRANSFORMATION 1 6 CARTESIAN COORDINATES 1

COORDINATE SYSTEMS & TRANSFORMATION 1. 6 CARTESIAN COORDINATES 1. 7 CIRCULAR CYLINDRICAL COORDINATES 1. 8 SPHERICAL COORDINATES 1. 9 TRANSFORMATION BETWEEN COORDINATE SYSTEMS

1. 6 CARTESIAN COORDINATES • Consists of three mutually orthogonal axes and a point in space is denoted as

CARTESIAN COORDINATES (Cont’d) • The location of the point is defined by the intersection of three planes. • Example of location of points and

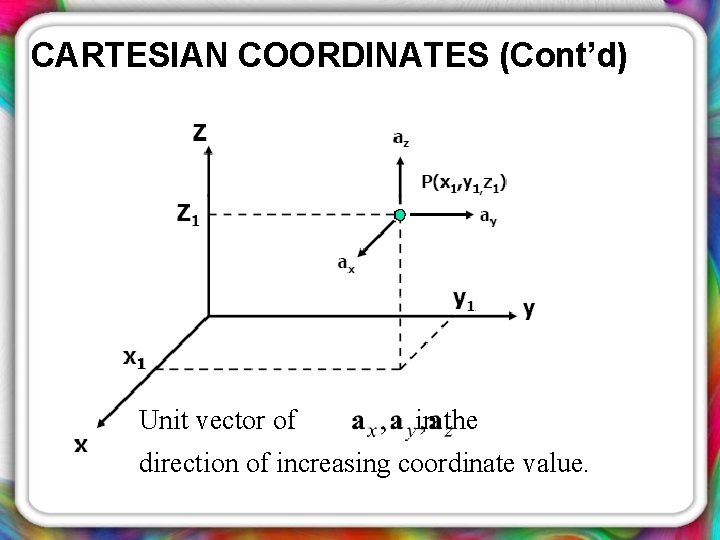
CARTESIAN COORDINATES (Cont’d) Unit vector of in the direction of increasing coordinate value.

CARTESIAN COORDINATES (Cont’d) • From previous point P, increase each coordinate value by a differential amount and obtain three slightly displaced planes intersecting at point P’, whose coordinates are , and

CARTESIAN COORDINATES (Cont’d) • The six planes define a rectangular parallelepiped whose: Ø Volume: Ø Surface with differential area: Ø Increment in length:

CARTESIAN COORDINATES (Cont’d) Differential surfaces:

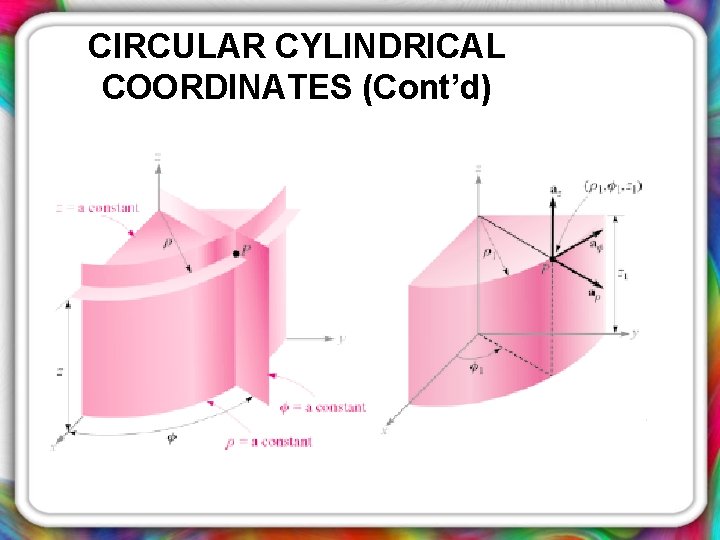
1. 7 CIRCULAR CYLINDRICAL COORDINATES • Form by three surfaces or planes: Ø Plane of z (constant value of z) Ø Cylinder centered on the z axis with radius of Plane perpendicular to x-y plane and rotate about the z axis by angle of Ø • Unit vector of in the direction of increasing coordinate value.

CIRCULAR CYLINDRICAL COORDINATES (Cont’d)

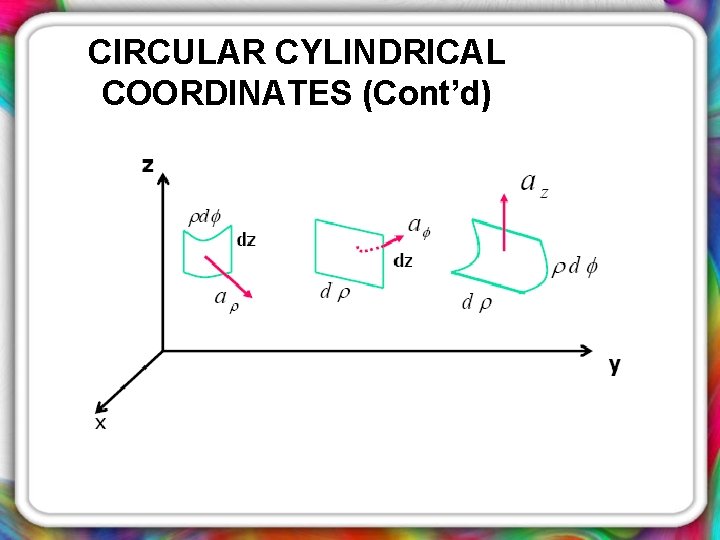
CIRCULAR CYLINDRICAL COORDINATES (Cont’d) • By increasing each coordinate value with a differential increment , it produces a shape of truncated wedge.

CIRCULAR CYLINDRICAL COORDINATES (Cont’d) • The truncated wedge whose: Ø Volume: Ø Surface with differential area: Ø Increment in length:

CIRCULAR CYLINDRICAL COORDINATES (Cont’d) Remember ? ! Increment in length for direction: is not increment in length!

CIRCULAR CYLINDRICAL COORDINATES (Cont’d) Differential surfaces:

CIRCULAR CYLINDRICAL COORDINATES (Cont’d)

CIRCULAR CYLINDRICAL COORDINATES (Cont’d) • The variables of Cartesian and cylindrical coordinate systems are easily related to each other.

EXAMPLE 5 A cylinder with radius of Determine: and length of (i) The volume enclosed. (ii) The surface area of that volume. .

SOLUTION TO EXAMPLE 5 (i) For volume enclosed, we integrate:

SOLUTION TO EXAMPLE 5 (Cont’d) (ii) For surface area of the volume:

EXAMPLE 6 The surfaces define a closed surface. Find: (a) The enclosed volume. (b) The total area of the enclosing surface. (a) The length of the longest straight (b) line that lies entirely within the (c) volume.

SOLUTION TO EXAMPLE 6 (a) The enclosed volume: The limits on the integration must be converted to radians!!

SOLUTION TO EXAMPLE 6 (Cont’d) (b) The total area of the enclosed surface:

SOLUTION TO EXAMPLE 6 (Cont’d) (c) Performing these points to Cartesian coordinates, these become: Taking A and B as vectors directed from the origin, the requested length is:

1. 8 SPHERICAL COORDINATES • Point P in spherical coordinate can be denoted as. Ø distance from origin angle between the z axis and the line from origin to point P Ø angle between x axis and projection in z=0 plane Ø

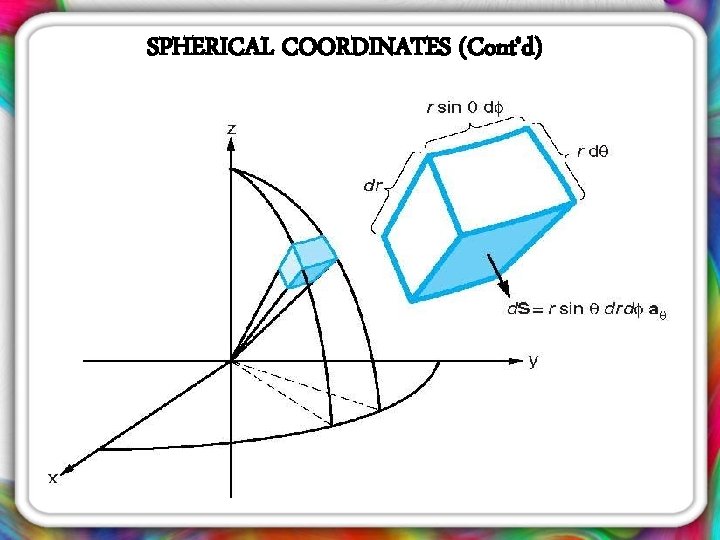
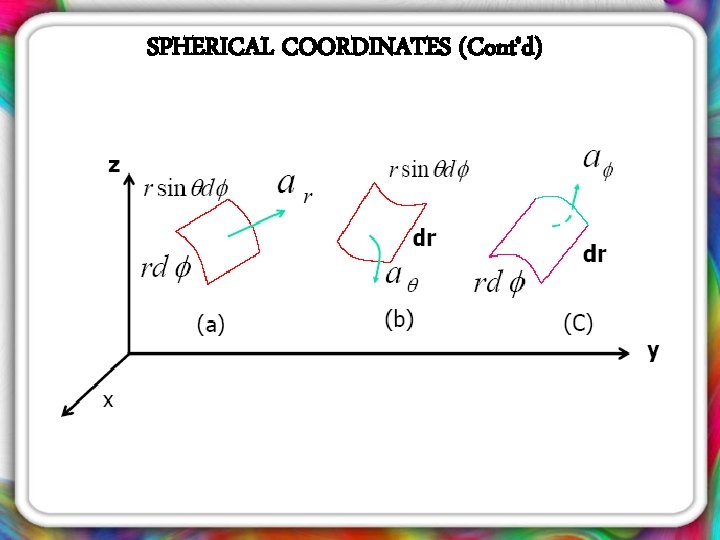
SPHERICAL COORDINATES (Cont’d) • By increasing each coordinate value with a differential increment , a differential volume can be constructed.

SPHERICAL COORDINATES (Cont’d)

SPHERICAL COORDINATES (Cont’d) • However, the increment of length is different from the differential increment previously, where: Ø distance between two radius Ø distance between two angles Ø distance between two radial planes at angles

SPHERICAL COORDINATES (Cont’d) • It has: Ø Volume: Ø Surface with differential area: Ø Increment in length:

SPHERICAL COORDINATES (Cont’d) Differential surfaces:

SPHERICAL COORDINATES (Cont’d)

SPHERICAL COORDINATES (Cont’d) • The variables of Cartesian and spherical coordinate systems are easily related to each other.

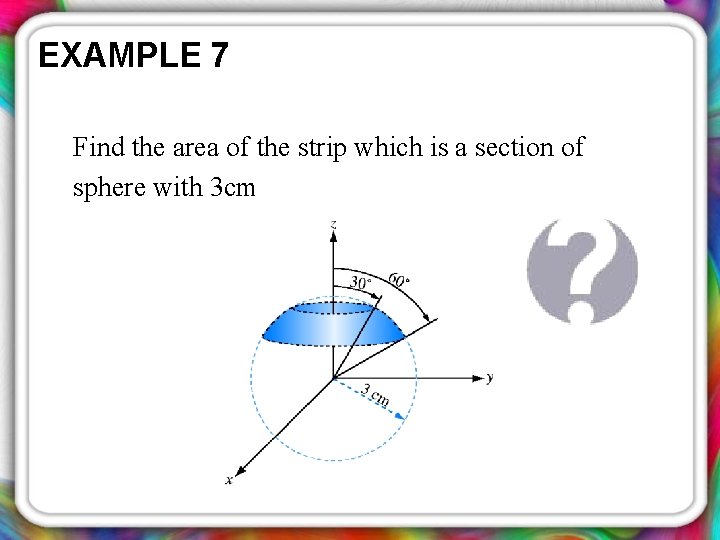
EXAMPLE 7 Find the area of the strip which is a section of sphere with 3 cm

SOLUTION TO EXAMPLE 7 Use differential surface with constant radius R, which is in direction.

VERY IMPORTANT!! Cartesian Cylindrical Spherical Differential in length Differential Surface Differential Volume

1. 9 TRANSFORMATION • Transformation of Cartesian, cylindrical and spherical coordinate are obtain geometrically. (i) Transformation between Cartesian and cylindrical:

TRANSFORMATION (Cont’d) (ii) Transformation between Cartesian and spherical:

EXAMPLE 8 Let (Circular cylindrical vector) be converted to (Cartesian vector).

SOLUTION TO EXAMPLE 8 For Cartesian vector: Let Cartesian vector component, So,

SOLUTION TO EXAMPLE 8 (Cont’d) From figure, WHY ? ! So,

SOLUTION TO EXAMPLE 8 (Cont’d) For: And,

SOLUTION TO EXAMPLE 8 (Cont’d) Finally, Vector for Cartesian coordinate Put into matrix form:

IMPORTANT!! From previous example, we can conclude that the transformation emphasizing on the dot product, where:

EXAMPLE 9 Given in Cartesian coordinates, Evaluate: (i) Point P in Cylindrical coordinates (ii)Vector at P in Cartesian coordinates system (iii)Vector in Cylindrical coordinates system (iv)Vector at P in Cylindrical coordinates system

SOLUTION TO EXAMPLE 9 (i) In Cartesian coordinates, point P Transformation for point P:

SOLUTION TO EXAMPLE 9 (Cont’d) (ii) Vector at P in Cartesian coordinates systems is easily obtained as: (iii) Vector in Cylindrical coordinates systems

SOLUTION TO EXAMPLE 9 (Cont’d) Where,

SOLUTION TO EXAMPLE 9 (Cont’d) But So, Vector in Cylindrical coordinates systems

SOLUTION TO EXAMPLE 9 (Cont’d) (iv) For vector at P in Cylindrical coordinates system, plug in the values of coordinate P in Cylindrical coordinate into vector below:

SOLUTION TO EXAMPLE 9 (Cont’d) Therefore,