Coordinate Systems conventional Cartesian reference system Y Z

Coordinate Systems (conventional Cartesian reference system) Y Z X Z Y X

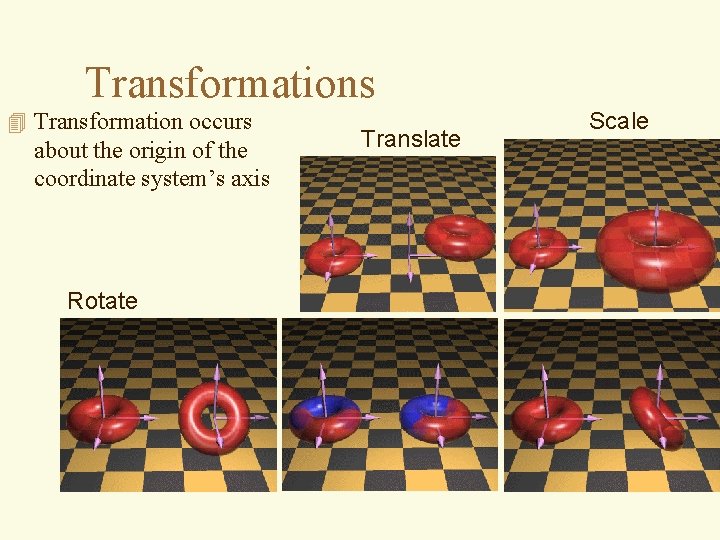
Transformations 4 Transformation occurs about the origin of the coordinate system’s axis Rotate Translate Scale

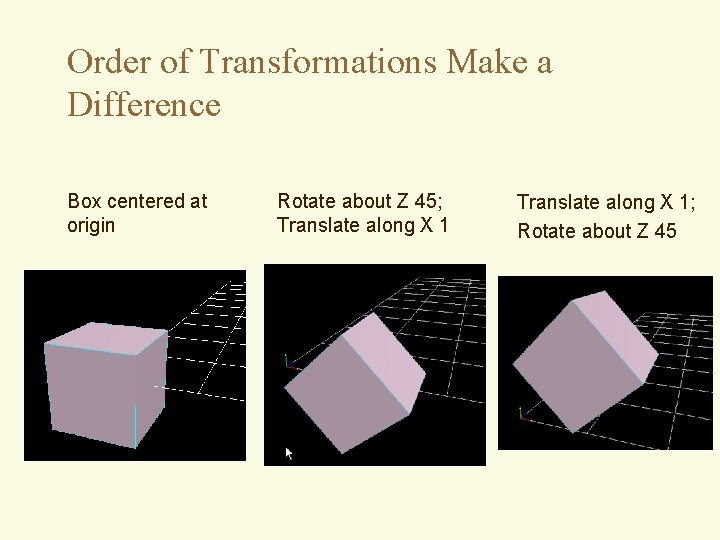
Order of Transformations Make a Difference Box centered at origin Rotate about Z 45; Translate along X 1; Rotate about Z 45

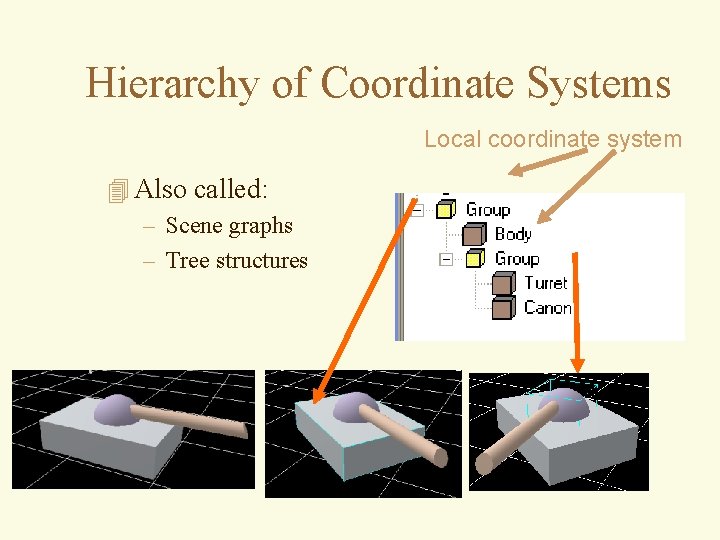
Hierarchy of Coordinate Systems Local coordinate system 4 Also called: – Scene graphs – Tree structures

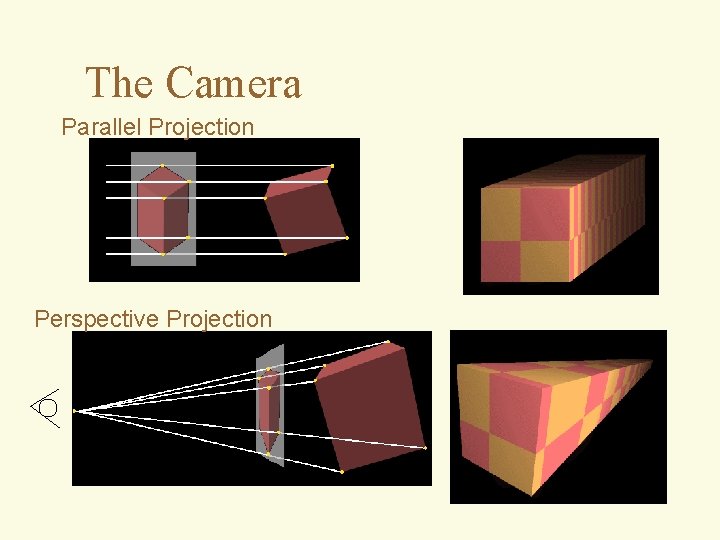
The Camera Parallel Projection Perspective Projection

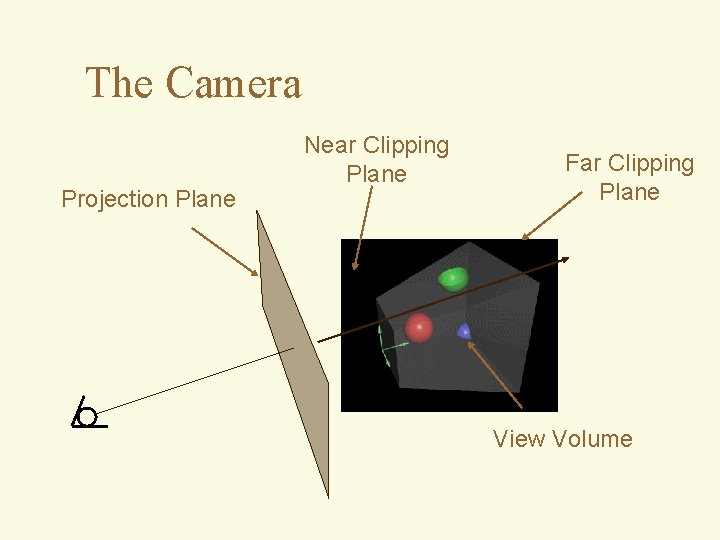
The Camera Projection Plane Near Clipping Plane Far Clipping Plane View Volume

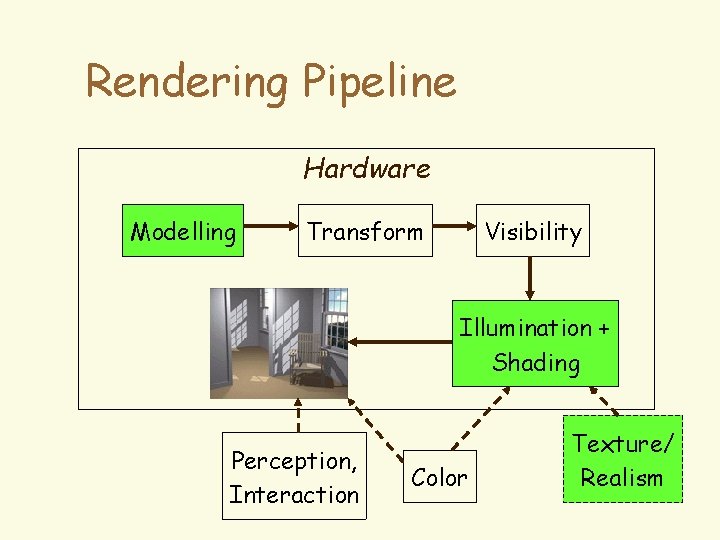
Rendering Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Interaction Color Texture/ Realism

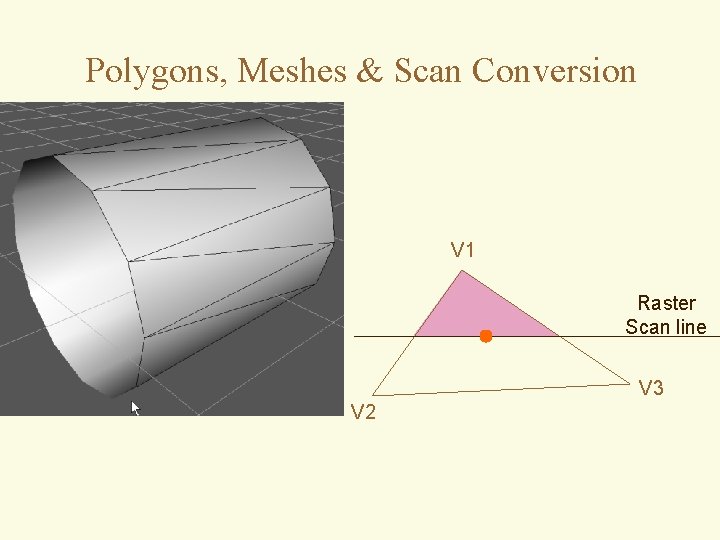
Polygons, Meshes & Scan Conversion V 1 Raster Scan line V 3 V 2

Approximating Curved Surfaces with Flat Polygons Flat Shading – each polygon face has a normal that is used to perform lighting calculations.

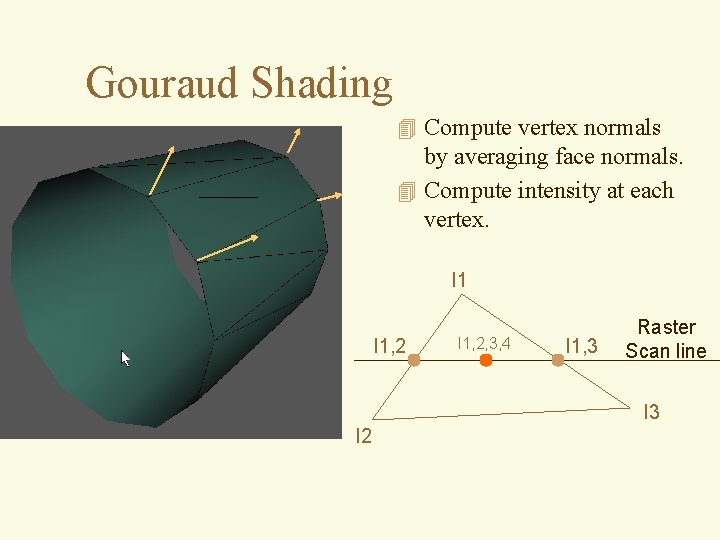
Gouraud Shading 4 Compute vertex normals by averaging face normals. 4 Compute intensity at each vertex. I 1, 2, 3, 4 I 1, 3 Raster Scan line I 3 I 2

Illumination / Shading 4 Distinction between illumination and shading models – illumination - calculate intensity at a point on surface – shading - uses calculated intensities to shade polygons (uses illumination models) 4 we’ll review the important models

Illumination / Shading 4 We’ll talk more about concepts that lead to realism: – global illumination: • ray tracing + radiosity – “special effects/tricks”: • shadows, texture maps, bump maps, antialiasing, transparency, reflection maps, refraction

Local Illumination 4 Local vs. global illumination models – local (typically) - how is one point of the scene illuminated directly by the light source • is light source only source of illumination? • Simple models lump the rest into a single ambient term • do not account for reflections within the environment

Local Illumination 4 Local vs. global illumination models – global - illuminates the whole scene • typically makes use of local illumination model • incorporates inter-reflectance of objects

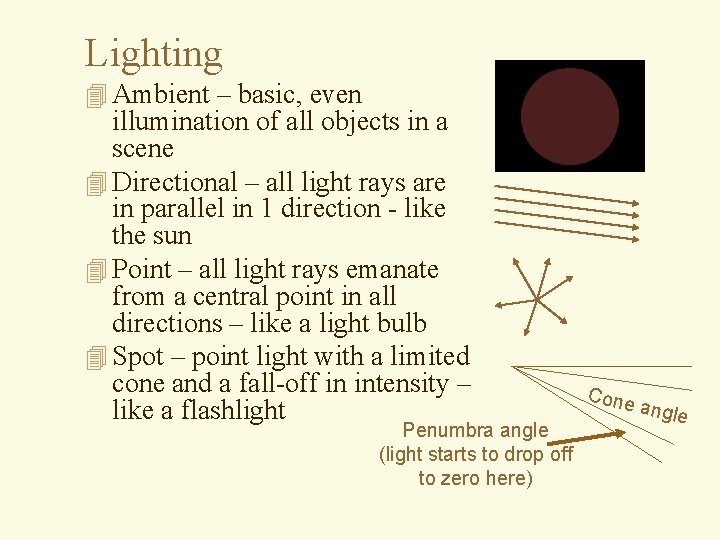
Lighting 4 Ambient – basic, even illumination of all objects in a scene 4 Directional – all light rays are in parallel in 1 direction - like the sun 4 Point – all light rays emanate from a central point in all directions – like a light bulb 4 Spot – point light with a limited cone and a fall-off in intensity – like a flashlight Penumbra angle (light starts to drop off to zero here) Cone a ngle

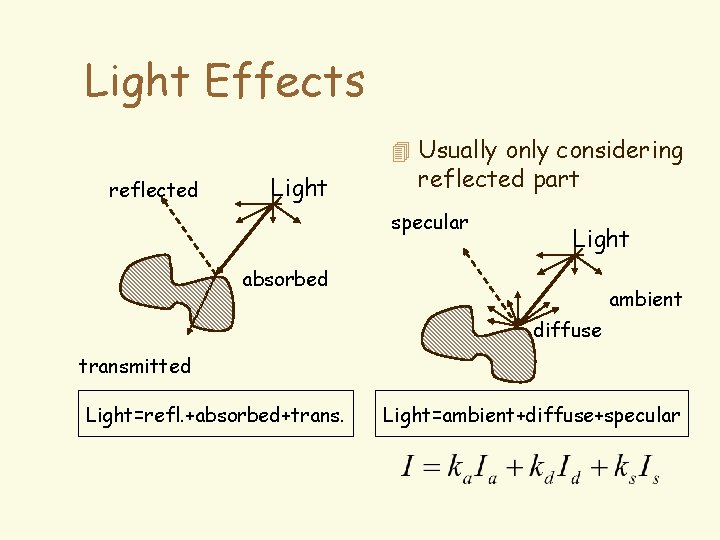
Light Effects 4 Usually only considering reflected Light reflected part specular Light absorbed ambient diffuse transmitted Light=refl. +absorbed+trans. Light=ambient+diffuse+specular

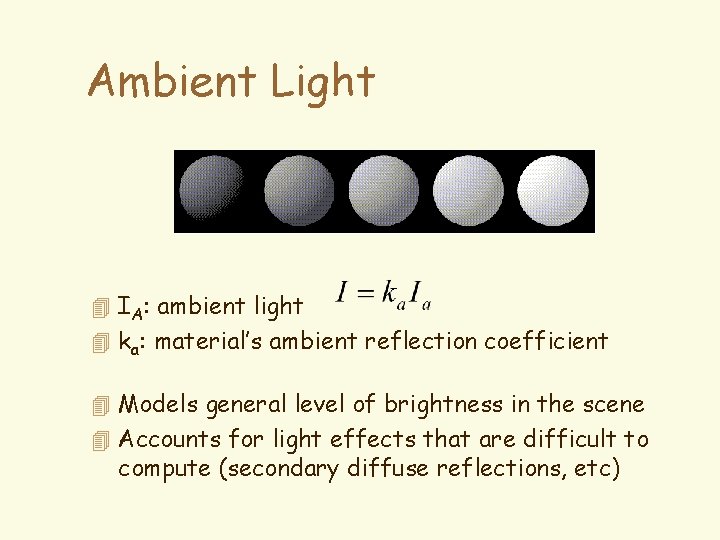
Ambient Light 4 is the light in the environment evenly reaching all surfaces from all directions 4 light location doesn’t matter 4 eye position doesn’t matter 4 IA: ambient light 4 ka: material’s ambient reflection coefficient

Ambient Light 4 IA: ambient light 4 ka: material’s ambient reflection coefficient 4 Models general level of brightness in the scene 4 Accounts for light effects that are difficult to compute (secondary diffuse reflections, etc)

Ambient Light Example

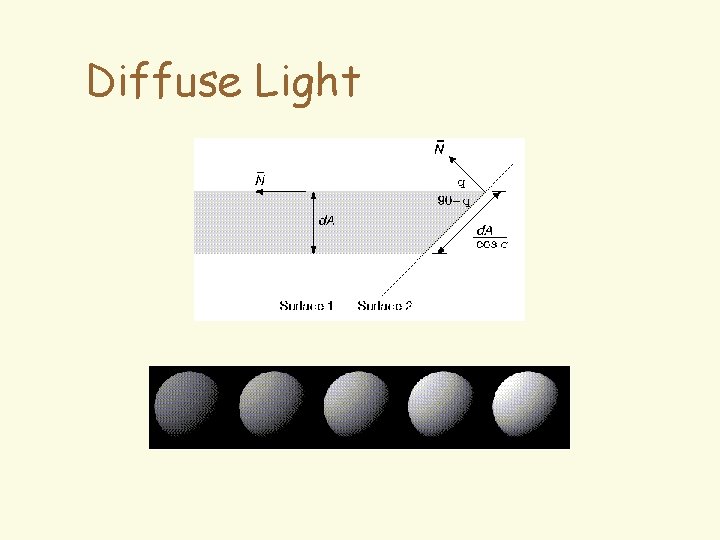
Diffuse Light 4 Light absorbed by the surface and then reflected equally to all directions 4 Models dullness, roughness of a surface Lambert’s Law: (perfectly diffuse surface) 4 Id: intensity of light source Light N f 4 kd: material’s diffuse reflection coefficient 4 N: normal vector (normalized) 4 L: light source vector (normalized) L

Diffuse Light

Diffuse Lighting Example

Specular Light 4 Light that is reflected from the surface unequally to all directions 4 Models reflections on shiny surfaces Phong’s Law: Eye R a R R R n=inf. n=large n=small N ff Light L

Specular light example

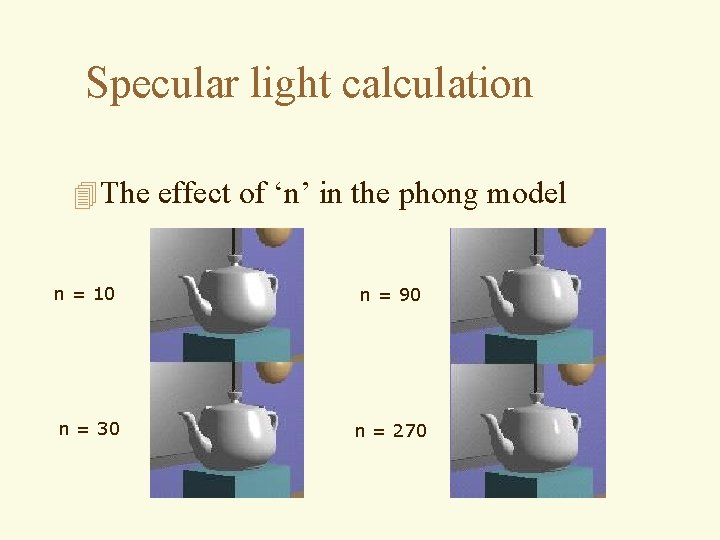
Specular light calculation 4 The effect of ‘n’ in the phong model n = 10 n = 90 n = 30 n = 270

Depth Cueing/Illumination 4 Theory - illumination fall-off with square of 4 4 4 distance 1/d 2 doesn’t give good results often a factor of 1/d or 1/(d+c) is used a way to simulate fog - linear fade … use start s and e fade distances d = distance from viewer:

Depth Cueing/Illumination

Shading a Polygon 4 Illumination Model: determine the color of a 4 4 surface (data) point by simulating some light attributes. Local IM: deals only with isolated surface (data) point and direct light sources. Global IM: takes into account the relationships between all surfaces (points) in the environment. Shading Model: applies the illumination models at a set of points and colors the whole scene. Texture Mapping: remappes and avgs. any value above (diffuse) from a 2 d picture or map

Shading Polyhedra 4 Flat (facet) shading: – Works well for objects really made of flat faces. – Appearance depends on number of polygons for curved surface objects. 4 If polyhedral model is an approximation then need to smooth.

Interpolated shading. 4 Wylie, Romney, Evans and Erdahl pioneered linear interpolation of shading information from the vertices. 4 Gouraud generalized this to arbitrary polygons. 4 Interpolate illumination in same manner as we interpolated z for z-buffering. – Not physically correct for illumination. 4 Assumption of polygon approximating a curved surface gives rise to largest error.

Gouraud shading

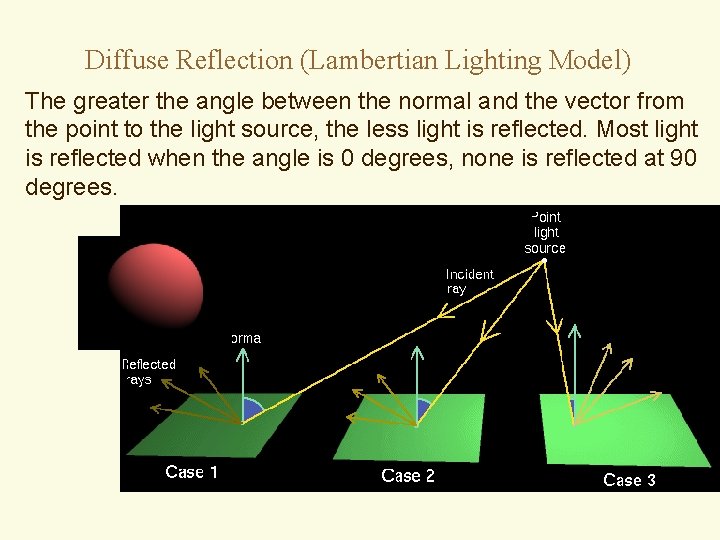
Diffuse Reflection (Lambertian Lighting Model) The greater the angle between the normal and the vector from the point to the light source, the less light is reflected. Most light is reflected when the angle is 0 degrees, none is reflected at 90 degrees.

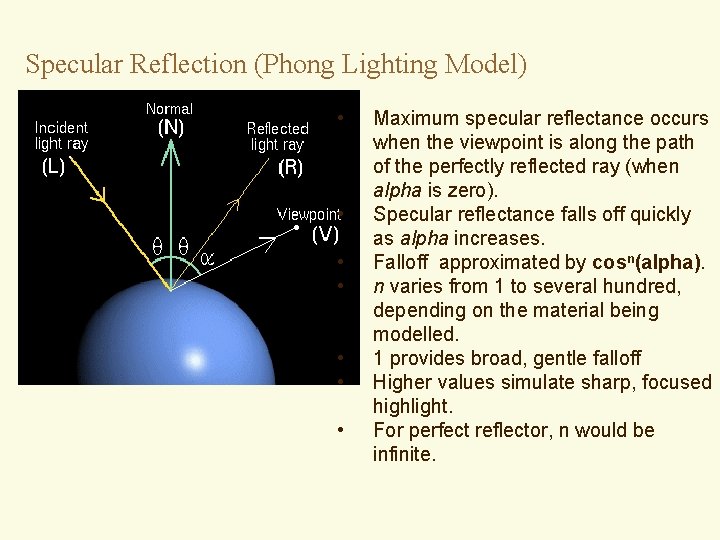
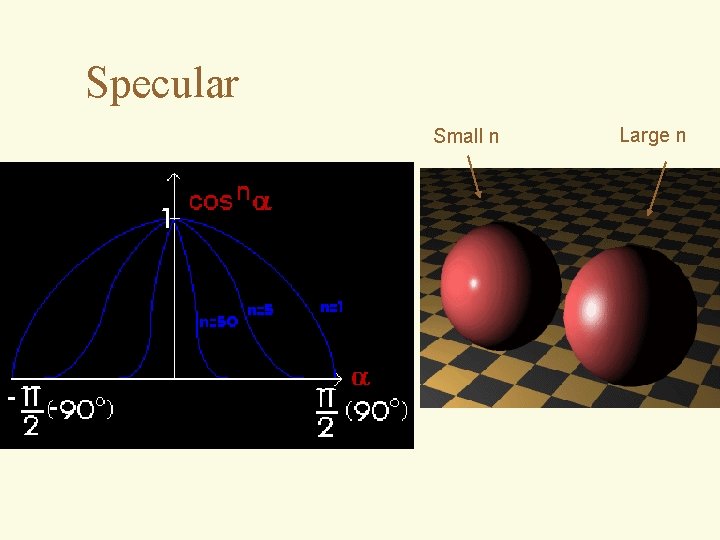
Specular Reflection (Phong Lighting Model) • • Maximum specular reflectance occurs when the viewpoint is along the path of the perfectly reflected ray (when alpha is zero). Specular reflectance falls off quickly as alpha increases. Falloff approximated by cosn(alpha). n varies from 1 to several hundred, depending on the material being modelled. 1 provides broad, gentle falloff Higher values simulate sharp, focused highlight. For perfect reflector, n would be infinite.

Specular Small n Large n

Shading - efficiently 4 Constant Shading: 4 compute illumination at one point of the primitive 4 4 (e. g. surface) and apply it for the whole primitive. Interpolated Shading: compute illumination at borders (e. g. vertices) of the primitive and interpolate the color Accurate Shading: compute illumination at every point of the primitive I 3 I 1 I 2

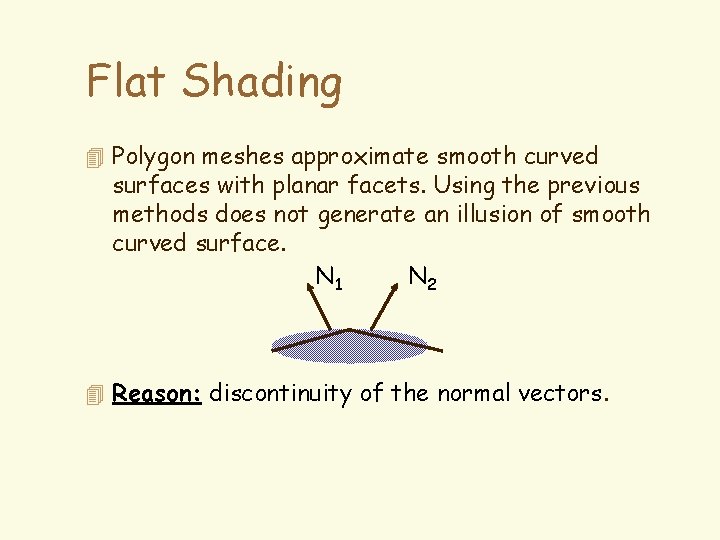
Flat Shading 4 Polygon meshes approximate smooth curved surfaces with planar facets. Using the previous methods does not generate an illusion of smooth curved surface. N 1 N 2 4 Reason: discontinuity of the normal vectors.

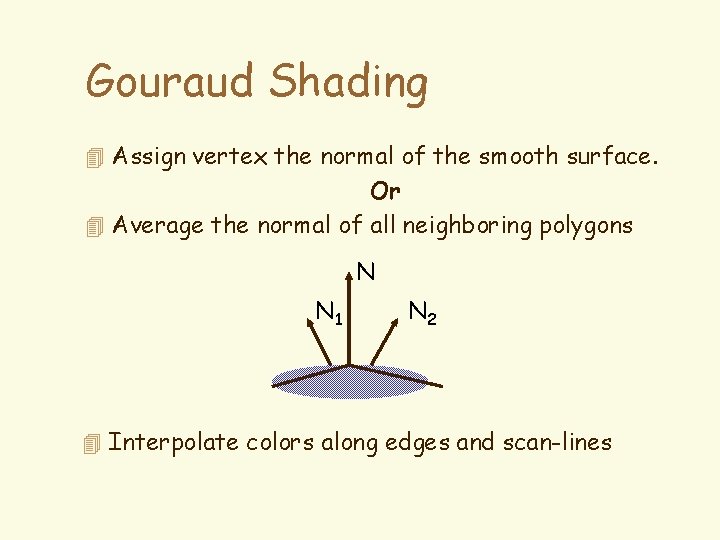
Gouraud Shading 4 Assign vertex the normal of the smooth surface. Or 4 Average the normal of all neighboring polygons N N 1 N 2 4 Interpolate colors along edges and scan-lines

Gouraud Shading Flat Shading Gouraud Shading

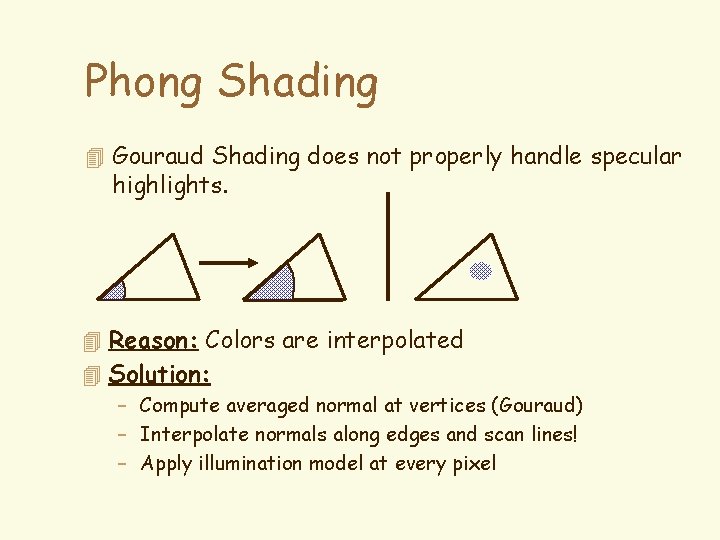
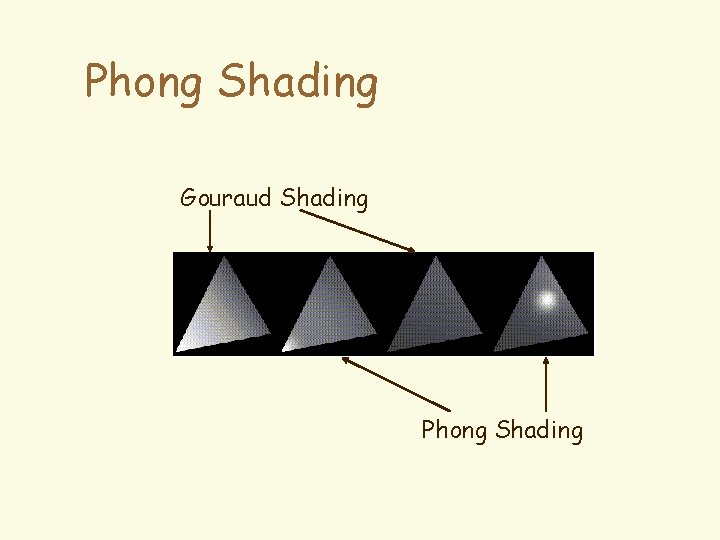
Phong Shading 4 Gouraud Shading does not properly handle specular highlights. 4 Reason: Colors are interpolated 4 Solution: – Compute averaged normal at vertices (Gouraud) – Interpolate normals along edges and scan lines! – Apply illumination model at every pixel

Phong Shading Gouraud Shading Phong Shading

Textures 4 Describe color variation in interior of 3 D polygon – When scan converting a polygon, vary pixel colors according to values fetched from a texture Texture Surface Image Angel Figure 9. 3

Surface Textures 4 Add visual detail to surfaces of 3 D objects With surface texture Polygonal model

Surface Textures 4 Add visual detail to surfaces of 3 D objects

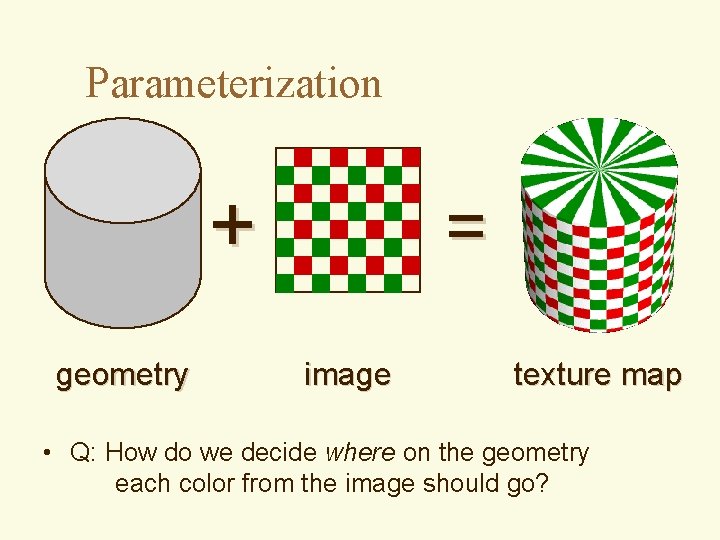
Parameterization + geometry = image texture map • Q: How do we decide where on the geometry each color from the image should go?

Option: Varieties of projections

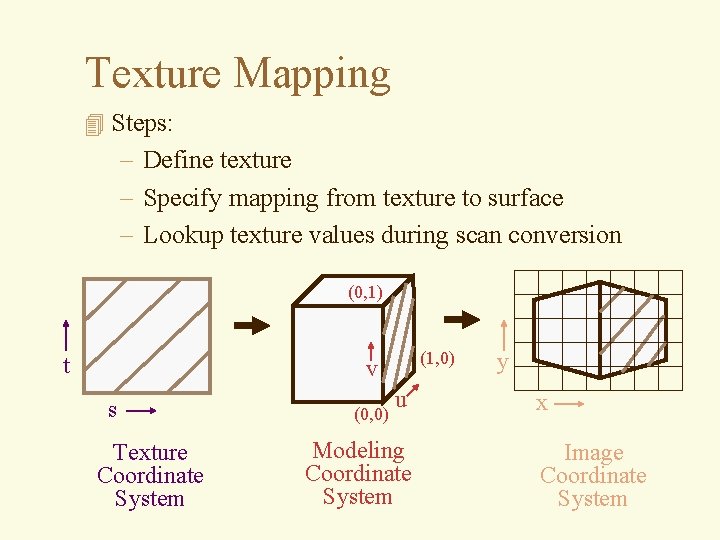
Texture Mapping 4 Steps: – Define texture – Specify mapping from texture to surface – Lookup texture values during scan conversion (0, 1) t (1, 0) v s Texture Coordinate System (0, 0) u Modeling Coordinate System y x Image Coordinate System

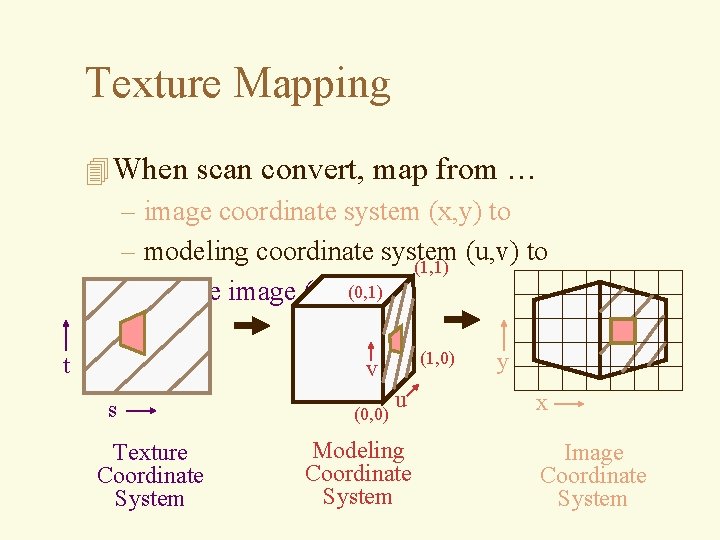
Texture Mapping 4 When scan convert, map from … – image coordinate system (x, y) to – modeling coordinate system (u, v) to (1, 1) – texture image (t, s)(0, 1) t (1, 0) v s Texture Coordinate System (0, 0) u Modeling Coordinate System y x Image Coordinate System

Texture Mapping 4 Scan conversion – Interpolate texture coordinates down/across scan lines – Distortion due to bilinear interpolation approximation

Texture Filtering 4 Aliasing is a problem Point sampling Area filtering Angel Figure 9. 5

Texture Filtering 4 Size of filter depends on projective warp – Can prefiltering images Magnification Minification Angel Figure 9. 14

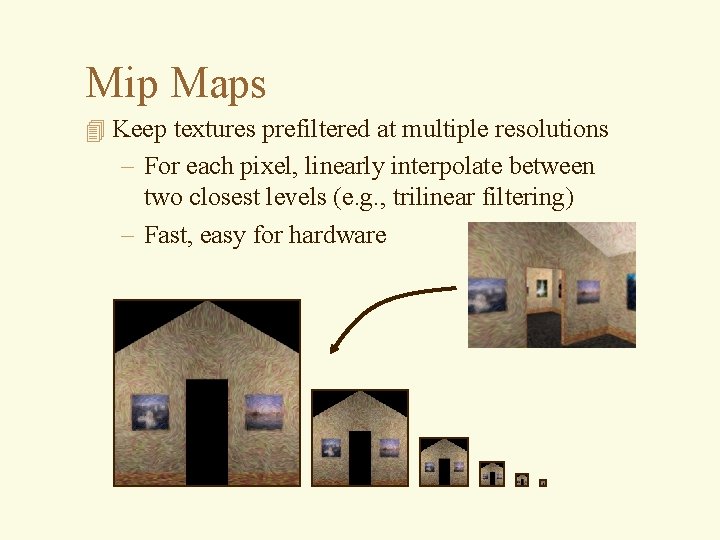
Mip Maps 4 Keep textures prefiltered at multiple resolutions – For each pixel, linearly interpolate between two closest levels (e. g. , trilinear filtering) – Fast, easy for hardware

What is a Texture? 4 MAP surface detail from a predefined (easy table (“texture”) to a simple polygon 4 Color 4 specular ‘color’ (environment map) 4 normal vector perturbation (bump 4 map) 4 displacement mapping 4 transparency 4. . .

Bump Mapping 4 Modifies the direction of the surface normal.

Texture and Bump Mapping 4 Diffuse and normal remapping

Displacement Mapping 4 Modifies the surface position in the direction of the surface normal.