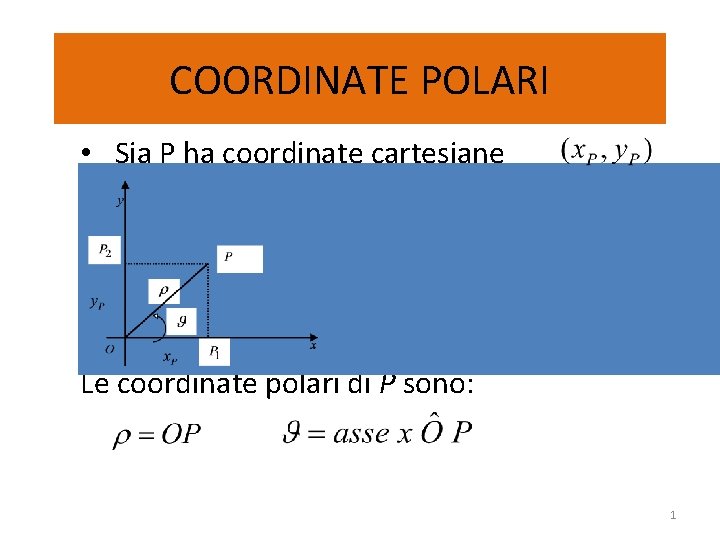
COORDINATE POLARI Sia P ha coordinate cartesiane Le

COORDINATE POLARI • Sia P ha coordinate cartesiane Le coordinate polari di P sono: 1

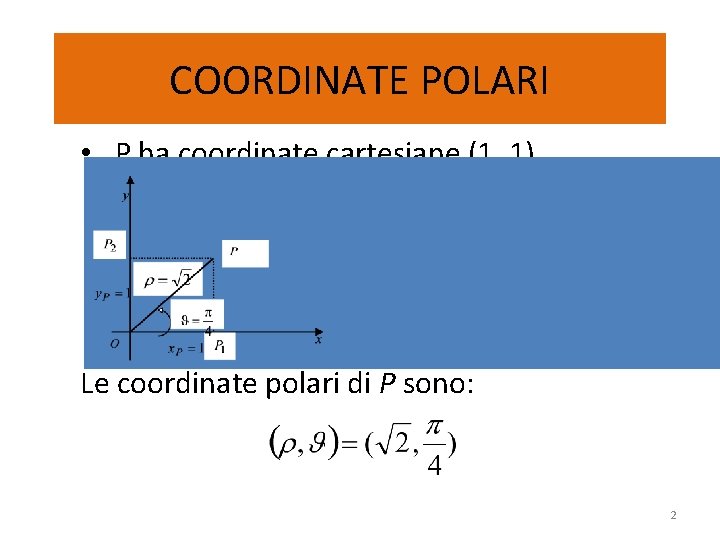
COORDINATE POLARI • P ha coordinate cartesiane (1, 1) Le coordinate polari di P sono: 2

COORDINATE POLARI • Esiste la seguente relazione tra le coordinate polari e cartesiane di un punto: • si osservi che: 3

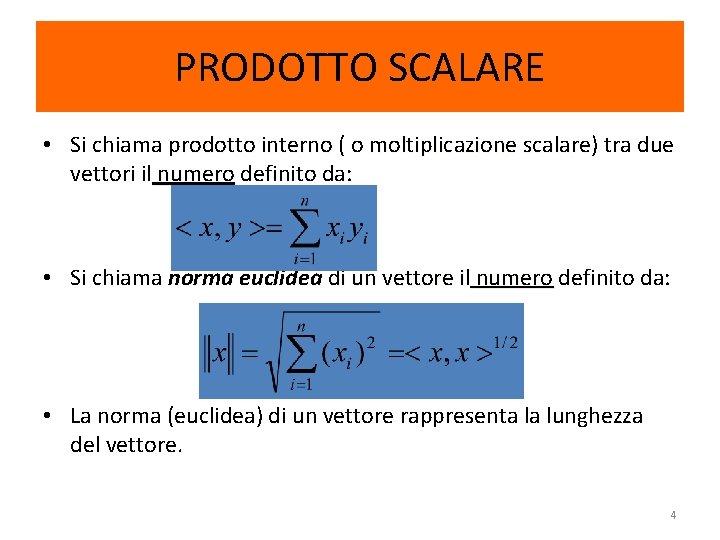
PRODOTTO SCALARE • Si chiama prodotto interno ( o moltiplicazione scalare) scalare tra due vettori il numero definito da: • Si chiama norma euclidea di un vettore ili numero definito da: • La norma (euclidea) di un vettore rappresenta la lunghezza del vettore. 4

NORMA • Possono essere definite altri tipi di norma. • La norma di un vettore è una funzione che soddisfa: 1. 2. 3. 5

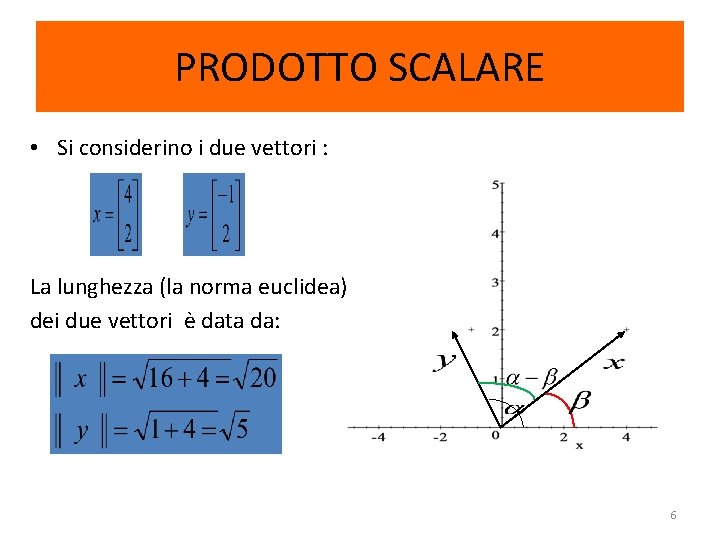
PRODOTTO SCALARE • Si considerino i due vettori : La lunghezza (la norma euclidea) dei due vettori è data da: 6

PRODOTTO SCALARE • Rappresentando le componenti dei 2 vettori in coordinate polari si ha : • Il prodotto scalare dei due vettori diventa: 7

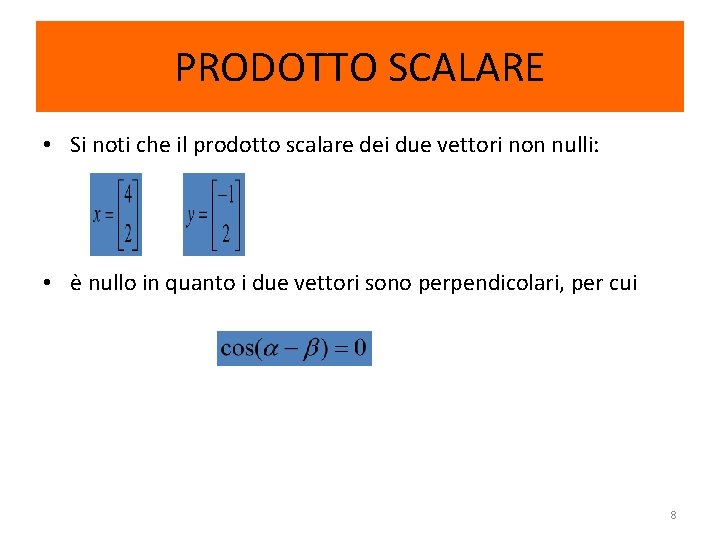
PRODOTTO SCALARE • Si noti che il prodotto scalare dei due vettori non nulli: • è nullo in quanto i due vettori sono perpendicolari, per cui 8

VETTORI ORTONORMALI • Dato un qualunque vettore di norma si può introdurre il vettore normalizzato espresso da: • Due vettori e si dicono ortonormali se sono ortogonali e ciascuno ha norma unitaria. • Se le colonne (o le righe) di una matrice sono a 2 ortonormali la matrice è ortogonale. 9

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Esempio Si considerino i due vettori e costituiti dai prezzi di chiusura settimanale di 2 titoli nelle ultime settimane. Il coefficiente di correlazione lineare tra le due serie di prezzi può essere espresso da: dove rappresenta la media aritmetica dei prezzi di chiusura del titolo i-esimo. 10

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Siano dati 2 titoli i cui prezzi di chiusura nelle ultime 4 settimane sono stati: • Il prezzo medio nelle ultime 4 settimane per ciascun titolo è dato dalla rispettiva media aritmetica 11

ESEMPIO: IL COEFFICIENTE DI CORRELAZIONE LINEARE • Per calcolare il coefficiente di correlazione lineare tra i 2 titoli è utile costruire i 2 vettori: • Per cui si ha: 12

SPAZI VETTORIALI Definizione ed esempi Si considerino 2 insiemi V e K. Si introducano 2 operazioni: • “composizione interna” tra elementi di V; • “composizione esterna” tra elementi di V ed elementi di K. Esempio 1. Composizione interna = somma tra matrici quadrate; Composizione esterna = prodotto di una matrice per uno scalare. 13

SPAZI VETTORIALI Definizione ed esempi Esempio 2 Sia V l’insieme dei polinomi algebrici di grado al massimo n. Composizione interna = somma tra polinomi; Composizione esterna = prodotto di un polinomio per uno scalare. N. B. Controllare cosa succede se V è l’insieme dei polinomi algebrici di grado n. 14

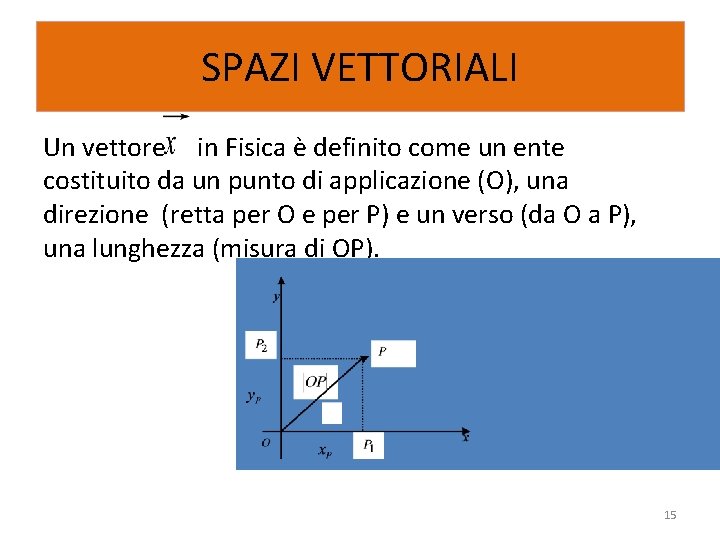
SPAZI VETTORIALI Un vettore in Fisica è definito come un ente costituito da un punto di applicazione (O), una direzione (retta per O e per P) e un verso (da O a P), una lunghezza (misura di OP). 15

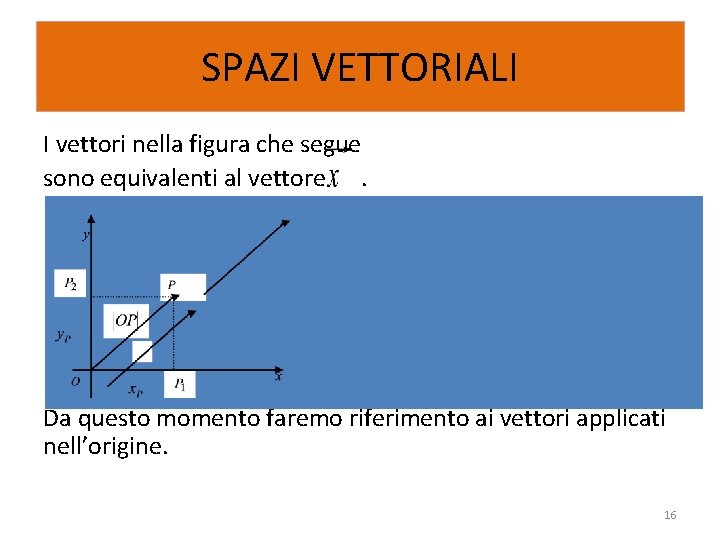
SPAZI VETTORIALI I vettori nella figura che segue sono equivalenti al vettore. Da questo momento faremo riferimento ai vettori applicati nell’origine. 16

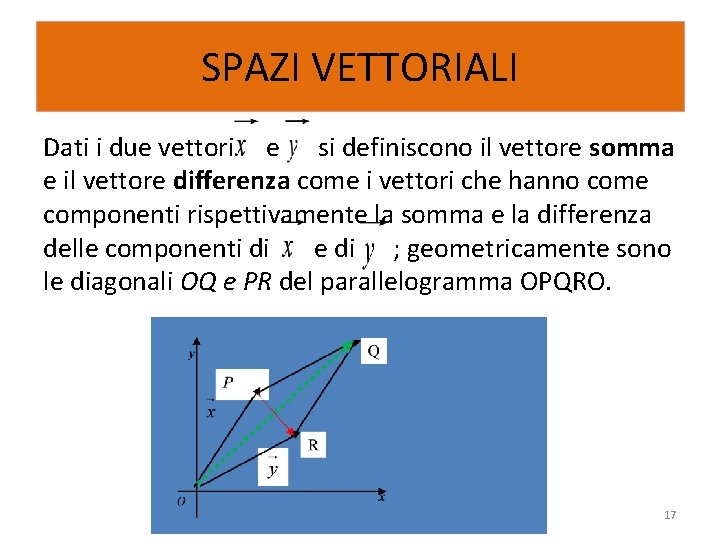
SPAZI VETTORIALI Dati i due vettori e si definiscono il vettore somma e il vettore differenza come i vettori che hanno come componenti rispettivamente la somma e la differenza delle componenti di e di ; geometricamente sono le diagonali OQ e PR del parallelogramma OPQRO. 17

COMBINAZIONE LINEARE Sia V uno spazio vettoriale rispetto al campo degli scalari K. Se W è sottoinsieme di V e W è a sua volta uno spazio vettoriale rispetto al campo degli scalari K, allora si dice che W è sottospazio vettoriale di V. Dati n elementi (vettori) di uno spazio vettoriale V ed n scalari si definisce combinazione lineare il vettore di V espresso da : 18

LINEARE INDIPENDENZA Gli n vettori dello spazio vettoriale V si dicono linearmente indipendenti se risulta se e solo se gli n scalari sono tutti contemporaneamente nulli. Se il vettore nullo si ottiene combinazione lineare di n vettori con coefficienti non tutti nulli allora i vettori si dicono linearmente dipendenti. 19

LINEARE DIPENDENZA Gli n vettori dello spazio vettoriale V sono linearmente dipendenti, e supponiamo che allora , dividendo per ovvero , si ottiene: è combinazione lineare degli altri vettori. 20

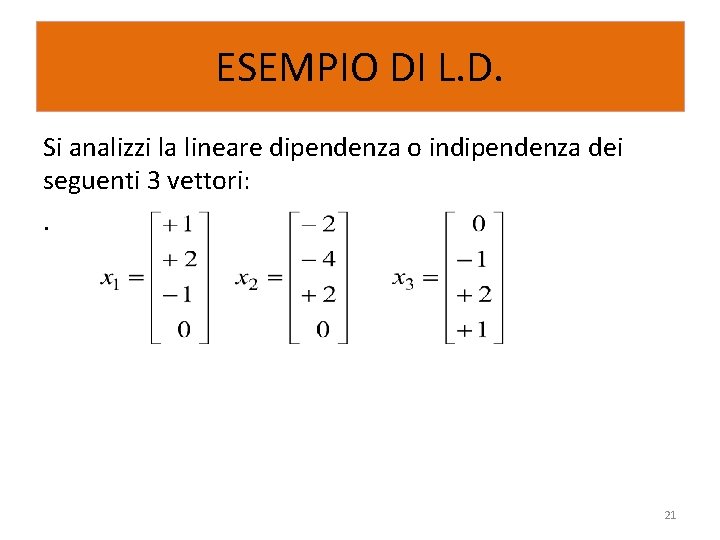
ESEMPIO DI L. D. Si analizzi la lineare dipendenza o indipendenza dei seguenti 3 vettori: . 21

SOLUZIONE DELL’ESEMPIO DI L. D. Per stabilire la dipendenza o indipendenza lineare dei 3 vettori, occorre determinare le soluzioni del sistema: 22

SOLUZIONE DELL’ESEMPIO DI L. D. La matrice dei coefficienti: ha rango 2, quindi il sistema ammette soluzioni : e risulta: 23

ESEMPIO 2 DI L. D. Si vuole esprimere il polinomio come combinazione lineare dei seguenti polinomi: 24

GENERATORI E BASI Dati gli n vettori dello spazio vettoriale V Sia l’insieme delle combinazioni lineari è un sottospazio vettoriale di e i vettori sono chiamati generatori di. Se h vettori tra gli n generatori sono linearmente indipendenti lo spazio vettoriale da essi generato coincide con. I vettori costituiscono una base di 25

GENERATORI E BASI I vettori costituiscono una base di. Il numero h dei vettori della base viene chiamato dimensione di. Dato un qualunque vettore esso può essere scritto come e i coefficienti della combinazione lineare vengono denominati coordinate (sono uniche!) del vettore rispetto alla base. Dato lo spazio vettoriale di dimensione h, esistono più basi. 26

GENERATORI E BASI Si considerino 2 basi di Un vettore può essere espresso nelle 2 basi da Ovvero come: Dove : 27

GENERATORI E BASI Uguagliando si ha da cui : ovvero La matrice cambiamento di base. è denominata matrice di 28

ESEMPIO DI GENERATORI E BASI Si consideri lo spazio vettoriale V dei polinomi algebrici di grado minore o uguale a 3: Si considerino i vettori di V : Essi sono generatori di V. Non sono linearmente indipendenti. I vettori sono linearmente indipendenti. 29

BASE CANONICA Si consideri lo spazio vettoriale V delle matrici quadrate di ordine 2. Una base è costituita da Si considerino i vettori di V : Sono una base per V, detta canonica. 30

ESEMPIO DI CAMBIAMENTO DI BASE Si considerino i 2 vettori dello spazio vettoriale delle matrici 2 x 1: Si determini la matrice di cambiamento di base rispetto alla base canonica. 31

TRASFORMAZIONI LINEARI Dati due spazi vettoriali W e si definisce trasformazione lineare di W in ogni funzione tale che: • • Nucleo di T, ker(T), l’insieme dei vettori di W che hanno come immagine il vettore nullo di. Immagine di T, Im(T), l’insieme di vettori di che provengono da vettori di W. 32

ESEMPIO DI T. L. Dati i due spazi vettoriali e si consideri la trasformazione lineare di in : • L’immagine della t. l. è l’insieme. Il nucleo di T, ker(T), è l’insieme dei vettori di che hanno come immagine il vettore nullo di , ovvero Da cui si ricava: Quindi 33

ESEMPIO DI T. L. Dati i due spazi vettoriali e si dimostri che la legge seguente è una trasformazione lineare : • dove Analogamente si dimostra che la trasformazione che associa al vettore la media aritmetica delle componenti è una trasformazione lineare: 34

ESEMPIO DI T. L. Si determini la trasformazione lineare tra e che fa corrispondere ad ogni vettore il vettore degli scarti dalla media aritmetica. • 35

TEOREMA DI RAPPRESENTAZIONE Si consideri la trasformazione lineare tra i due spazi vettoriali e , si può dimostrare il seguente teorema di rappresentazione: Se La trasformazione lineare viene denominata isomorfismo. 36

EQUAZIONE CARATTERISTICA L’equazione caratteristica è data da: ovvero: Le soluzioni vengono denominate autovalori. Le soluzioni del sistema: vengono denominate autovettori corrispondenti all’autovalore. 37

EQUAZIONE CARATTERISTICA Per l’equazione caratteristica valgono i seguenti teoremi: 1. Il coefficiente della potenza può essere ottenuto dalla somma degli minori principali di ordine i della matrice A moltiplicata per. 2. Il coefficiente della potenza può essere ottenuto dalla somma degli prodotti degli autovalori presi i alla volta moltiplicata per. 38

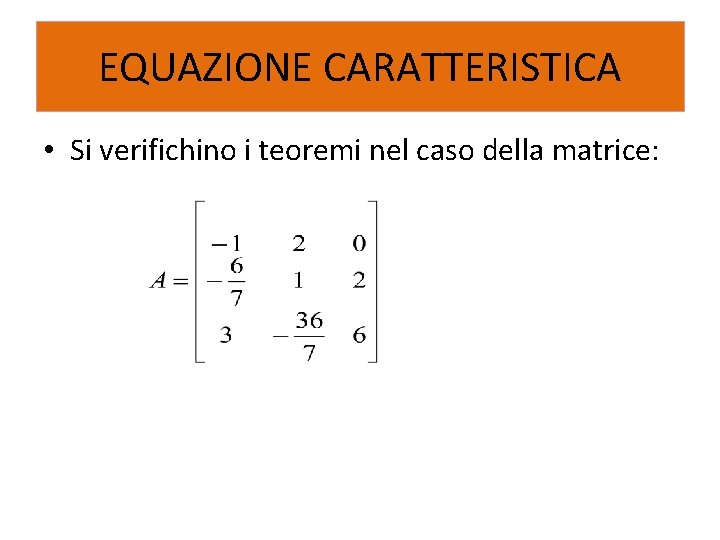
EQUAZIONE CARATTERISTICA • Si verifichino i teoremi nel caso della matrice:

EQUAZIONE CARATTERISTICA Teorema 3 “Una matrice quadrata ammette l’autovalore nullo se e solo il determinante è nullo”. Teorema 4 “Ogni matrice quadrata soddisfa la sua equazione caratteristica”.

EQUAZIONE CARATTERISTICA Teorema 5 “Se il rango di una matrice quadrata è r allora l’autovalore nullo ha molteplicità algebrica ”. Teorema 6 “Gli autovalori di una matrice triangolare coincidono con gli elementi della diagonale principale”.

MOLTEPLICITA’ Teorema 7 “Ad autovalori diversi corrispondono autovettori linearmente indipendenti”. Molteplicità algebrica Molteplicità geometrica Teorema 8 “La molteplicità algebrica dell’autovalore è maggiore o uguale alla moteplicità geometrica ”.

MATRICE MODALE Si definisce matrice modale della matrice A la matrice le cui colonne sono costituite dagli autovettori della matrice A” Teorema 9 “Gli autovalori di una matrice simmetrica sono reali” Teorema 10 “La matrice modale di una matrice simmetrica è ortogonale. ”

SISTEMI DI EQUAZIONI DIFFERENZIALI Un sistema di equazioni differenziali lineari è:

SISTEMI DI EQUAZIONI DIFFERENZIALI Un sistema di equazioni differenziali lineari omogeneo è:

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 2.

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 3.

SISTEMI DI EQUAZIONI DIFFERENZIALI Esempio 4.