COORDINATE PLANE FORMULAS Midpoint formula x 2 y

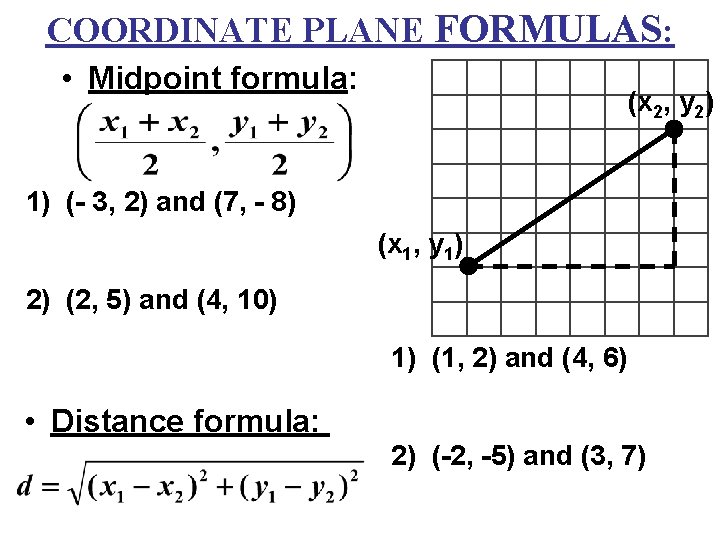
COORDINATE PLANE FORMULAS: • Midpoint formula: (x 2, y 2) 1) (- 3, 2) and (7, - 8) (x 1, y 1) 2) (2, 5) and (4, 10) 1) (1, 2) and (4, 6) • Distance formula: 2) (-2, -5) and (3, 7)

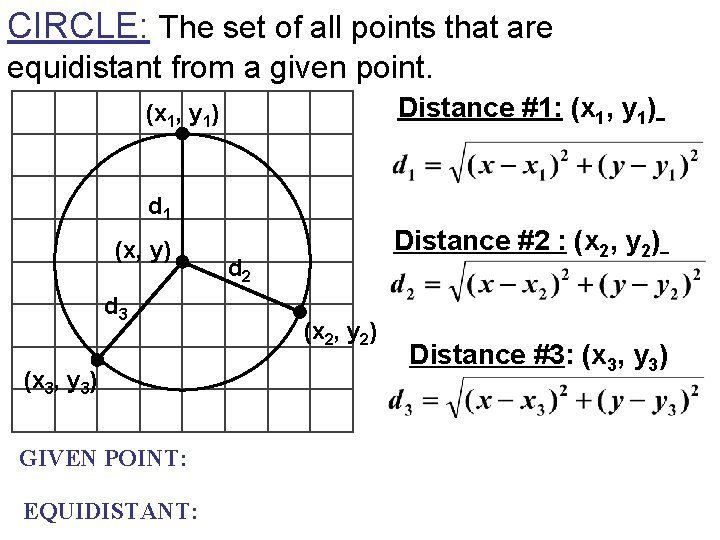
CIRCLE: The set of all points that are equidistant from a given point. Distance #1: (x 1, y 1) d 1 (x, y) d 3 (x 3, y 3) GIVEN POINT: EQUIDISTANT: Distance #2 : (x 2, y 2) d 2 (x 2, y 2) Distance #3: (x 3, y 3)

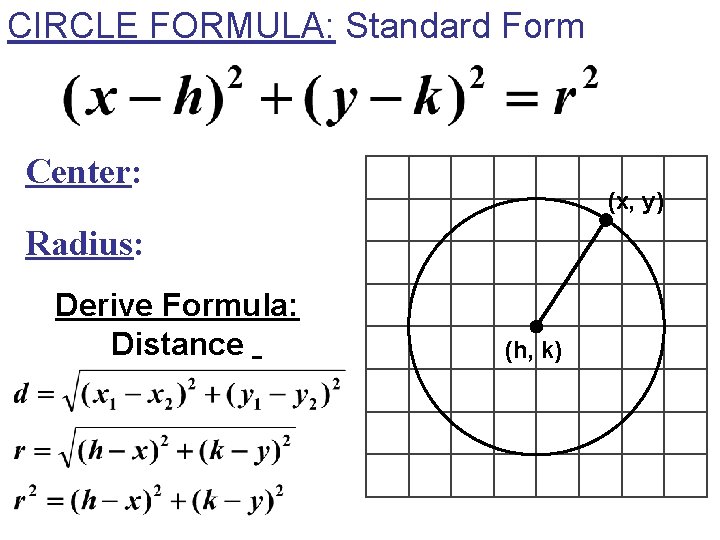
CIRCLE FORMULA: Standard Form Center: (x, y) Radius: Derive Formula: Distance (h, k)

PRACTICE #1: Interpret Equation of a Circle 1. IDENTIFY the center and radius in the equation. a. Center: _____ Radius: ____ b. Center: _____ Radius: ____ c. Center: _____ Radius: ____

PRACTICE #2: Write the Equation of a Circle 2. Write an equation of the circle with a center (-1, 3) and radius of 6. 3. Write the equation of the circle pictured to the right

PRACTICE #3: Write the equation of the circle given the endpoints of a diameter. 4. (-1, 7) and (5, -1) 5. (-3, 4) and (-7, -6)

PRACTICE #3 : Continued 6. (-3, -5) and (6, 2) 7. (4, 8) and (4, -2)

HOW TO: Writing Circles in standard form Step #1: Group x and y terms separately together Step #2: Move the constant term to the opposite side Step #3: Complete the square for x’s and y’s (Add Both to Right Side) Step #1: Step #2: Step #3: Standard Form: Center: (-4, 6) Radius: 9

PRACTICE #4: Writing Circles in Standard Form Write in standard form, find the radius and center. Sketch a graph [A] [B]

PRACTICE #4: Continued Write in standard form, find the radius and center. Sketch a Graph. [C] [D]

PRACTICE #4: Continued Write in standard form, find the radius and center. [E] [F]

PRACTICE #5: Equations given the a Tangent TANGENT: A line intersecting at exactly one point with another curve. Additional Fact: Tangents are perpendicular to the curve. Write the equation of the circle given its tangency to an axis. [A] Center: (-4, -3) Tangent to x-axis [B] Center: (3, 5) tangent to y-axis