Convolution Neural Networks with Daniel L Silver Ph

Convolution Neural Networks with Daniel L. Silver, Ph. D. Christian Frey, BBA April 11 -12, 2017 Slides based on originals by Yann Le. Cun

Convolution Neural Networks Fundamental CNNs take advantage of knowledge that the architect has about the problem’s input space We know that pixels in an image that are adjacent to each other are related – will have about he same color and brightness We can use this background knowledge as a source of inductive bias to help develop better NN models 2

Receptive Fields The receptive field of an individual sensory neuron is the particular region of the sensory space (e. g. , the body surface, or the retina) in which a stimulus will trigger the firing of that neuron. q It is a feature detector (image line orientation, sound frequency) How do we design “proper” receptive fields for the input neurons? Consider a task with image inputs q q Receptive fields should give expressive features from the raw input to the system How would you design the receptive fields for this problem? 3

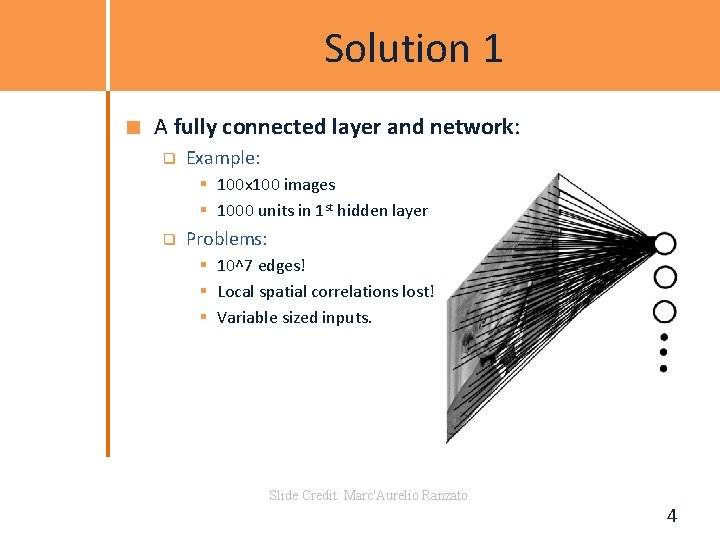
Solution 1 A fully connected layer and network: q Example: § 100 x 100 images § 1000 units in 1 st hidden layer q Problems: § 10^7 edges! § Local spatial correlations lost! § Variable sized inputs. Slide Credit: Marc'Aurelio Ranzato 4

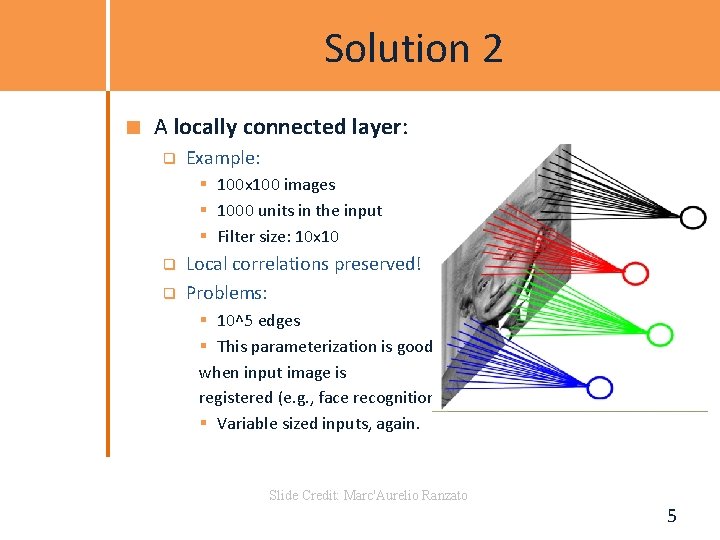
Solution 2 A locally connected layer: q Example: § 100 x 100 images § 1000 units in the input § Filter size: 10 x 10 q q Local correlations preserved! Problems: § 10^5 edges § This parameterization is good when input image is registered (e. g. , face recognition). § Variable sized inputs, again. Slide Credit: Marc'Aurelio Ranzato 5

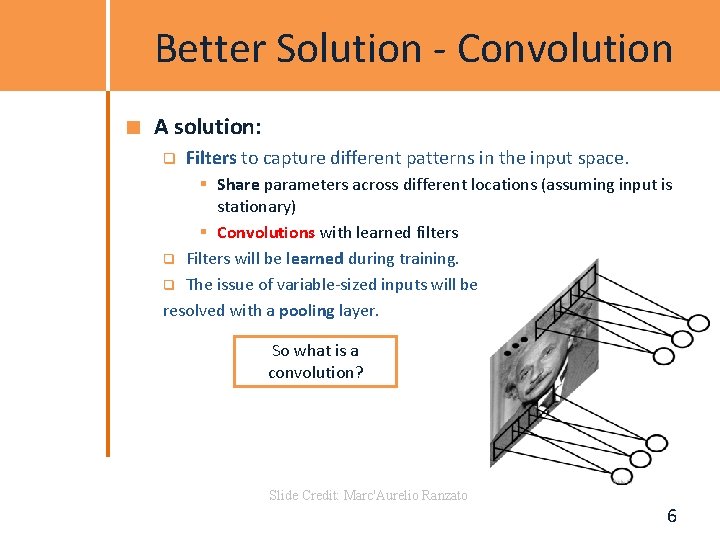
Better Solution - Convolution A solution: q Filters to capture different patterns in the input space. § Share parameters across different locations (assuming input is stationary) § Convolutions with learned filters q Filters will be learned during training. q The issue of variable-sized inputs will be resolved with a pooling layer. So what is a convolution? Slide Credit: Marc'Aurelio Ranzato 6

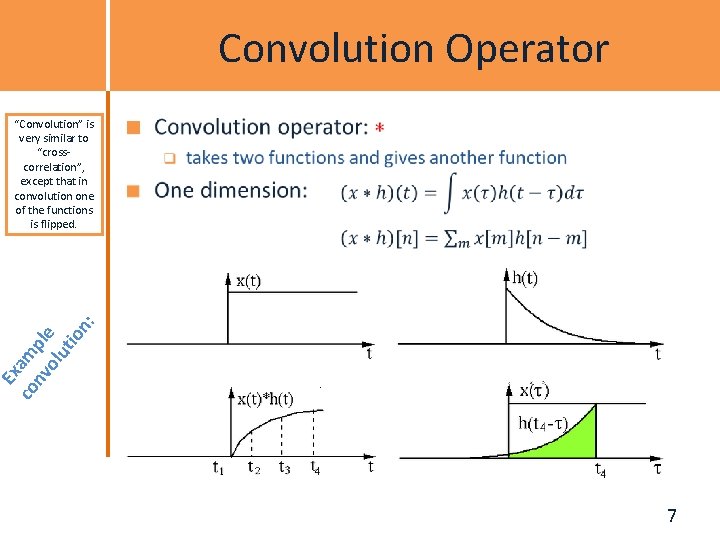
Convolution Operator Ex co am nv ple ol ut io n: “Convolution” is very similar to “crosscorrelation”, except that in convolution one of the functions is flipped. 7

Convolution Operator (2) Convolution in two dimension: q q The same idea: flip one matrix and slide it on the other matrix Example: Sharpen kernel: Try other kernels: http: //setosa. io/ev/image-kernels/ 8

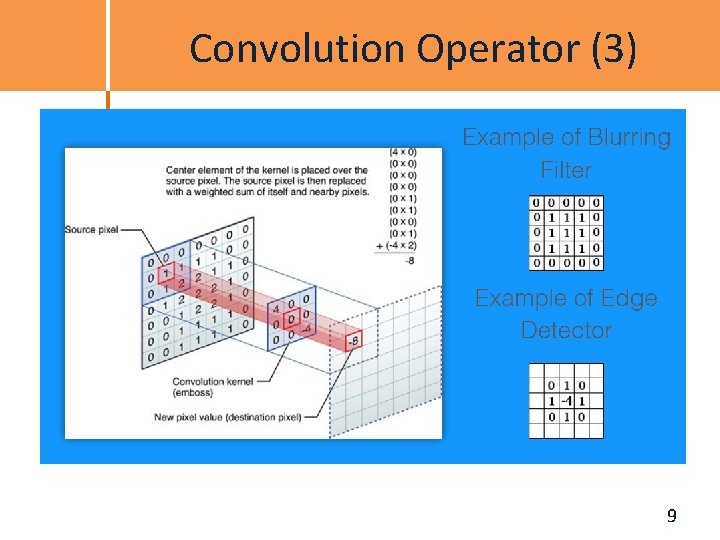
Convolution Operator (3) 9

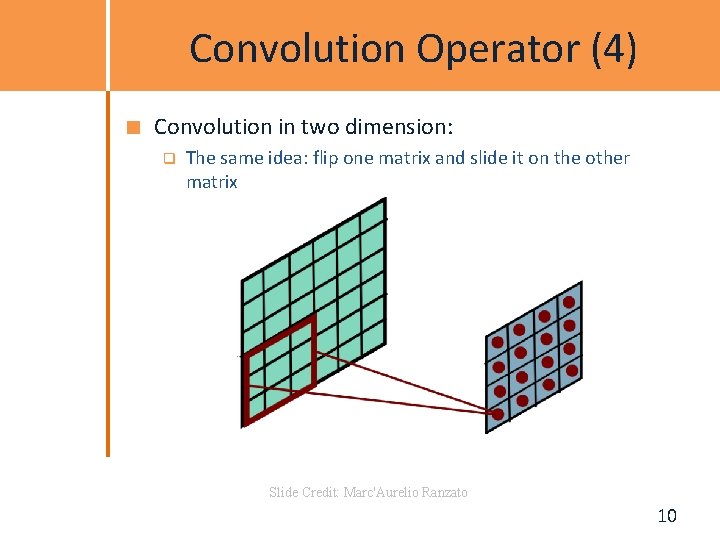
Convolution Operator (4) Convolution in two dimension: q The same idea: flip one matrix and slide it on the other matrix Slide Credit: Marc'Aurelio Ranzato 10

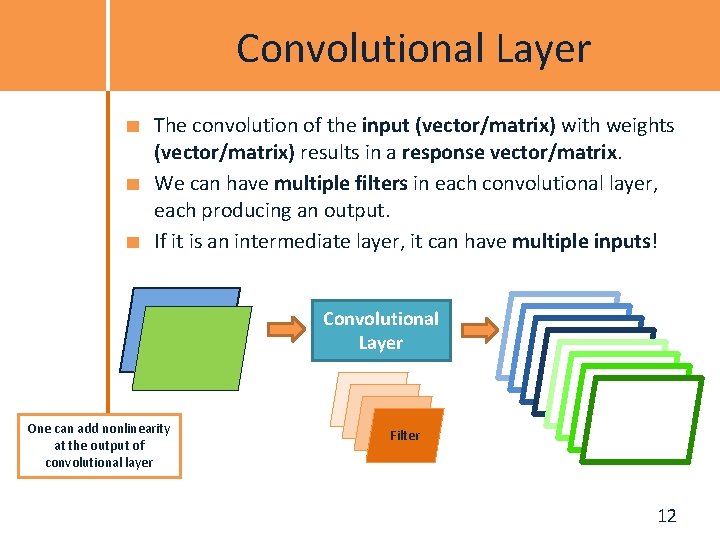
Convolutional Layer The convolution of the input (vector/matrix) with weights (vector/matrix) results in a response vector/matrix. We can have multiple filters in each convolutional layer, each producing an output. If it is an intermediate layer, it can have multiple inputs! Convolutional Layer One can add nonlinearity at the output of convolutional layer Filter 12

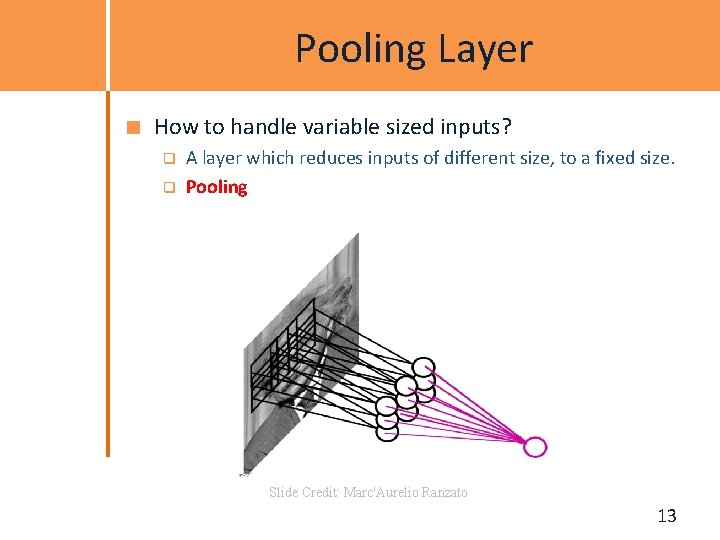
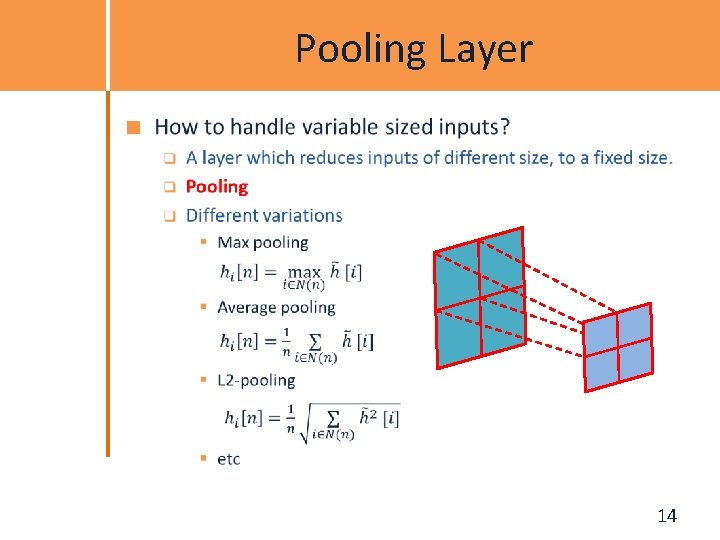
Pooling Layer How to handle variable sized inputs? q q A layer which reduces inputs of different size, to a fixed size. Pooling Slide Credit: Marc'Aurelio Ranzato 13

Pooling Layer 14

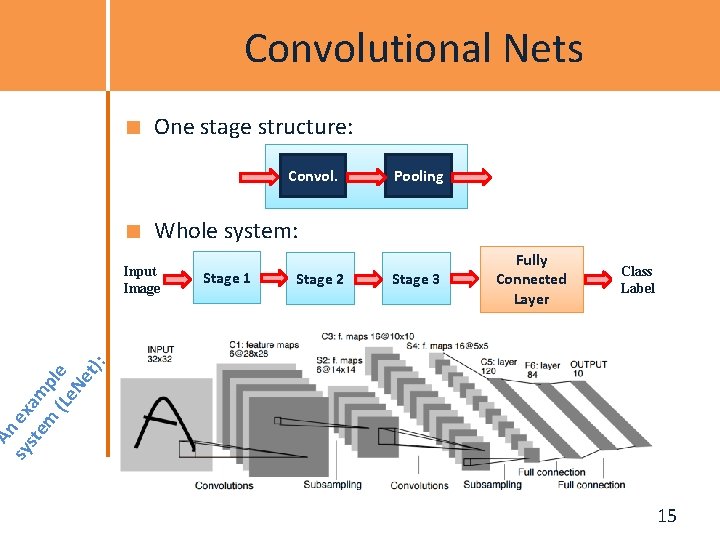
Convolutional Nets One stage structure: Convol. Pooling Whole system: Stage 1 Stage 2 Stage 3 Fully Connected Layer Class Label An sy ex ste am m pl (Le e Ne t): Input Image Slide Credit: Druv Bhatra 15

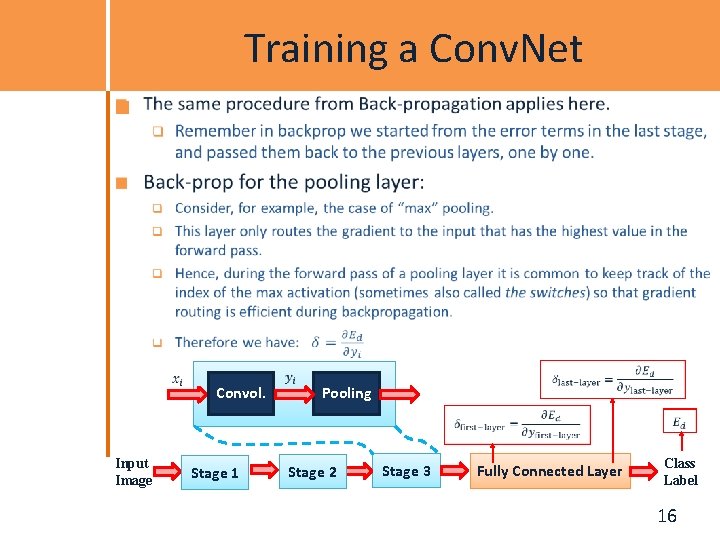
Training a Conv. Net Convol. Input Image Stage 1 Pooling Stage 2 Stage 3 Fully Connected Layer Class Label 16

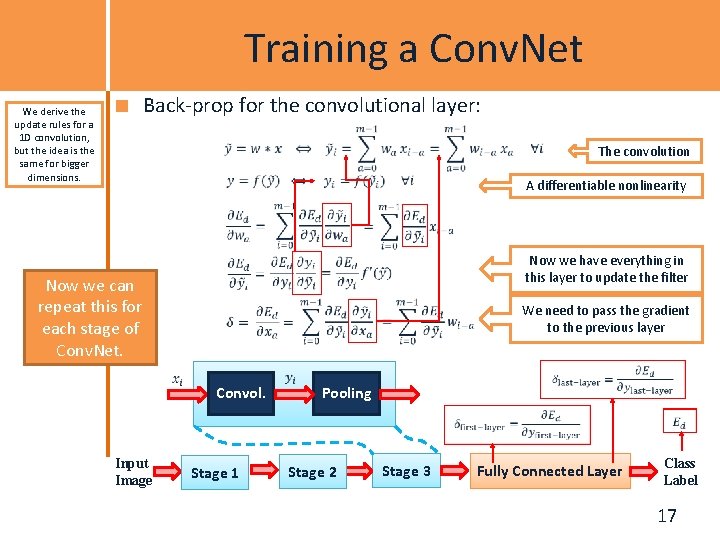
Training a Conv. Net Back-prop for the convolutional layer: We derive the update rules for a 1 D convolution, but the idea is the same for bigger dimensions. The convolution A differentiable nonlinearity Now we have everything in this layer to update the filter Now we can repeat this for each stage of Conv. Net. We need to pass the gradient to the previous layer Convol. Input Image Stage 1 Pooling Stage 2 Stage 3 Fully Connected Layer Class Label 17

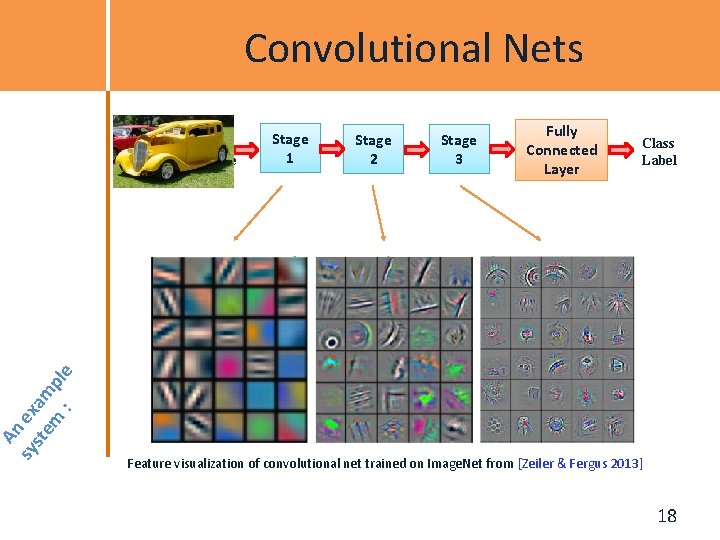
An sy ex ste am m pl e : Convolutional Nets Input Image Stage 1 Stage 2 Stage 3 Fully Connected Layer Class Label Feature visualization of convolutional net trained on Image. Net from [Zeiler & Fergus 2013] 18

Conv. Net roots Fukushima, 1980 s designed network with same basic structure but did not train by backpropagation. The first successful applications of Convolutional Networks by Yann Le. Cun in 1990's (Le. Net) Was used to read zip codes, digits, etc. Many variants nowadays, but the core idea is the same q Example: a system developed in Google (Goog. Le. Net) § Compute different filters § Compose one big vector from all of them § Layer this iteratively De m o! q See more: http: //arxiv. org/pdf/1409. 4842 v 1. pdf 19

Depth matters Slide from [Kaiming He 2015] 20

Practical Tips Before large scale experiments, test on a small subset of the data and check the error should go to zero. q Overfitting on small training Visualize features (feature maps need to be uncorrelated) and have high variance Bad training: many hidden units ignore the input and/or exhibit strong correlations. Figure Credit: Marc'Aurelio Ranzato 21

Debugging Training diverges: q q Learning rate may be too large → decrease learning rate Back. Prop is buggy → numerical gradient checking Loss is minimized but accuracy is low q Check loss function: Is it appropriate for the task you want to solve? Does it have degenerate solutions? NN is underperforming / under-fitting q Compute number of parameters → if too small, make network larger NN is too slow q Compute number of parameters → Use distributed framework, use GPU, make network smaller Many of these points apply to many machine learning models, no just neural networks. 22

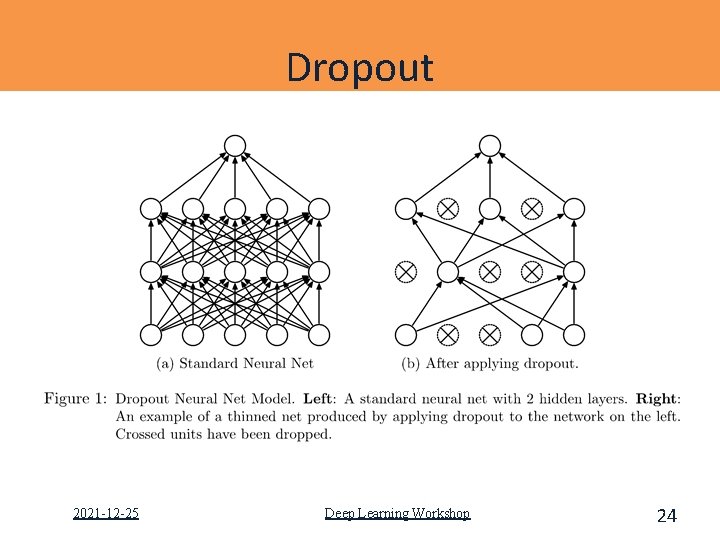
Dropout One or more neural network nodes is switched off once in a while so that it will not interact with the network (it weights cannot be updated, nor affect the learning of the other network nodes). Learned weights of the nodes become somewhat more insensitive to the weights of the other nodes and learn to decide somewhat more by their own (and less dependent on the other nodes they're connected to). Helps the network to generalize better and increase accuracy since the (possibly somewhat dominating) influence of a single node is decreased by dropout. 2021 -12 -25 Deep Learning Workshop 23

Dropout 2021 -12 -25 Deep Learning Workshop 24

Dropout is a form of regularisation How does it work? It essentially forces an artificial neural network to learn multiple independent representations of the same data by alternately randomly disabling neurons in the learning phase. What is the effect of this? The effect of this is that neurons are prevented from coadapting too much which makes overfitting less likely. Why does this happen? The reason that this works is comparable to why using the mean outputs of many separately trained neural networks to reduces overfitting. 2021 -12 -25 Deep Learning Workshop 25

TUTORIAL 9 Develop and train a CNN network using Keras and Tensorflow (Python code)

References https: //ujjwalkarn. me/2016/08/11/intuitiveexplanation-convnets/ https: //adeshpande 3. github. io/A-Beginner's-Guide. To-Understanding-Convolutional-Neural-Networks. Part-2/ 2021 -12 -25 Deep Learning Workshop 27

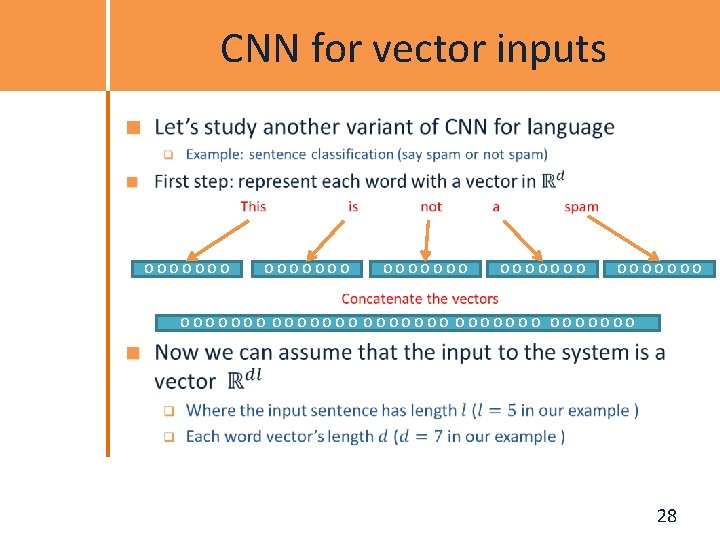
CNN for vector inputs OOOOOOO OOOOOOO OOOOOOO 28

A lay con er vol ut io na l Convolutional Layer on vectors OOOOOOO O O O O O O O OOOOOOO OOOOOOO 29

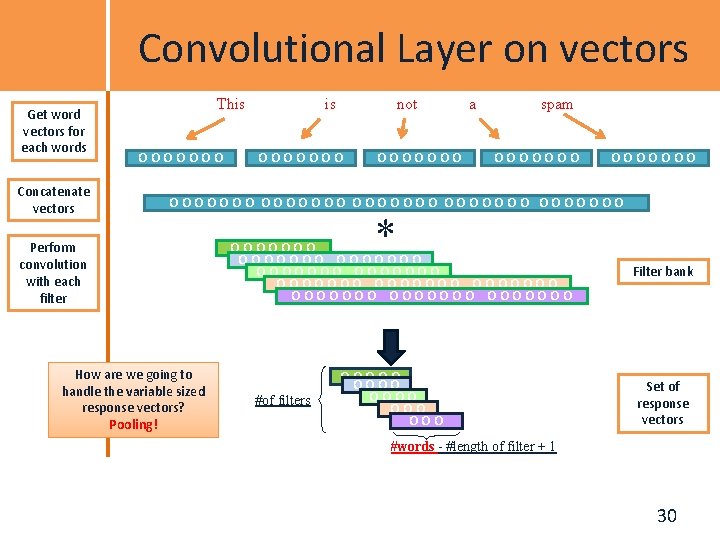
Convolutional Layer on vectors Get word vectors for each words Concatenate vectors This OOOOOOO is not OOOOOOO a spam OOOOOOO OOOOOOO Perform convolution with each filter How are we going to handle the variable sized response vectors? Pooling! * OOOOOOO OOOOOOO OOOOOOO #of filters OOOOO OOO Filter bank Set of response vectors #words - #length of filter + 1 30

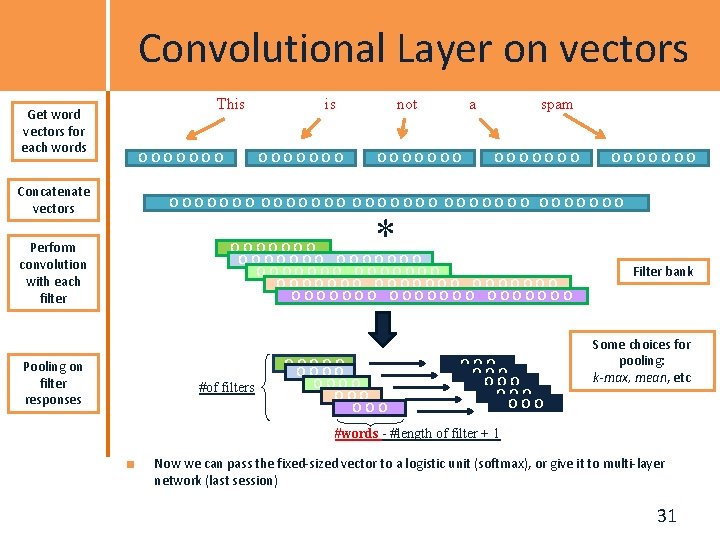
Convolutional Layer on vectors Get word vectors for each words Concatenate vectors Perform convolution with each filter Pooling on filter responses This OOOOOOO not a OOOOOOO spam OOOOOOO OOOOOOO * OOOOOOO OOOOOOO OOOOOOO #of filters OOOOO OOO OOO OOO Filter bank Some choices for pooling: k-max, mean, etc #words - #length of filter + 1 Now we can pass the fixed-sized vector to a logistic unit (softmax), or give it to multi-layer network (last session) 31