Convex Relaxation for Polynomial Optimization Application to Power

Convex Relaxation for Polynomial Optimization: Application to Power Systems and Decentralized Control Javad Lavaei Department of Electrical Engineering Columbia University

Outline v Convex relaxation for highly structured optimization (Joint work with: Somayeh Sojoudi) v Optimization over power networks (Joint work with: Steven Low, David Tse, Stephen Boyd, Somayeh Sojoudi, Ramtin Madani, Baosen Zhang, Matt Kraning, Eric Chu) v Optimal decentralized control (Joint work with: Ghazal Fazelnia and Ramtin Madani) v General theory for polynomial optimization (Joint work with: Ramtin Madani, Somayeh Sojoudi and Ghazal Fazelnia) Javad Lavaei, Columbia University 2

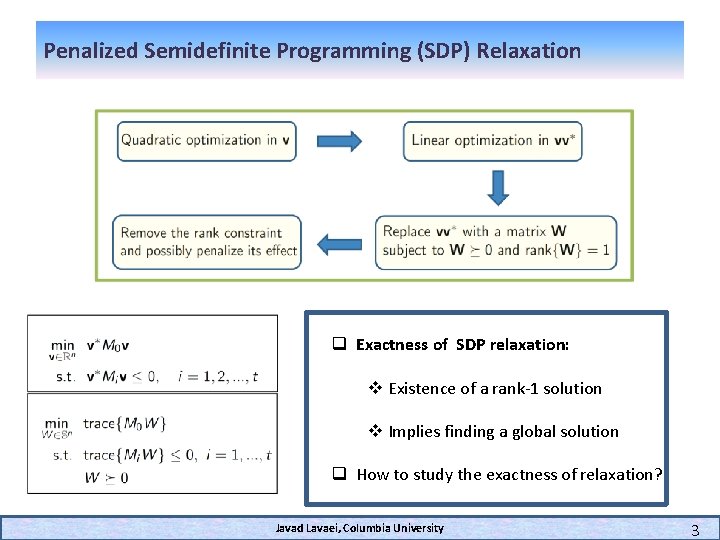
Penalized Semidefinite Programming (SDP) Relaxation q Exactness of SDP relaxation: v Existence of a rank-1 solution v Implies finding a global solution q How to study the exactness of relaxation? Javad Lavaei, Columbia University 3

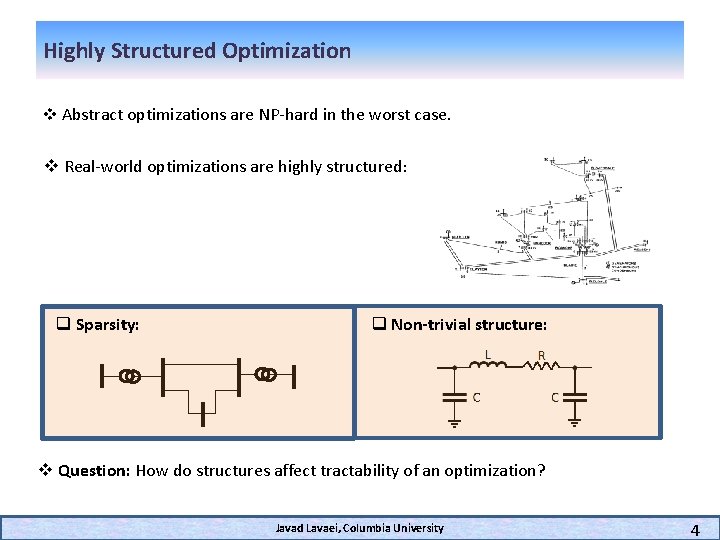
Highly Structured Optimization v Abstract optimizations are NP-hard in the worst case. v Real-world optimizations are highly structured: q Sparsity: q Non-trivial structure: v Question: How do structures affect tractability of an optimization? Javad Lavaei, Columbia University 4

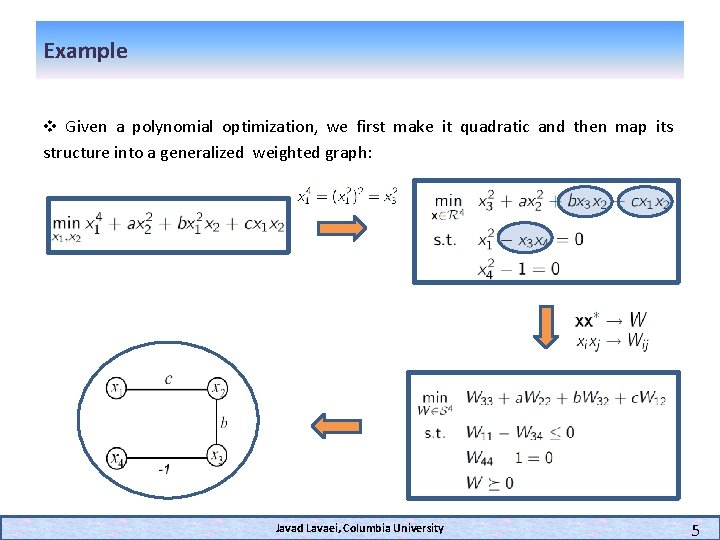
Example v Given a polynomial optimization, we first make it quadratic and then map its structure into a generalized weighted graph: Javad Lavaei, Columbia University 5

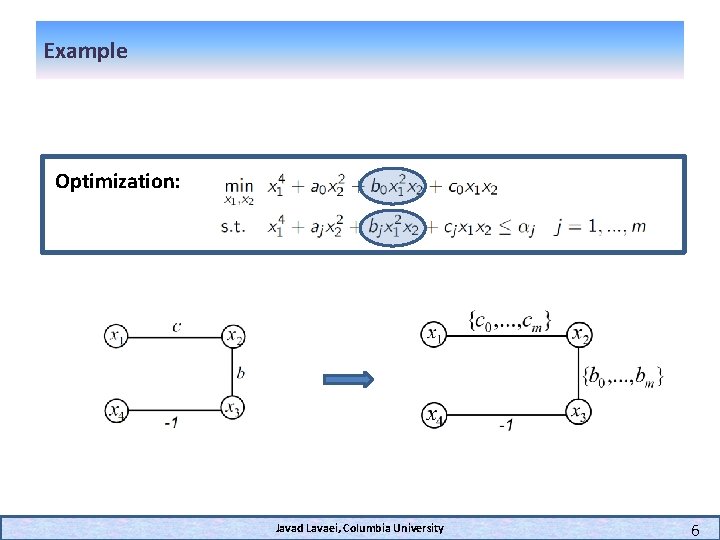
Example Optimization: Javad Lavaei, Columbia University 6

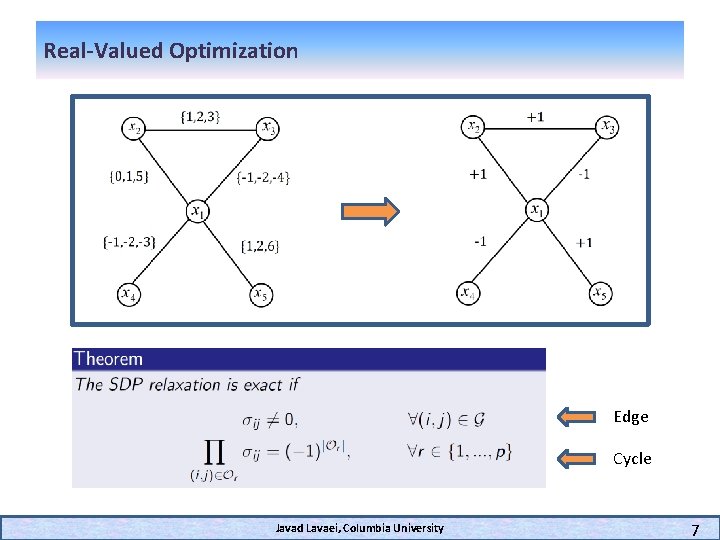
Real-Valued Optimization Edge Cycle Javad Lavaei, Columbia University 7

Complex-Valued Optimization v Real-valued case: “T “ is sign definite if its elements are all negative or all positive. v Complex-valued case: “T “ is sign definite if T and –T are separable in R 2: Javad Lavaei, Columbia University 8

Complex-Valued Optimization v Consider a real matrix M: v Polynomial-time solvable for weakly-cyclic bipartite graphs. Javad Lavaei, Columbia University 9

Outline v Convex relaxation for highly structured optimization (Joint work with: Somayeh Sojoudi) v Optimization over power networks (Joint work with: Steven Low, David Tse, Stephen Boyd, Somayeh Sojoudi, Ramtin Madani, Baosen Zhang, Matt Kraning, Eric Chu) v Optimal decentralized control (Joint work with: Ghazal Fazelnia and Ramtin Madani) v General theory for polynomial optimization (Joint work with: Ramtin Madani, Somayeh Sojoudi and Ghazal Fazelnia) Javad Lavaei, Columbia University 10

Power Networks q Optimizations: § Optimal power flow (OPF) § Security-constrained OPF § State estimation § Network reconfiguration § Unit commitment § Dynamic energy management q Issue of non-convexity: § Discrete parameters § Nonlinearity in continuous variables q Transition from traditional grid to smart grid: § More variables (10 X) § Time constraints (100 X) Javad Lavaei, Columbia University 11

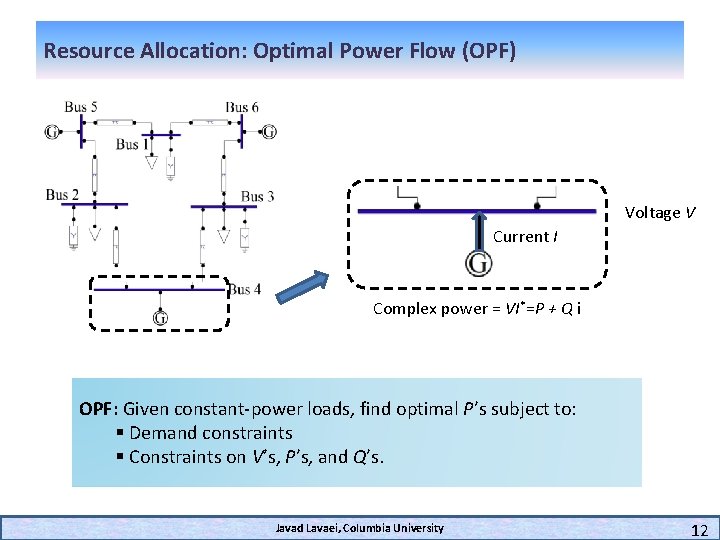
Resource Allocation: Optimal Power Flow (OPF) Voltage V Current I Complex power = VI*=P + Q i OPF: Given constant-power loads, find optimal P’s subject to: § Demand constraints § Constraints on V’s, P’s, and Q’s. Javad Lavaei, Columbia University 12

Broad Interest in Optimal Power Flow q OPF-based problems solved on different time scales: § Electricity market § Real-time operation § Security assessment § Transmission planning q Existing methods based on linearization or local search q Question: How to find the best solution using a scalable robust algorithm? q Huge literature since 1962 by power, OR and Econ people Javad Lavaei, Columbia University 13

Optimal Power Flow Cost Operation Flow Balance Javad Lavaei, Columbia University 14

Project 1: How to solve a given OPF in polynomial time? (joint work with Steven Low) q A sufficient condition to globally solve OPF: § Numerous randomly generated systems § IEEE systems with 14, 30, 57, 118, 300 buses § European grid q Various theories: It holds widely in practice Javad Lavaei, Columbia University 15

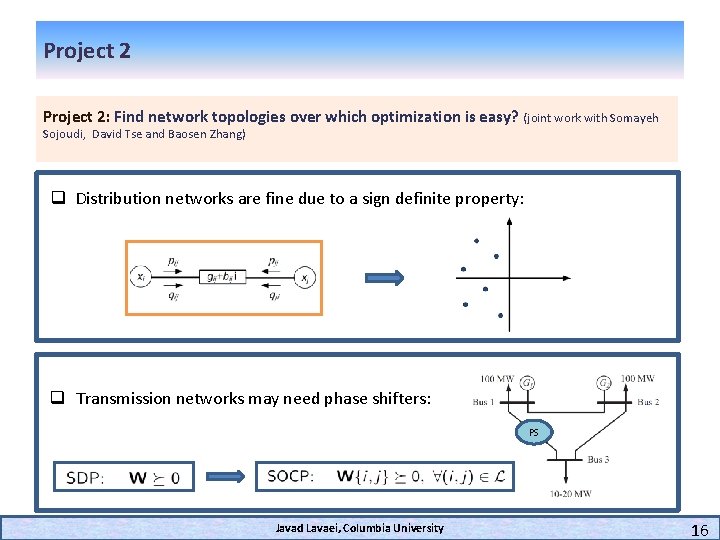
Project 2: Find network topologies over which optimization is easy? (joint work with Somayeh Sojoudi, David Tse and Baosen Zhang) q Distribution networks are fine due to a sign definite property: q Transmission networks may need phase shifters: PS Javad Lavaei, Columbia University 16

Project 3: How to design a distributed algorithm for solving OPF? (joint work with Stephen Boyd, Eric Chu and Matt Kranning) q A practical (infinitely) parallelizable algorithm using ADMM. q It solves 10, 000 -bus OPF in 0. 85 seconds on a single core machine. Javad Lavaei, Columbia University 17

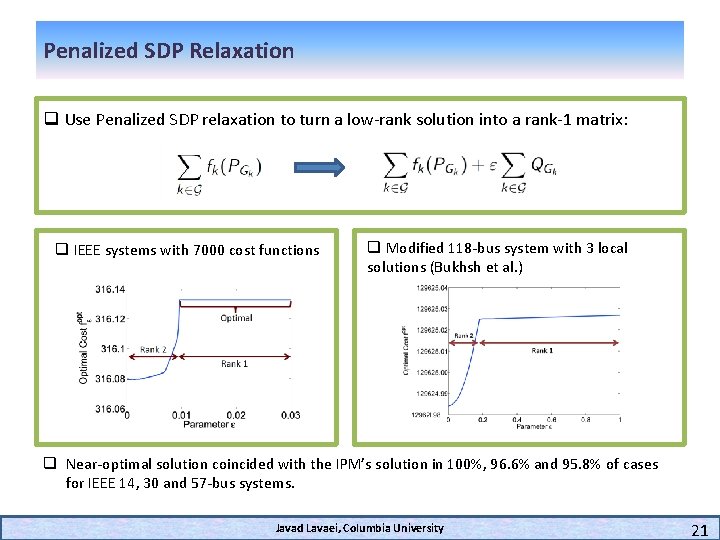
Project 4: How to do optimization for mesh networks? (joint work with Ramtin Madani and Somayeh Sojoudi) q Observed that equivalent formulations might be different after relaxation. q Upper bounded the rank based on the network topology. q Developed a penalization technique. q Verified its performance on IEEE systems with 7000 cost functions. Javad Lavaei, Columbia University 18

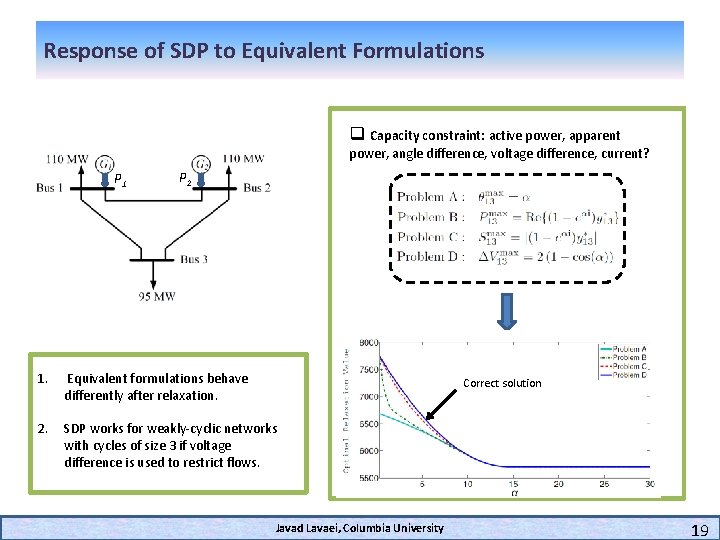
Response of SDP to Equivalent Formulations q Capacity constraint: active power, apparent power, angle difference, voltage difference, current? P 1 P 2 1. Equivalent formulations behave differently after relaxation. 2. SDP works for weakly-cyclic networks with cycles of size 3 if voltage difference is used to restrict flows. Correct solution Javad Lavaei, Columbia University 19

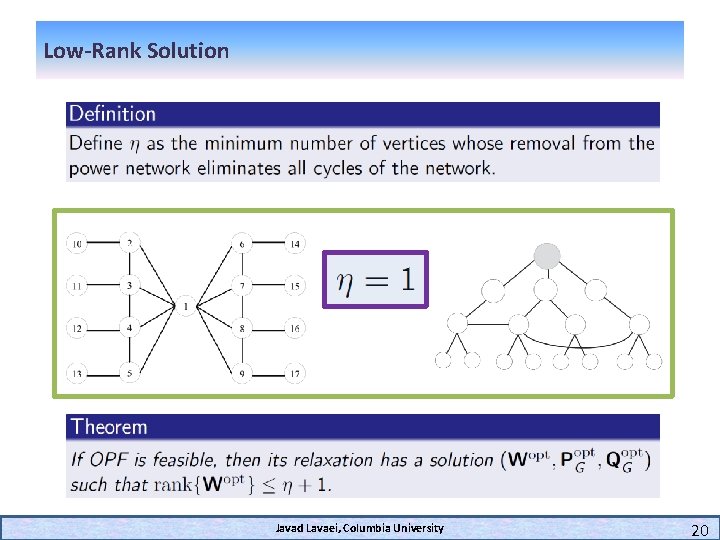
Low-Rank Solution Javad Lavaei, Columbia University 20

Penalized SDP Relaxation q Use Penalized SDP relaxation to turn a low-rank solution into a rank-1 matrix: q IEEE systems with 7000 cost functions q Modified 118 -bus system with 3 local solutions (Bukhsh et al. ) q Near-optimal solution coincided with the IPM’s solution in 100%, 96. 6% and 95. 8% of cases for IEEE 14, 30 and 57 -bus systems. Javad Lavaei, Columbia University 21

Outline v Convex relaxation for highly structured optimization (Joint work with: Somayeh Sojoudi) v Optimization over power networks (Joint work with: Steven Low, David Tse, Stephen Boyd, Somayeh Sojoudi, Ramtin Madani, Baosen Zhang, Matt Kraning, Eric Chu) v Optimal decentralized control (Joint work with: Ghazal Fazelnia and Ramtin Madani) v General theory for polynomial optimization (Joint work with: Ramtin Madani, Somayeh Sojoudi and Ghazal Fazelnia) Javad Lavaei, Columbia University 22

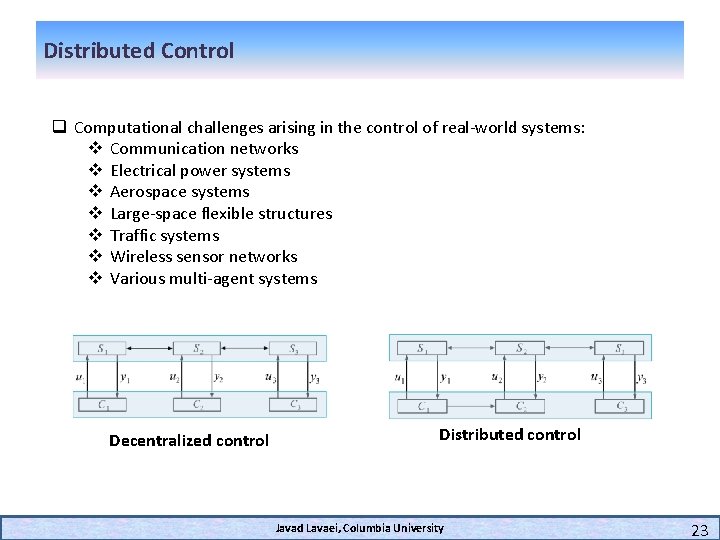
Distributed Control q Computational challenges arising in the control of real-world systems: v Communication networks v Electrical power systems v Aerospace systems v Large-space flexible structures v Traffic systems v Wireless sensor networks v Various multi-agent systems Decentralized control Distributed control Javad Lavaei, Columbia University 23

Optimal Decentralized Control Problem q Optimal centralized control: Easy (LQR, LQG, etc. ) q Optimal distributed control (ODC): NP-hard (Witsenhausen’s example) q Consider the time-varying system: q The goal is to design a structured controller Javad Lavaei, Columbia University to minimize 24

Two Quadratic Formulations in Static Case q Formulation in time domain: v Stack the free parameters of K in a vector h. v Define v as: q Formulation in Lypunov domain: v Consider the BMI constraint: v Define v as: Javad Lavaei, Columbia University 25

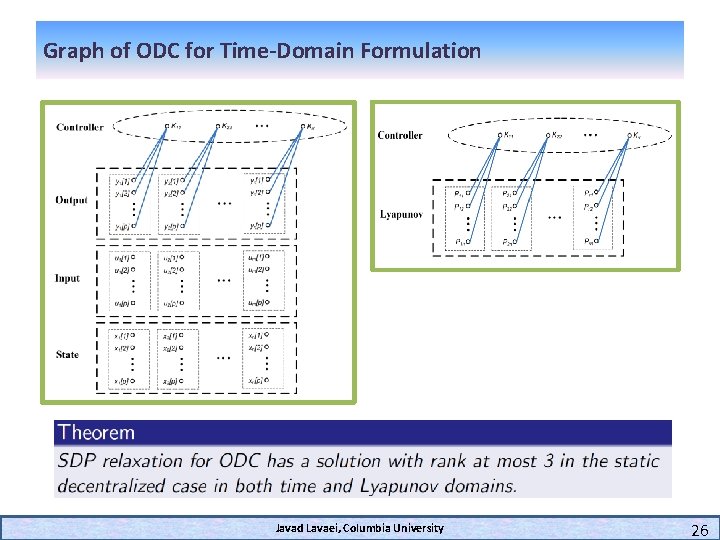
Graph of ODC for Time-Domain Formulation Javad Lavaei, Columbia University 26

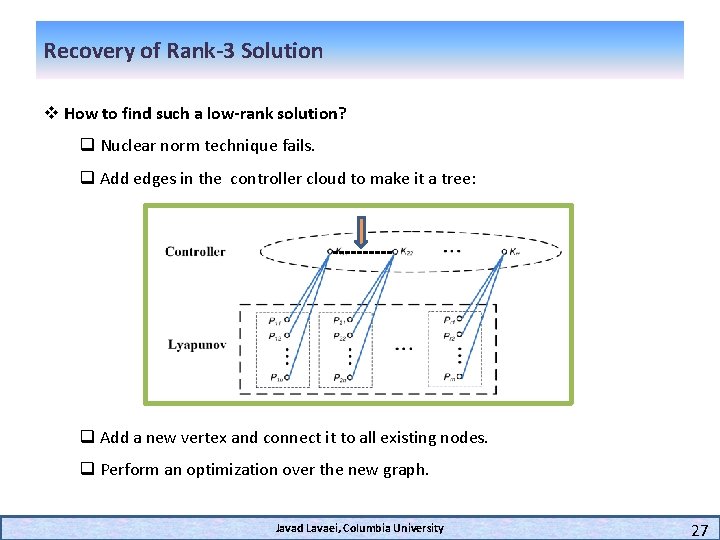
Recovery of Rank-3 Solution v How to find such a low-rank solution? q Nuclear norm technique fails. q Add edges in the controller cloud to make it a tree: q Add a new vertex and connect it to all existing nodes. q Perform an optimization over the new graph. Javad Lavaei, Columbia University 27

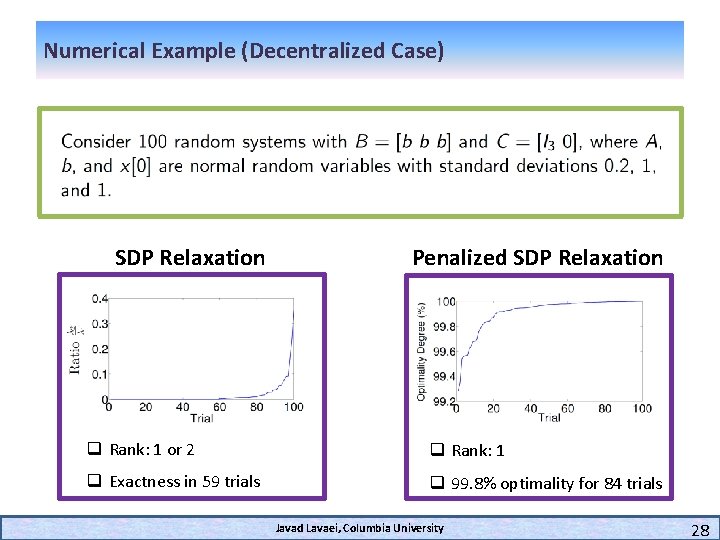
Numerical Example (Decentralized Case) SDP Relaxation Penalized SDP Relaxation q Rank: 1 or 2 q Rank: 1 q Exactness in 59 trials q 99. 8% optimality for 84 trials Javad Lavaei, Columbia University 28

Distributed Case v 100 random systems with standard deviation 3 for A and B, and 2 for X 0. v Each communication link exists with probability 0. 9. Javad Lavaei, Columbia University 29

Outline v Convex relaxation for highly structured optimization (Joint work with: Somayeh Sojoudi) v Optimization over power networks (Joint work with: Steven Low, David Tse, Stephen Boyd, Somayeh Sojoudi, Ramtin Madani, Baosen Zhang, Matt Kraning, Eric Chu) v Optimal decentralized control (Joint work with: Ghazal Fazelnia and Ramtin Madani) v General theory for polynomial optimization (Joint work with: Ramtin Madani, Somayeh Sojoudi, and Ghazal Fazelnia) Javad Lavaei, Columbia University 29

Polynomial Optimization v Consider an arbitrary polynomial optimization: v Fact 1: v Fact 2: Javad Lavaei, Columbia University 31

Polynomial Optimization q Technique: distributed computation q This gives rise to a sparse QCQP with a sparse graph. q Question: Given a sparse LMI, find a low-rank solution in polynomial time? q We have a theory for relating the rank of W to the topology of its graph. Javad Lavaei, Columbia University 32

Conclusions v Convex relaxation for highly structured optimization: q Complexity of SDP relaxation can be related to properties of a generalized graph. v Optimization over power networks: q Optimization over power networks becomes mostly easy due to their structures. v Optimal decentralized control: q ODC is a highly sparse nonlinear optimization so its relaxation has a rank 1 -3 solution. v General theory for polynomial optimization: q Every polynomial optimization has an SDP relaxation with a rank 1 -3 solution. Javad Lavaei, Columbia University 33