Convex hulls Quickhull Quicksort The Quickhull algorithm is

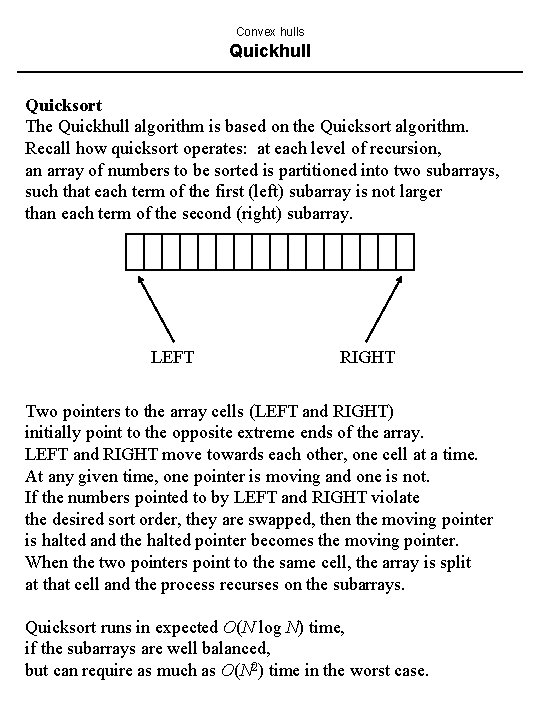
Convex hulls Quickhull Quicksort The Quickhull algorithm is based on the Quicksort algorithm. Recall how quicksort operates: at each level of recursion, an array of numbers to be sorted is partitioned into two subarrays, such that each term of the first (left) subarray is not larger than each term of the second (right) subarray. LEFT RIGHT Two pointers to the array cells (LEFT and RIGHT) initially point to the opposite extreme ends of the array. LEFT and RIGHT move towards each other, one cell at a time. At any given time, one pointer is moving and one is not. If the numbers pointed to by LEFT and RIGHT violate the desired sort order, they are swapped, then the moving pointer is halted and the halted pointer becomes the moving pointer. When the two pointers point to the same cell, the array is split at that cell and the process recurses on the subarrays. Quicksort runs in expected O(N log N) time, if the subarrays are well balanced, but can require as much as O(N 2) time in the worst case.

Convex hulls Quickhull overview Quickhull operates in a similar manner. It recursively partitions the point set S, so as to find the convex hull for each subset. The hull at each level of the recursion is formed by concatenating the hulls found at the next level down. S

Convex hulls Quickhull Initial partition The initial partition of S is determined by a line L through the points l, r S with the smallest and largest absciss S(1) S is the subset of S on or above L. S(2) S is the subset of S on or below L. Note that {S(1), S(2)} is not a strict partition of S, as S(1) S(2) {l, r}. This is not a difficulty. The idea now is to construct hulls H(S(1)) and H(S(2)), then concatenate them to get H(S). The process is the same for S(1) and S(2), we consider S(1) r S(2) l L

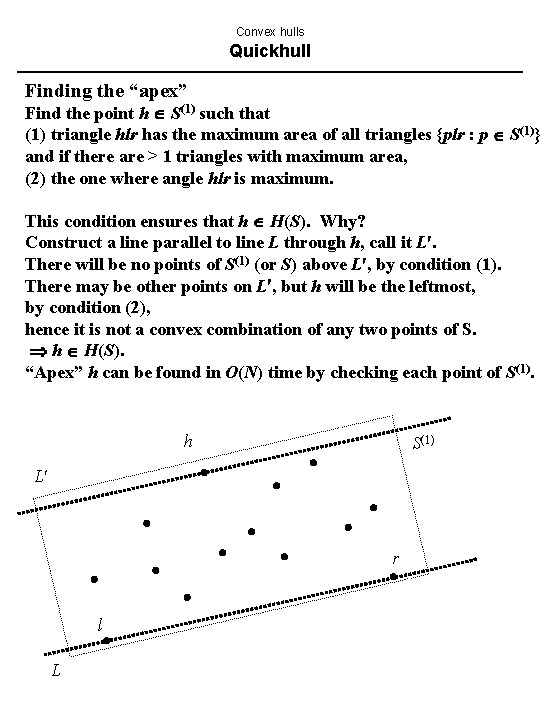
Convex hulls Quickhull Finding the “apex” Find the point h S(1) such that (1) triangle hlr has the maximum area of all triangles {plr : p S(1)} and if there are > 1 triangles with maximum area, (2) the one where angle hlr is maximum. This condition ensures that h H(S). Why? Construct a line parallel to line L through h, call it L. There will be no points of S(1) (or S) above L , by condition (1). There may be other points on L , but h will be the leftmost, by condition (2), hence it is not a convex combination of any two points of S. h H(S). “Apex” h can be found in O(N) time by checking each point of S(1). h S(1) L r l L

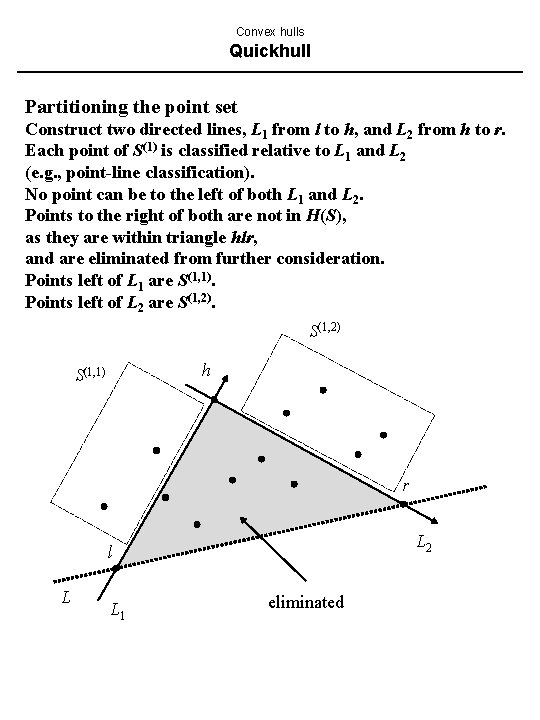
Convex hulls Quickhull Partitioning the point set Construct two directed lines, L 1 from l to h, and L 2 from h to r. Each point of S(1) is classified relative to L 1 and L 2 (e. g. , point-line classification). No point can be to the left of both L 1 and L 2. Points to the right of both are not in H(S), as they are within triangle hlr, and are eliminated from further consideration. Points left of L 1 are S(1, 1). Points left of L 2 are S(1, 2) h S(1, 1) r L 2 l L L 1 eliminated

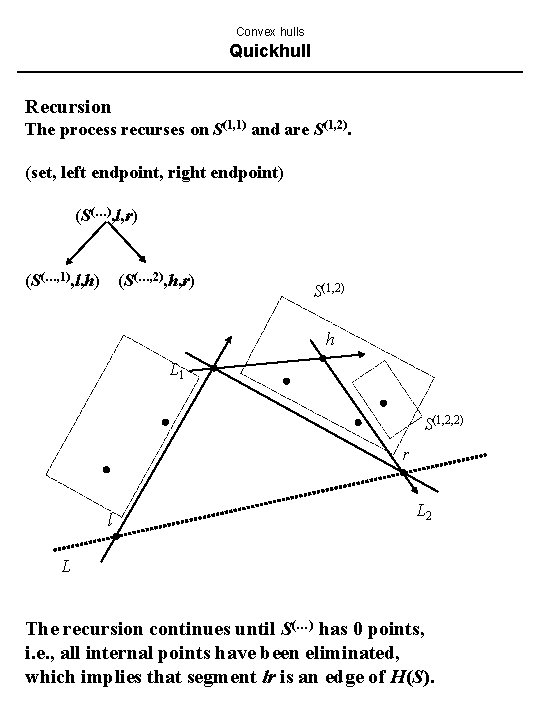
Convex hulls Quickhull Recursion The process recurses on S(1, 1) and are S(1, 2). (set, left endpoint, right endpoint) (S(…), l, r) (S(…, 1), l, h) (S(…, 2), h, r) S(1, 2) h L 1 S(1, 2, 2) r l L 2 L The recursion continues until S(…) has 0 points, i. e. , all internal points have been eliminated, which implies that segment lr is an edge of H(S).

Convex hulls Quickhull Geometric primitives The geometric primitives used by this algorithm are: 1. Point-line classification 2. Area of a triangle Both of these require O(1) time.

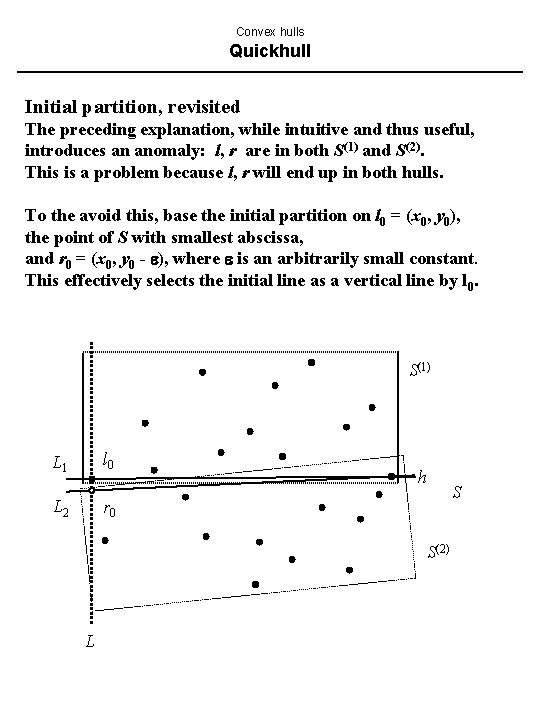
Convex hulls Quickhull Initial partition, revisited The preceding explanation, while intuitive and thus useful, introduces an anomaly: l, r are in both S(1) and S(2). This is a problem because l, r will end up in both hulls. To the avoid this, base the initial partition on l 0 = (x 0, y 0), the point of S with smallest abscissa, and r 0 = (x 0, y 0 - ), where is an arbitrarily small constant. This effectively selects the initial line as a vertical line by l 0. S(1) l 0 L 1 L 2 h S r 0 S(2) L

Convex hulls Quickhull General function S is assumed to have at least 2 elements (the recursion ends otherwise). FURTHEST(S, l, r) is a function, not given here, that finds the apex point h as previously defined. The operator || denotes list concatentation. Procedure QUICKHULL returns an ordered list of points. 1 2 3 4 5 6 7 8 9 procedure QUICKHULL(S, l, r) begin if S = {l, r} then return (l, r) /* lr is an edge of H(S) */ else h = FURTHEST(S, l, r) S(1) = p S p is on or left of line lh S(2) = p S p is on or left of line hr return QUICKHULL(S(1), l, h) || (QUICKHULL(S(2), h, r) - h) 10 end 11 end Initial call 1 begin 2 l 0 = (x 0, y 0) /* point of S with smallest abscissa */ 3 r 0 = (x 0, y 0 - ) 4 result = QUICKHULL(S, l 0, r 0) - r 0 /* The point r 0 is eliminated from the final list*/ 5 end

Convex hulls Quickhull Analysis Worst case time: O(N 2) Expected time: O(N log N) Storage: O(N 2) At each level of the recursion, partitioning S into S(1) and S(2) requires O(N) time. If S(1) and S(2) were guaranteed to have a size equal to a fixed portion of S, and this held at each level the worst case time would be O(N log N). However, those criteria do not apply; S(1) and S(2) may have size in O(N) (they are not balanced). Hence the worst case time is O(N 2), O(N) at each of O(N) levels of recursion. The same applies to storage.

Convex hulls Divide-and-conquer design goal QUICKHULL recursively subdivides point set S, and assembles the convex hull H(S) by “merging” the subproblem results. Advantages: 1. Subdivision allows parallelization 2. Merge process is very simple (concatenation) Disadvantage: 1. Inability to control or guarantee subproblem size results in suboptimum worst case time performance. We seek a divide-and-conquer algorithm which divides the problem into subproblems of approximately equal size.

Convex hulls Divide-and-conquer Union of convex hulls, 1 Suppose we have S and want to compute H(S). Further suppose S has been partitioned into S 1 and S 2, each containing half the points of S. If H(S 1) and H(S 2) are found separately (recursively), how much additional work is required to compute H(S 1 S 2), i. e. , H(S)? In other words, is it easier to find H(S) = H(S 1 S 2) given H(S 1) and H(S 2) than to find H(S) directly? To do so, we use the relation: H(S 1 S 2) = H(H(S 1) H(S 2)) The convex hull of the union of the two subsets is the same as the convex hull of the union of the convex hulls of the two subsets.

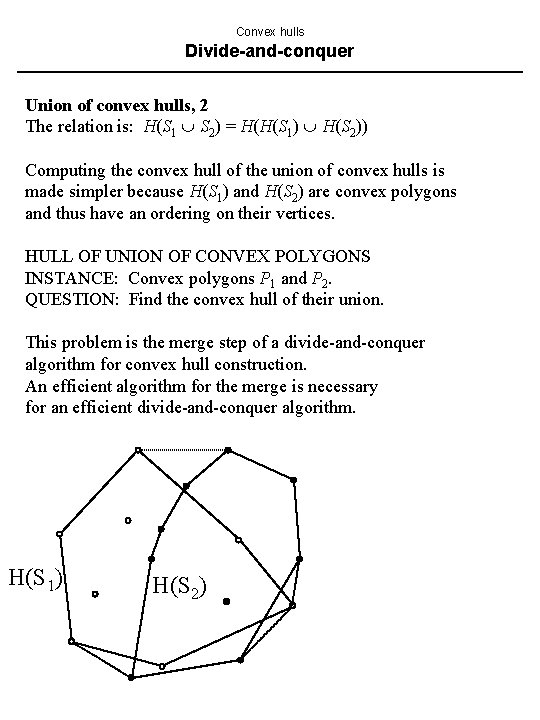
Convex hulls Divide-and-conquer Union of convex hulls, 2 The relation is: H(S 1 S 2) = H(H(S 1) H(S 2)) Computing the convex hull of the union of convex hulls is made simpler because H(S 1) and H(S 2) are convex polygons and thus have an ordering on their vertices. HULL OF UNION OF CONVEX POLYGONS INSTANCE: Convex polygons P 1 and P 2. QUESTION: Find the convex hull of their union. This problem is the merge step of a divide-and-conquer algorithm for convex hull construction. An efficient algorithm for the merge is necessary for an efficient divide-and-conquer algorithm. H(S 1) H(S 2)

Convex hulls Divide-and-conquer Overview of divide-and-conquer algorithm 1. If |S| k 0 (k 0 is a small integer), construct the convex hull directly by some method and stop, else go to step 2. (For example, for k 0 = 3 the hull is a triangle, O(1). ) 2. Partition the set S arbitrarily into two subsets S 1 and S 2 of approximately equal sizes. 3. Recursively find the convex hulls H(S 1) and H(S 2). 4. Merge the two hulls together to form H(S). Let U(N) denote the time needed to find the hull of the union of two convex polygons (convex hulls), each with N/2 vertices. Let T(N) is the time required to find the convex hull of N points. T(N) 2 T(N/2) + U(N) total time subproblem time merge time If U(N) O(N), then T(N) O(N log N) (by recurrence relation), so we seek an O(N) merge algorithm, i. e. an O(N) convex polygon union algorithm.

Convex hulls Divide-and-conquer Merge algorithm, 1 This procedure finds the convex hull of the union of two convex polygons P 1 and P 2. 1. Find a point p that is internal to P 1 (e. g. centroid). Note that this point p will be internal to H(P 1 P 2). 2. Determine whether or not p is internal to P 2. This can be done in O(N) time (convex polygon inclusion). If p is not internal to P 2, go to step 4. 3. Point p is internal to P 2. The vertices of both P 1 and P 2 occur in sorted angular order about p. Merge the lists of vertices in O(N) time to obtain a sorted list of the vertices of both P 1 and P 2. Go to step 5. P 1 P 2 p

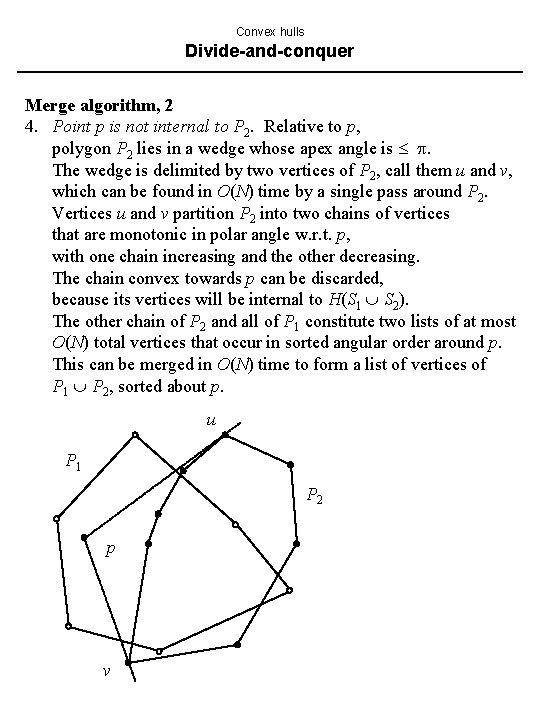
Convex hulls Divide-and-conquer Merge algorithm, 2 4. Point p is not internal to P 2. Relative to p, polygon P 2 lies in a wedge whose apex angle is . The wedge is delimited by two vertices of P 2, call them u and v, which can be found in O(N) time by a single pass around P 2. Vertices u and v partition P 2 into two chains of vertices that are monotonic in polar angle w. r. t. p, with one chain increasing and the other decreasing. The chain convex towards p can be discarded, because its vertices will be internal to H(S 1 S 2). The other chain of P 2 and all of P 1 constitute two lists of at most O(N) total vertices that occur in sorted angular order around p. This can be merged in O(N) time to form a list of vertices of P 1 P 2, sorted about p. u P 1 P 2 p v

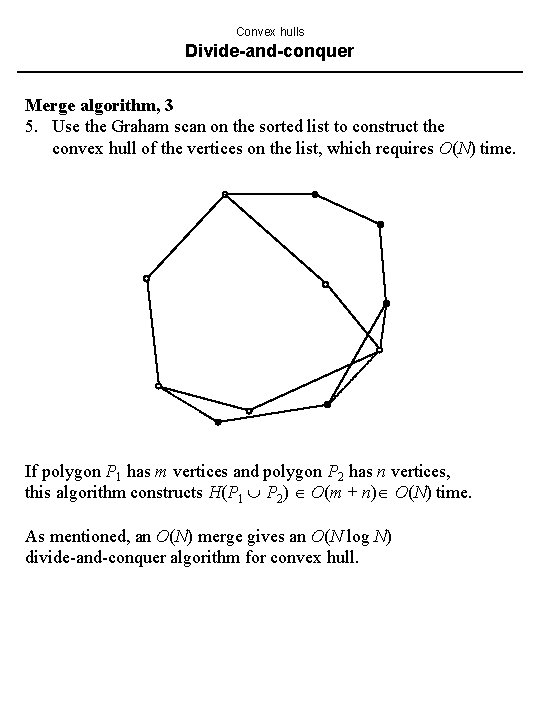
Convex hulls Divide-and-conquer Merge algorithm, 3 5. Use the Graham scan on the sorted list to construct the convex hull of the vertices on the list, which requires O(N) time. If polygon P 1 has m vertices and polygon P 2 has n vertices, this algorithm constructs H(P 1 P 2) O(m + n) O(N) time. As mentioned, an O(N) merge gives an O(N log N) divide-and-conquer algorithm for convex hull.

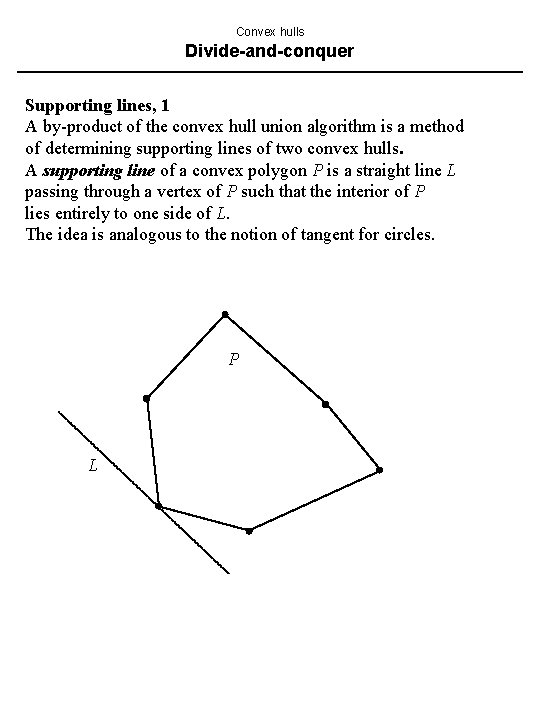
Convex hulls Divide-and-conquer Supporting lines, 1 A by-product of the convex hull union algorithm is a method of determining supporting lines of two convex hulls. A supporting line of a convex polygon P is a straight line L passing through a vertex of P such that the interior of P lies entirely to one side of L. The idea is analogous to the notion of tangent for circles. P L

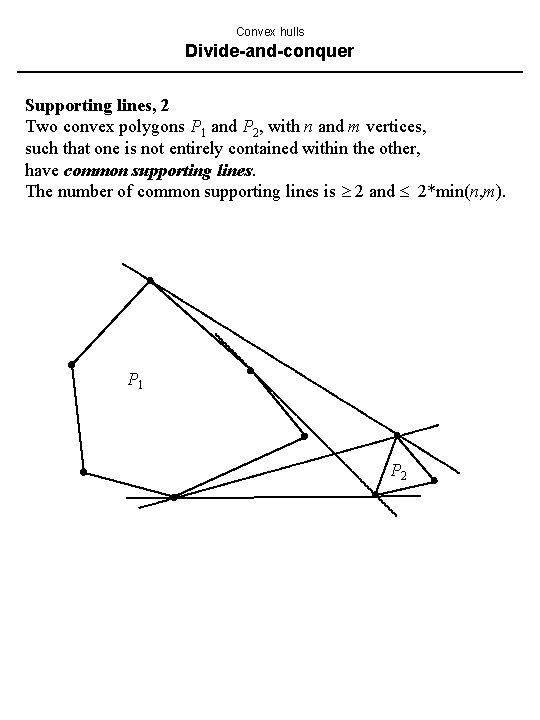
Convex hulls Divide-and-conquer Supporting lines, 2 Two convex polygons P 1 and P 2, with n and m vertices, such that one is not entirely contained within the other, have common supporting lines. The number of common supporting lines is 2 and 2*min(n, m). P 1 P 2

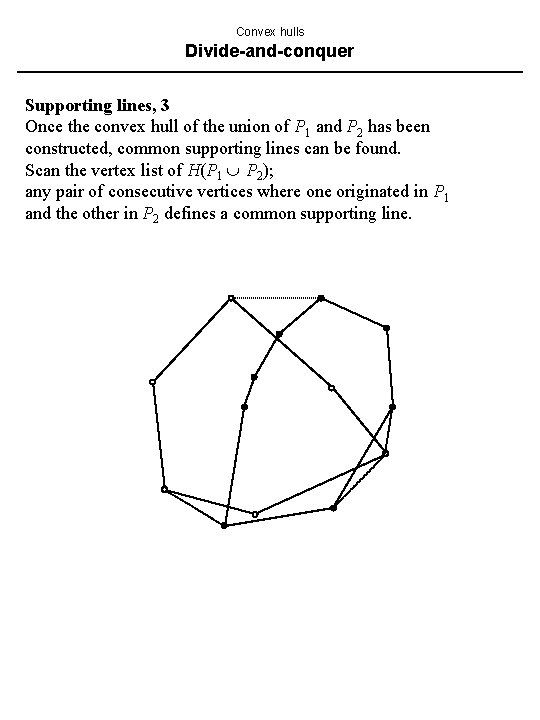
Convex hulls Divide-and-conquer Supporting lines, 3 Once the convex hull of the union of P 1 and P 2 has been constructed, common supporting lines can be found. Scan the vertex list of H(P 1 P 2); any pair of consecutive vertices where one originated in P 1 and the other in P 2 defines a common supporting line.