Convergence of Fourier series It is known that

Convergence of Fourier series It is known that a periodic signal x(t) has a Fourier series representation if it satisfies the following Dirichlet conditions: • x(t) is absolutely integrable over any period, that is, • x(t) has a finite number of maxima and minima within any finite interval of t. • x(t) has a finite number of discontinuities within any finite interval of t, and each of these discontinuities is finite. Signals and systems analysis 1 ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ

Convergence of Fourier series • Dirichlet conditions are sufficient but not necessary. we can have examples of Fourier series for functions that violate some of the Dirichlet conditions. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 2

Fourier series properties • Linearity: • Let F denote the transformation from f(t) to the Fourier coefficients. F is a linear transformation. • If F f(t) = cn and F g(t) = dn. Then • and Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 3

Fourier series properties • Time Shifting: • Shifting in time equals a phase shift of Fourier coefficients. • Remark: The magnitudes of the Fourier series coefficients are not changed, only their phases. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 4

Fourier series properties • Frequency shifting: • The spectrum of a signal, x(t), can be shifted by multiplying the signal by a complex exponential, , where k 0 is an integer and ω0 is the fundamental frequency. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 5

Fourier series properties • Time scaling: • Time scaling applied on a periodic signal changes the fundamental frequency of the signal. • For example, f(at) has fundamental frequency aw 0 and fundamental period a– 1 T. The Fourier series coefficients do not change: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 6

Fourier series properties • Time reversal: • Time reversal leads to a “sequence reversal” of the corresponding sequence of Fourier series coefficients: Interesting consequences are that • For f(t) even, the sequence of coefficients is also even (c-n= cn). • For f(t) odd, the sequence of coefficients is also odd (c-n= -cn). Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 7

Fourier series properties • Multiplication of two signals: • Suppose that x(t) and y(t) are both periodic with period T. Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 8

Fourier series properties • Differentiation in Fourier domain: • The derivative of is. Therefore, if the FS spectrum for a time-domain function f(t) is cn, then the FS spectrum for its derivative is jnω0 cn, where ω0 is the fundamental frequency. Note that the FS coefficient with k = 0 is zero, as the dc component is lost in differentiating a signal. In general, Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 9

Fourier series properties • Integration in Fourier domain: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 10

Fourier series properties • Conjugation & conjugate symmetry: Taking the conjugate of a periodic signal has the effect of conjugation and index reversal on the spectral coefficients: Interesting consequences are that: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 11

Fourier series properties • For x(t) real, and the sequence of coefficients is conjugate symmetric; that is, This implies (magnitude is even), (phase is odd). Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 12

Fourier series properties • For x(t) real and even, the sequence of coefficients is also real and even ( ). • For x(t) real and odd, the sequence of coefficients is imaginary and odd ( purely imaginary). Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 13

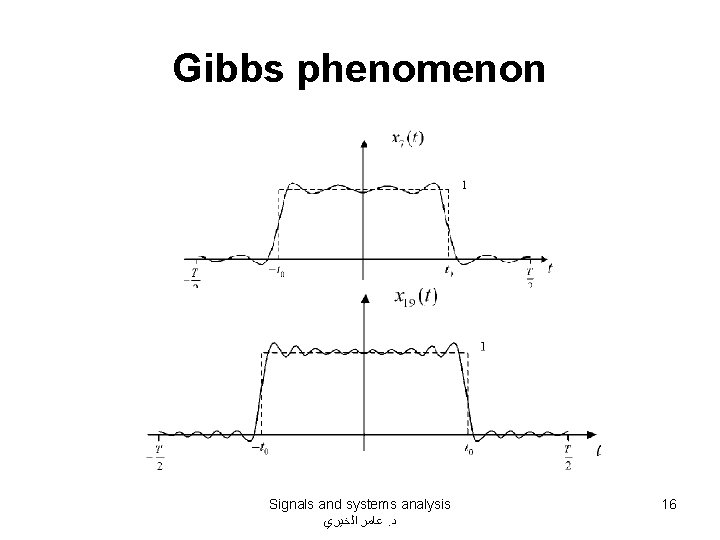
Gibbs phenomenon • An interesting observation can be made when one looks at the graph of a truncated Fourier series of a square wave. • The graph over one period looks like: Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 14

Gibbs phenomenon • We can see that there are ripples of a certain amplitude in the approximation, especially close to the discontinuities in the signal. The surprising thing is that the peak amplitude of these ripples does not diminish when we add more terms in the truncated Fourier series. For example, for N=19 in the Figure shown in the next slide; the approximation gets closer to a square wave, but we can still see rather large, but narrow, ripples around the discontinuities. • This is called the Gibbs phenomenon Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 15

Gibbs phenomenon Signals and systems analysis ﻋﺎﻣﺮ ﺍﻟﺨﻴﺮﻱ. ﺩ 16