CONTROLLER DESIGN OBJECTIVE Type of compensator Design of

CONTROLLER DESIGN OBJECTIVE ~ Type of compensator ~ Design of compensator in time response ~ Design of compensator in frequency response

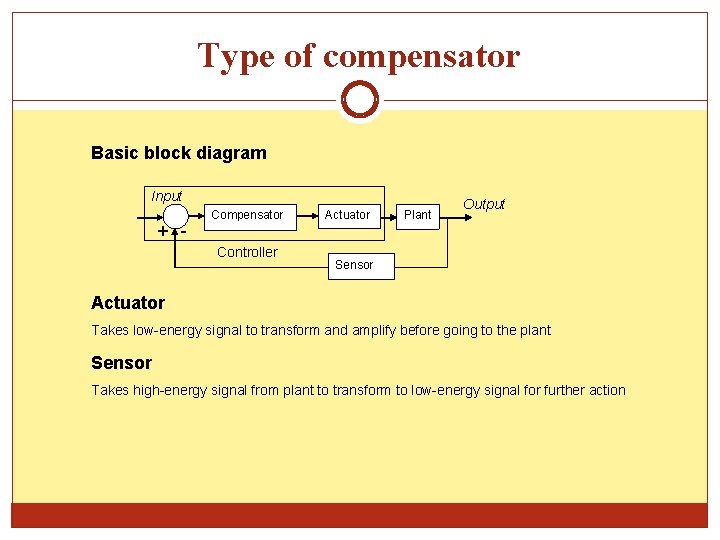
Type of compensator Basic block diagram Input + - Compensator Controller Actuator Plant Output Sensor Actuator Takes low-energy signal to transform and amplify before going to the plant Sensor Takes high-energy signal from plant to transform to low-energy signal for further action

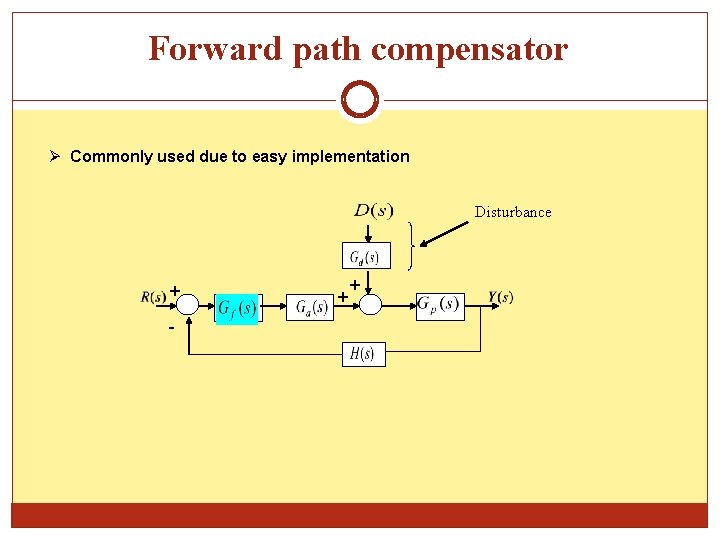
Forward path compensator Commonly used due to easy implementation Disturbance + - + +

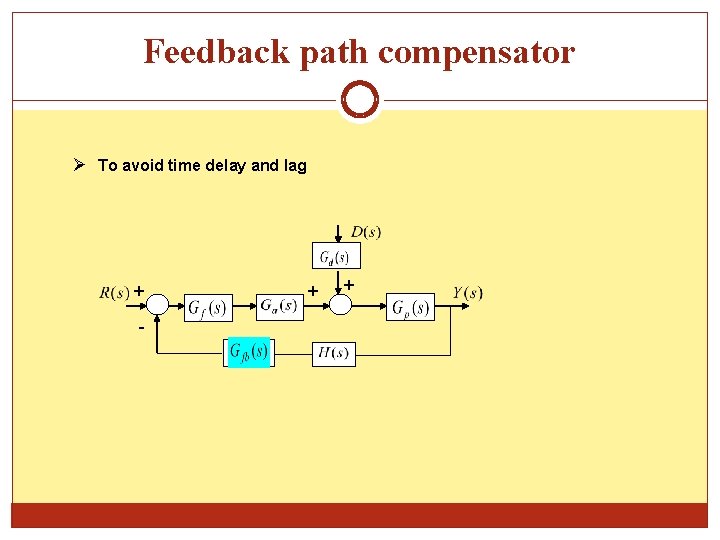
Feedback path compensator To avoid time delay and lag + - + +

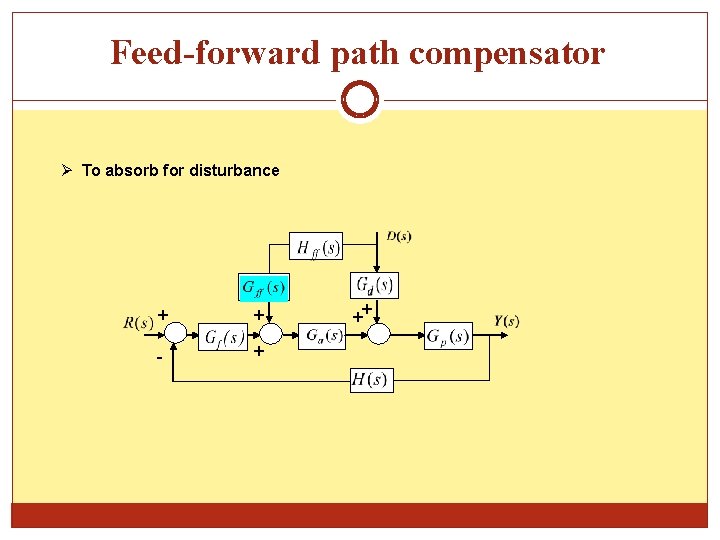
Feed-forward path compensator To absorb for disturbance + + - + ++

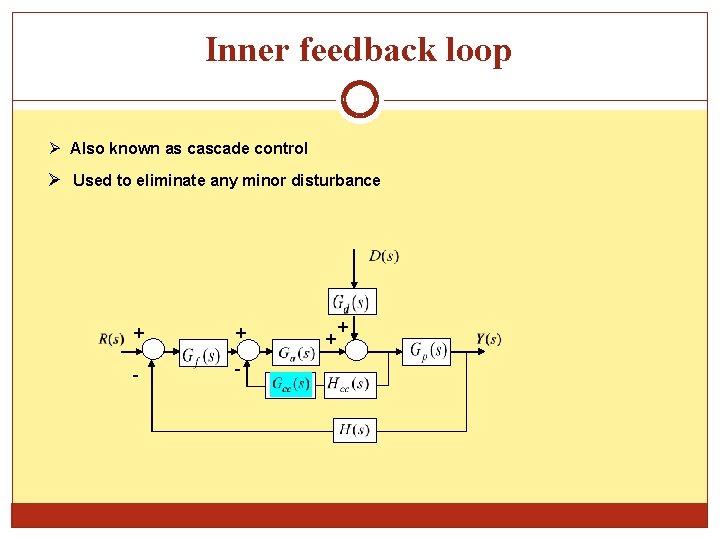
Inner feedback loop Also known as cascade control Used to eliminate any minor disturbance + + - - + +

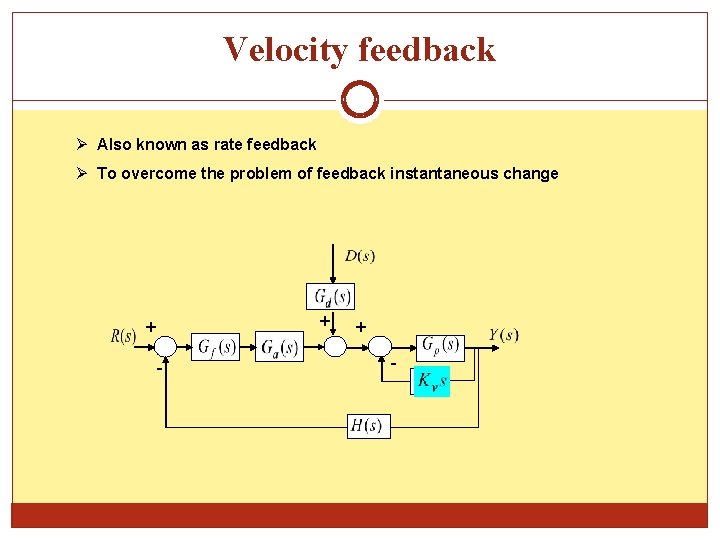
Velocity feedback Also known as rate feedback To overcome the problem of feedback instantaneous change + + -

Selection of compensator (1) Flow • Very noisy, thus need derivative-action (D) • Overall gain less than, integral-action will ensure no steady-state error. (I) (2) Level • Normally is of type 1, thus just required proportional-action. (P) (3) Temperature • Thermal delay, thus normally required PID-action (4) Pressure • Characteristic can be fast or slow depending on application, thus required PI or P.

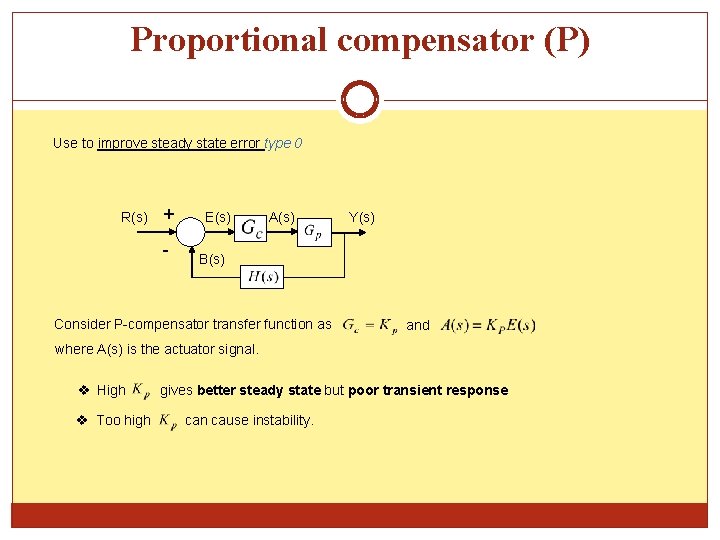
Proportional compensator (P) Use to improve steady state error type 0 R(s) + - E(s) A(s) Y(s) B(s) Consider P-compensator transfer function as and where A(s) is the actuator signal. v High gives better steady state but poor transient response v Too high can cause instability.

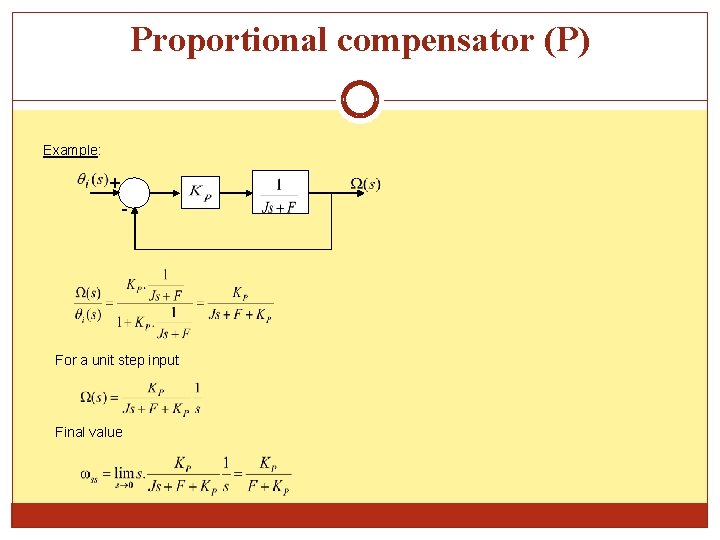
Proportional compensator (P) Example: + - For a unit step input Final value

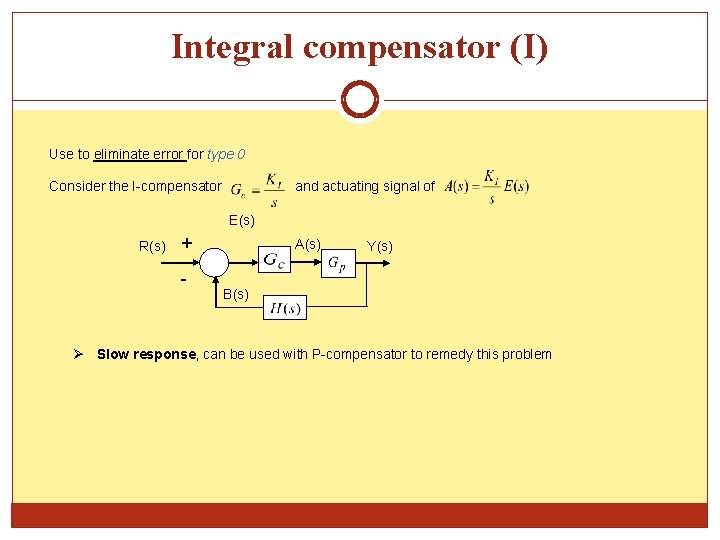
Integral compensator (I) Use to eliminate error for type 0 Consider the I-compensator and actuating signal of E(s) R(s) + - A(s) Y(s) B(s) Slow response, can be used with P-compensator to remedy this problem

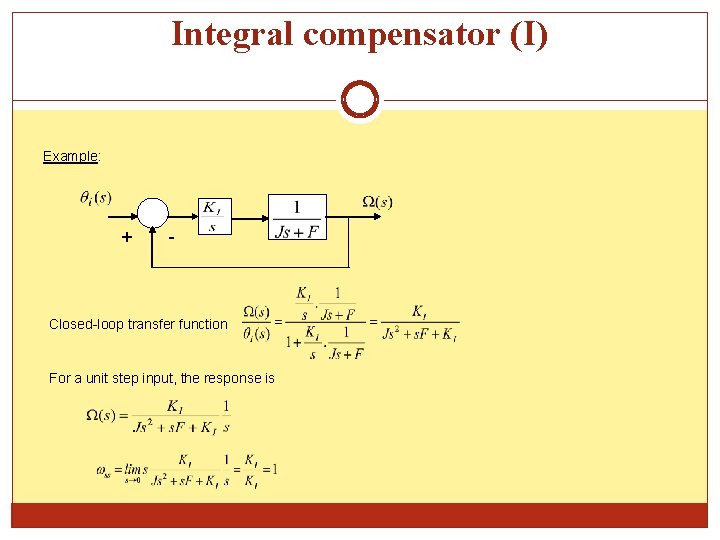
Integral compensator (I) Example: + - Closed-loop transfer function For a unit step input, the response is

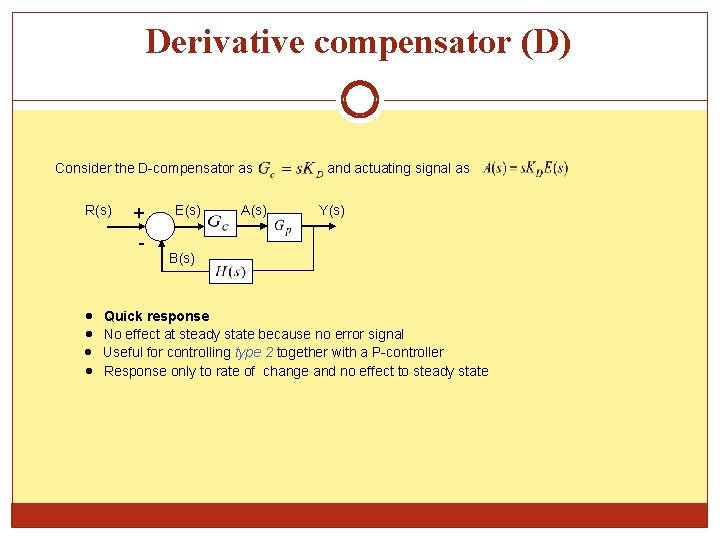
Derivative compensator (D) Consider the D-compensator as R(s) + - E(s) A(s) and actuating signal as Y(s) B(s) Quick response No effect at steady state because no error signal Useful for controlling type 2 together with a P-controller Response only to rate of change and no effect to steady state

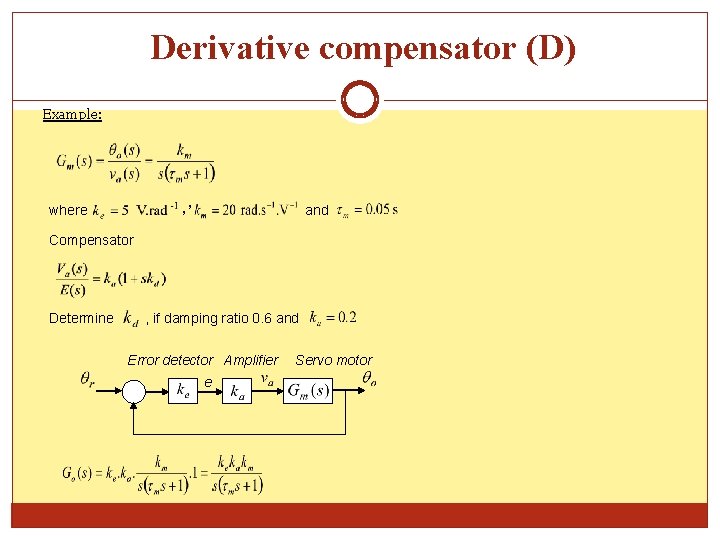
Derivative compensator (D) Example: , , where and Compensator Determine , if damping ratio 0. 6 and Error detector Amplifier e Servo motor

Derivative compensator (D) New open loop transfer function Give closed loop For , C. f. nominal second order Hence , , and

The characteristics of P, I and D compensators A proportional controller (Kp) will have the effect of reducing the rise time and will reduce , but never eliminate, the steady-state error. An integral control (Ki) will have the effect of eliminating the steady-state error, but it may make the transient response worse. A derivative control (Kd) will have the effect of increasing the stability of the system, reducing the overshoot, and improving the transient response. Effects of each of controllers Kp, Kd, and Ki on a closed-loop system are summarized in the table shown below.

Proportional-integral compensator (PI) Use for combination of fast convergence zero steady state error or

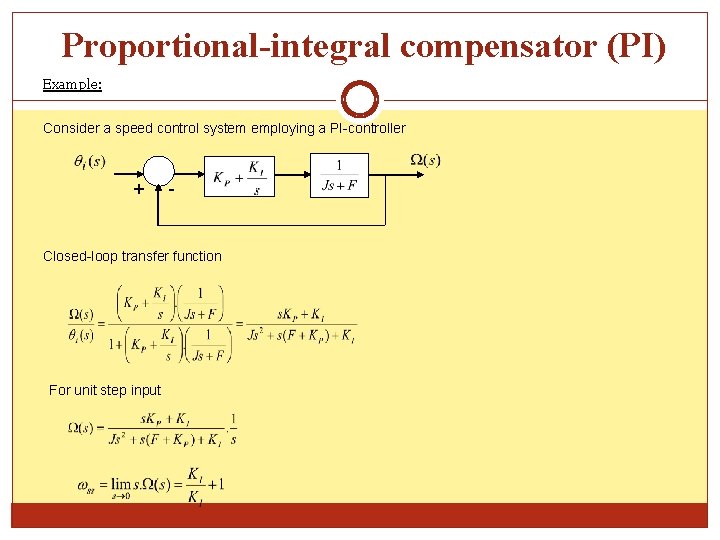
Proportional-integral compensator (PI) Example: Consider a speed control system employing a PI-controller + - Closed-loop transfer function For unit step input

Proportional-integral-derivative compensator (PID) or

PID Tuning q There are many techniques for tuning PID

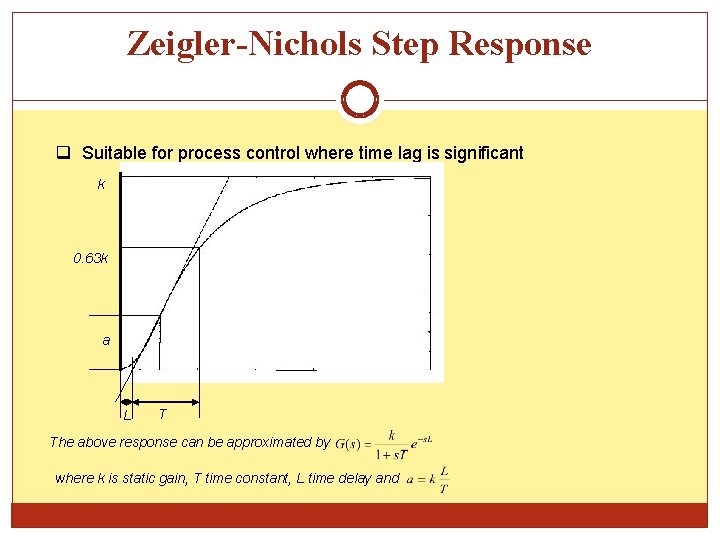
Zeigler-Nichols Step Response q Suitable for process control where time lag is significant k 0. 63 k a L T The above response can be approximated by where k is static gain, T time constant, L time delay and

Zeigler-Nichols Step Response Based rule-of-thumb, for the controller gains can be approximated by Controller PID PI P 1/a 0. 9/a 1. 2/a 3 L 2 L L/2

Zeigler-Nichols Closed-Loop Method q Using Routh-Hurwitz criteria, we can determined the marginally stable’s gain, and its period of oscillation, for a controller with a gain of K q With rule-of-thumb: Controller PID PI P 0. 833 T 0. 5 T 0. 125 T

Zeigler-Nichols Closed-Loop Method Example Design a P, PI and PID controller for a plant with an open loop transfer function as follows With a gain of K connected in cascade to the system, its characteristic equation becomes Forming the Routh array 1 11 6 6(1+K) 1+K

Zeigler-Nichols Closed-Loop Method Thus and its frequency of oscillation which gives T= 1. 895 s This gives Controller P 6 PI 4. 5 0. 947 PID 5 1. 57 Their step response are 0. 237

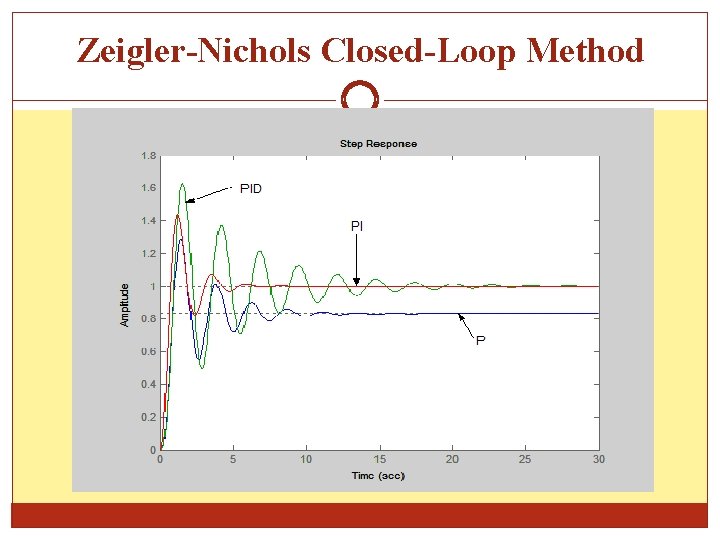
Zeigler-Nichols Closed-Loop Method

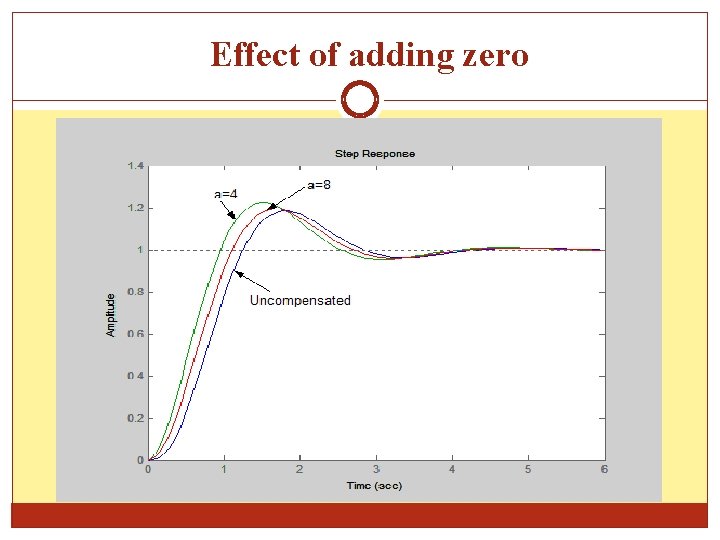
Effect of adding zero Example Consider an open-loop transfer function By introducing a zero and normalizing the response The step response for uncompensated, a=4 and a=8 are shown in following figure: see behind….

Effect of adding zero

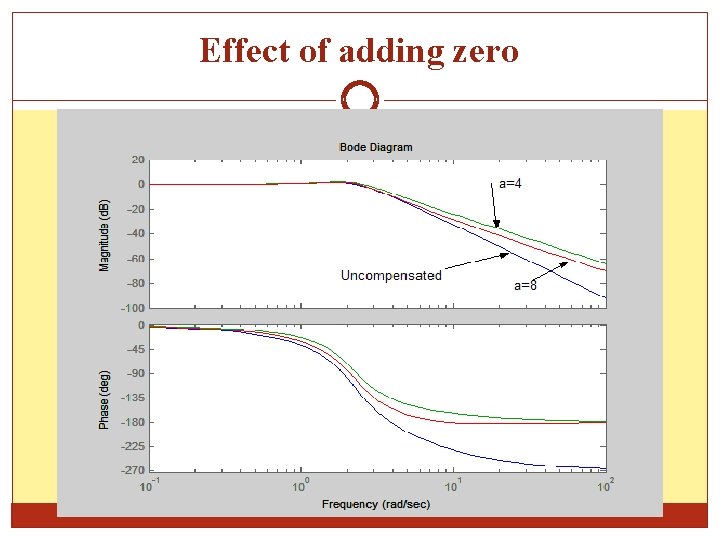
Effect of adding zero

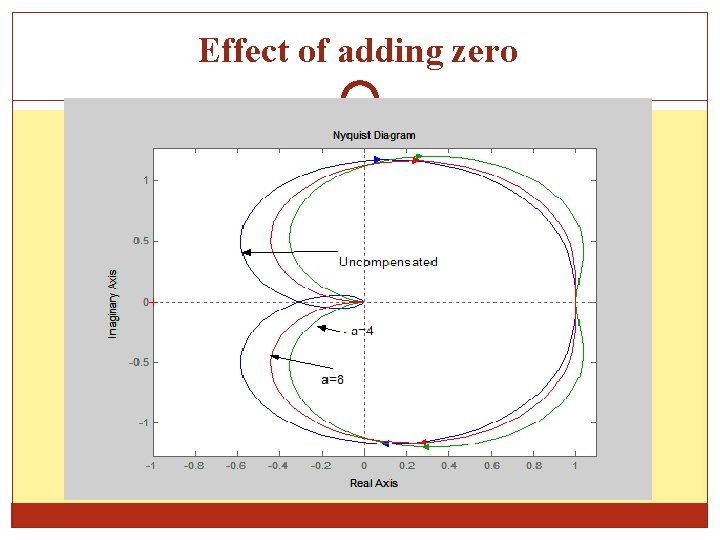
Effect of adding zero

Effect of adding zero As a conclusion, the effect of introducing zero are: Reduce rise time, peak time Increases overshoot As the zero approach the origin its contribution is more significant Bandwidth increase Improve gain margin

Effect of adding pole For a compensator with a pole and normalizing the output The step response for uncompensated, a=4 and a=8 are shown in the following figure: see behind….

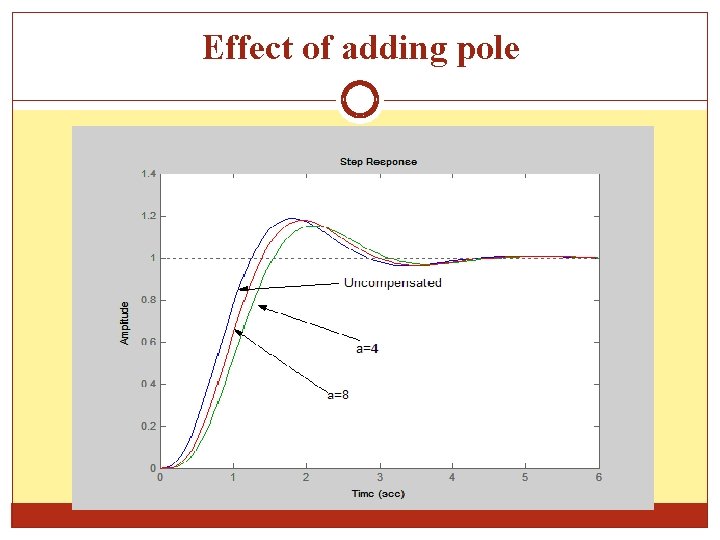
Effect of adding pole

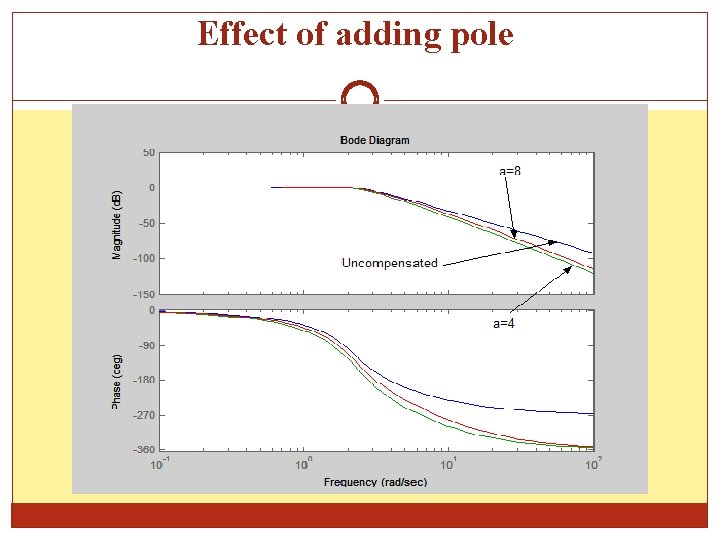
Effect of adding pole

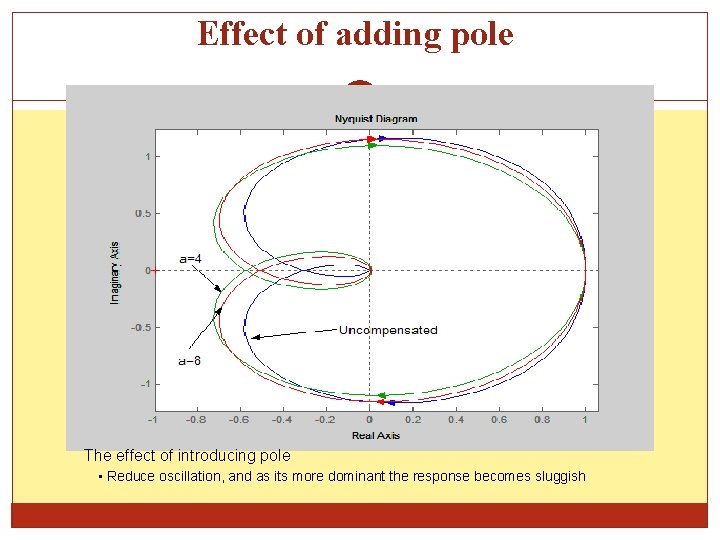
Effect of adding pole The effect of introducing pole • Reduce oscillation, and as its more dominant the response becomes sluggish

Design in time response…

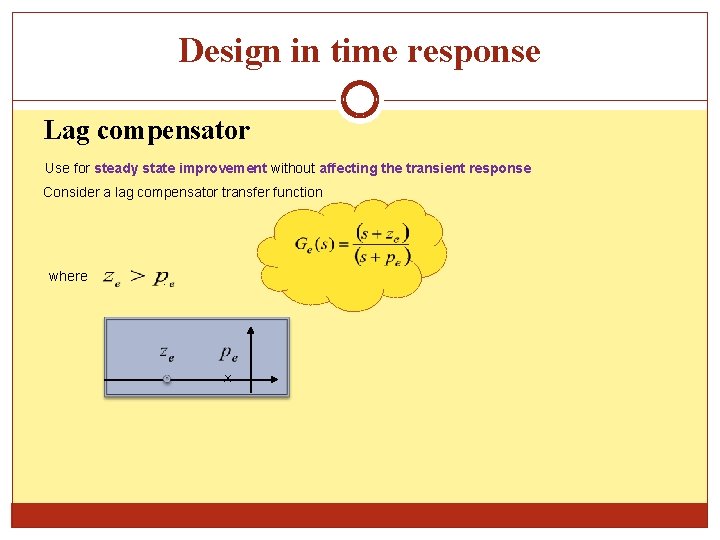
Design in time response Lag compensator Use for steady state improvement without affecting the transient response Consider a lag compensator transfer function where .

Design in time response Consider a plant Dc gain without compensator where and zeros and poles position from test point. With compensator As , thus with that the steady state error is reduced.

Design in time response Lead compensator For transient response where Uncompensated Compensated Thus .

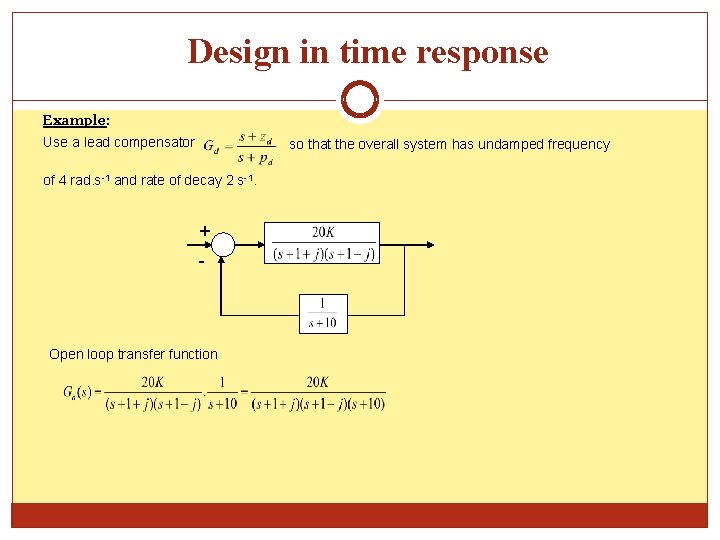
Design in time response Example: Use a lead compensator of 4 rad. s-1 and rate of decay 2 s-1. + - Open loop transfer function so that the overall system has undamped frequency

Design in time response Dominant poles and that give a damping ratio of The test point for specification:

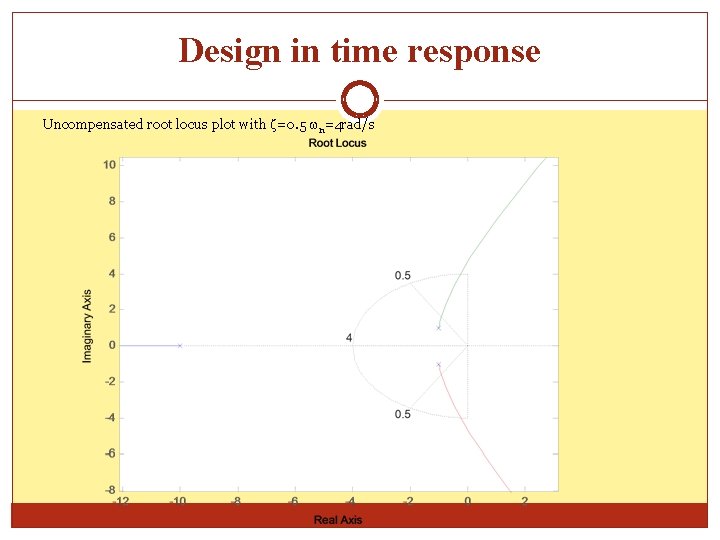
Design in time response Uncompensated root locus plot with =0. 5 n=4 rad/s

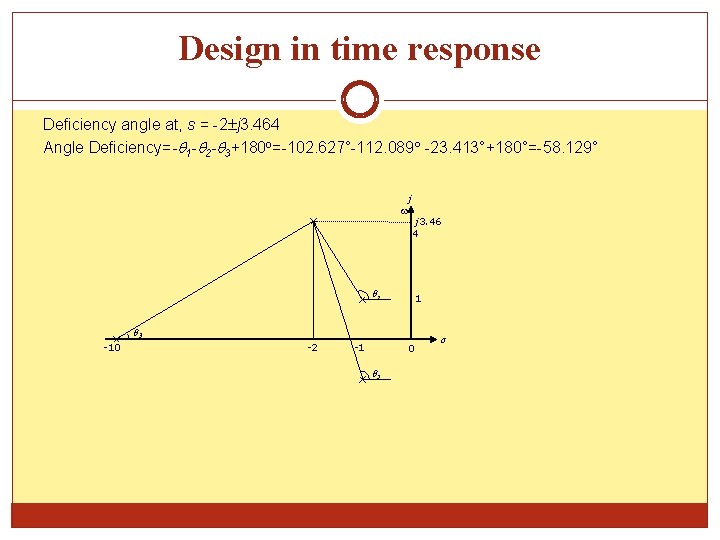
Design in time response Deficiency angle at, s = -2 j 3. 464 Angle Deficiency=- 1 - 2 - 3+180 o=-102. 627°-112. 089 -23. 413°+180°=-58. 129° j j 3. 46 4 1 1 3 -10 -2 -1 0 2 σ

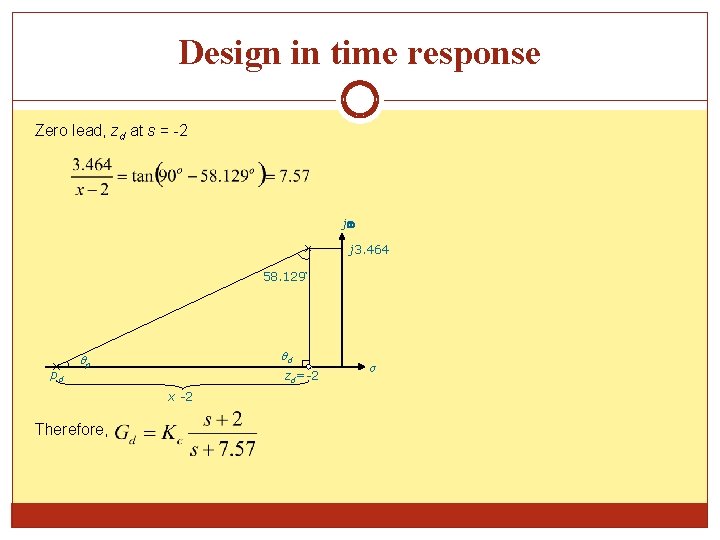
Design in time response Zero lead, zd at s = -2 j j 3. 464 58. 129 pd d p zd=-2 x -2 Therefore, σ

Design in time response Hence, the dc gain Rearrange the equation (after convert to polar form) Which give the OPEN loop transfer function

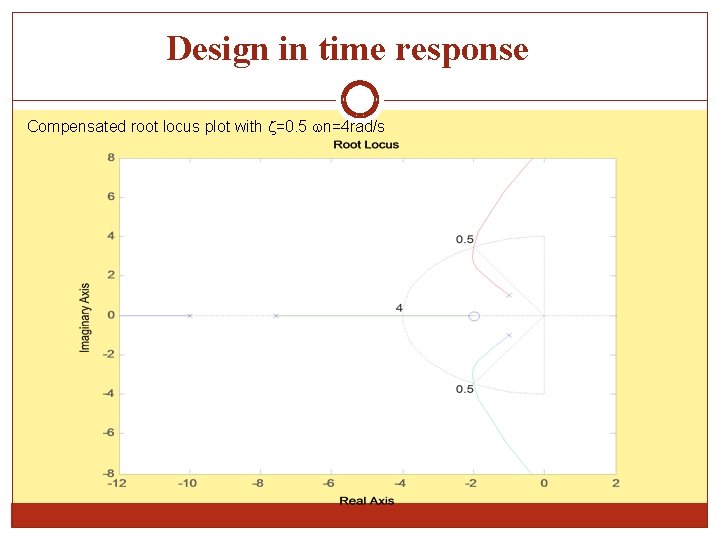
Design in time response Compensated root locus plot with =0. 5 n=4 rad/s

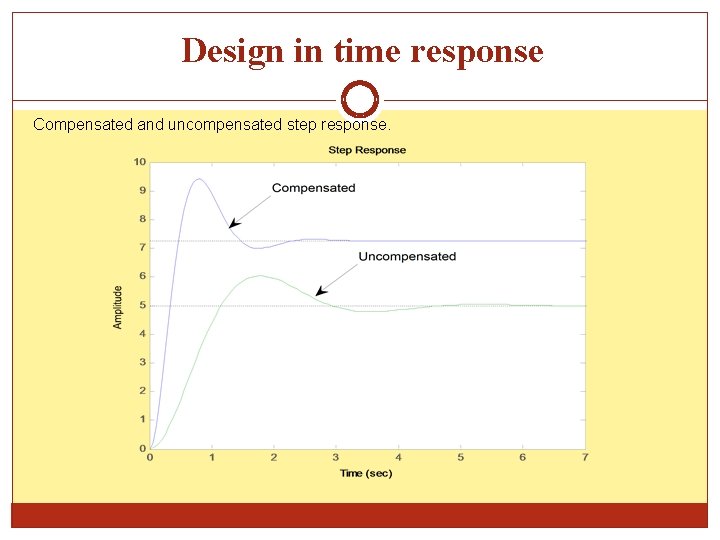
Design in time response Compensated and uncompensated step response.

Design in frequency response…

Design in frequency response Basic concepts in the design criteria Increase of PHASE MARGIN, the overshoot will be reduced Increase of BANDWIDTH, the response will be faster Increase of LOW FREQUENCY MAGNITUDE, the steady state will be reduced ## The bandwidth is the frequency where the magnitude has dropped to 1/√ 2 of its value at ω = 0

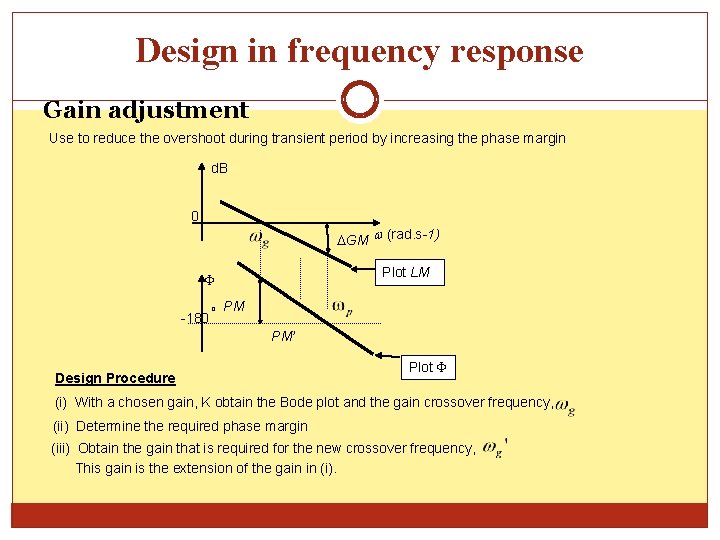
Design in frequency response Gain adjustment Use to reduce the overshoot during transient period by increasing the phase margin d. B 0 GM (rad. s-1) Plot LM -180 o PM PM’ Design Procedure Plot (i) With a chosen gain, K obtain the Bode plot and the gain crossover frequency, (ii) Determine the required phase margin (iii) Obtain the gain that is required for the new crossover frequency, This gain is the extension of the gain in (i).

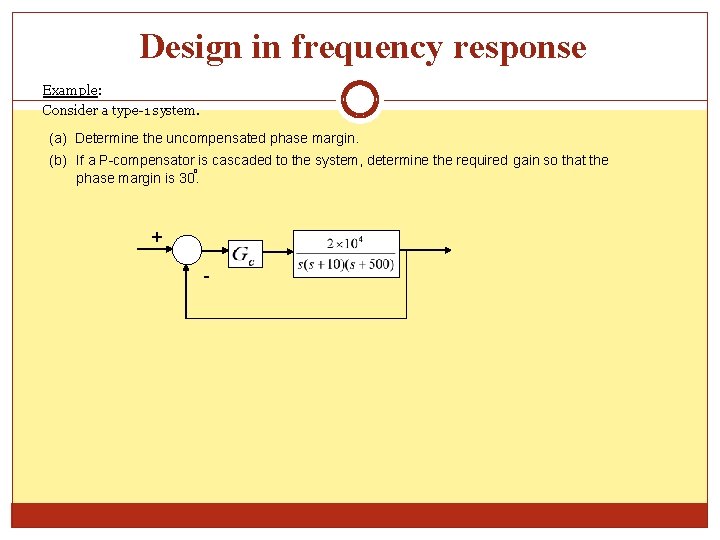
Design in frequency response Example: Consider a type-1 system. (a) Determine the uncompensated phase margin. (b) If a P-compensator is cascaded to the system, determine the required gain so that the o phase margin is 30. + -

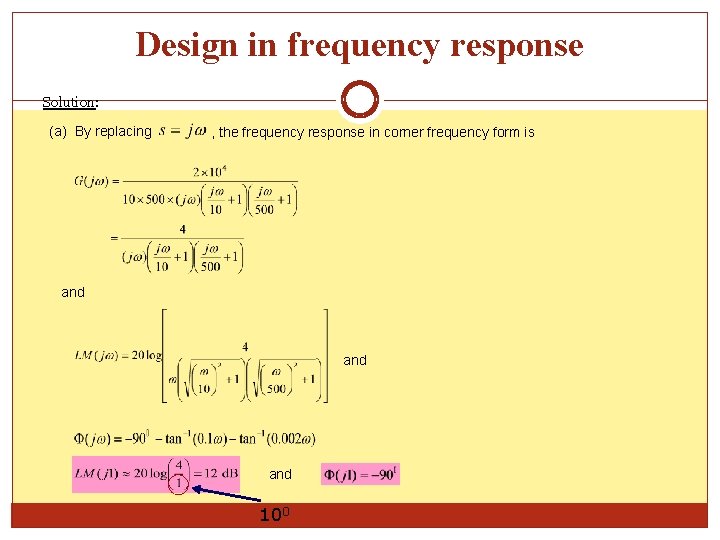
Design in frequency response Solution: (a) By replacing , the frequency response in corner frequency form is and and 100

Design in frequency response (rad. s-1) Pole at origin 1 10 500 -20 -20 -20 0 0 -20 -40 -60 (d. B/dekad) Real pole (d. B/dec) Total slope (d. B/dec) and

Design in frequency response (rad. s-1) 1 50 100 5000 Real pole -45 0 0 0 -45 -90 -45 0 (deg/dec) Real pole (deg/dec) Total slope (deg/dec) and

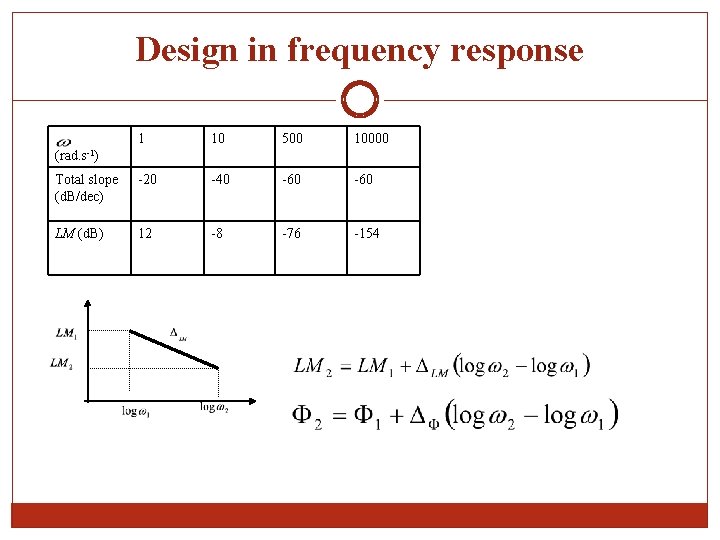
Design in frequency response 1 10 500 10000 Total slope (d. B/dec) -20 -40 -60 LM (d. B) 12 -8 -76 -154 (rad. s-1)

Design in frequency response (rad. s-1) 1 50 100 5000 10000 Total slope (deg/dec) -45 -90 -45 0 0 -90 -166 -193 -269 (deg) >> w 1=[1 10 500 10000]; LM=[12 -8 -76 -154]; >> w 2=[1 50 100 5000 10000]; ph=[-90 -166 -193 -269]; >> subplot(2, 1, 1); semilogx(w 1, LM); subplot(2, 1, 2); semilogx(w 2, ph); From the Bode plot, and for uncompensated system

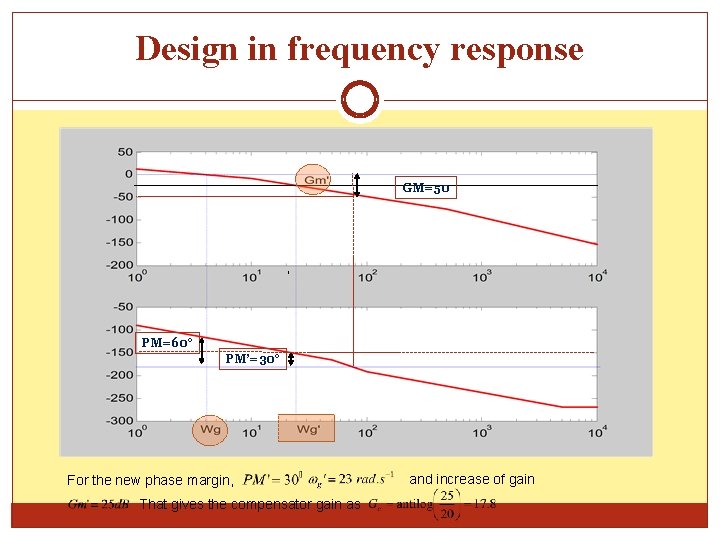
Design in frequency response That gives the compensator gain as GM=50 , PM=60° PM’=30° For the new phase margin, That gives the compensator gain as and increase of gain

Design in frequency response Lag compensator The compensator can also be presented as where . The pole is chosen to be closed with the origin, example As the zero is far away from the pole, no obvious transient response will be affected Increased in the open-loop gain will improve the steady state error

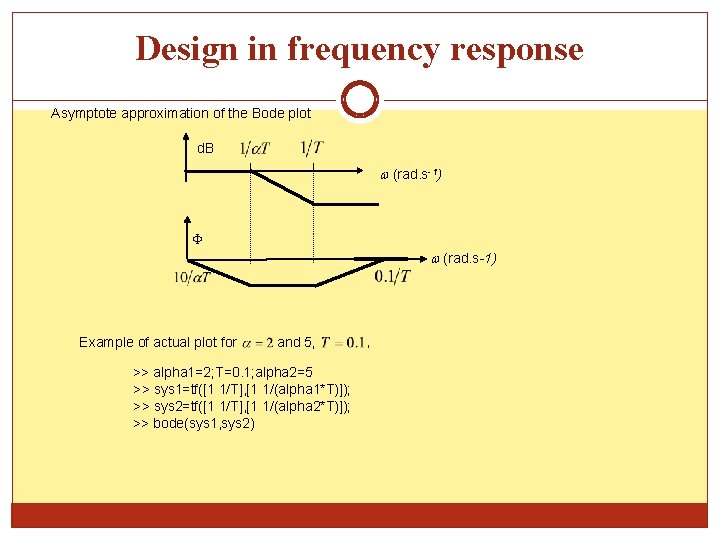
Design in frequency response Asymptote approximation of the Bode plot d. B (rad. s-1) Example of actual plot for and 5, >> alpha 1=2; T=0. 1; alpha 2=5 >> sys 1=tf([1 1/T], [1 1/(alpha 1*T)]); >> sys 2=tf([1 1/T], [1 1/(alpha 2*T)]); >> bode(sys 1, sys 2) ,

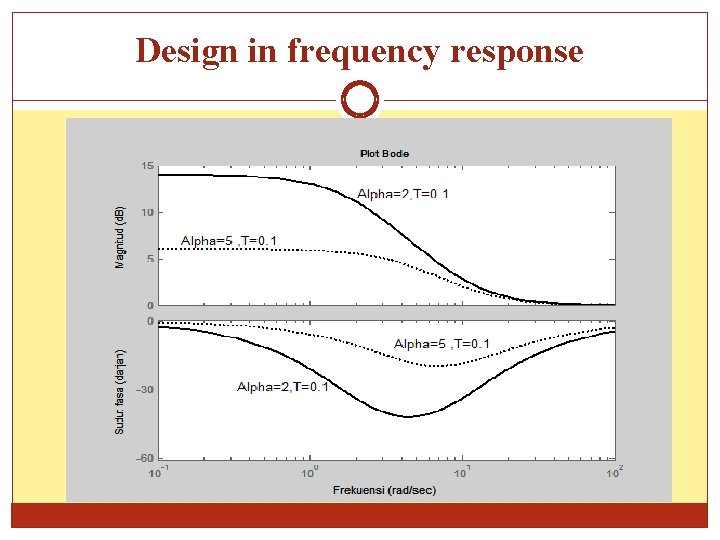
Design in frequency response

Design in frequency response Observation from the plot: At low frequency, the compensator will not have influenced on the open-loop gain so we can increased the gain for steady state improvement Design Procedure Design procedures are as follow: (i) Determine the gain K for the required steady state error and draw the Bode plot (ii) Obtained the required phase margin and add, compensator phase angle, =5 - 12 (iii) Compensator’s zero will be a decade below of the new gain crossover frequency of (ii). (iv) Compensator’s pole is obtained by drawing a slope of -20 d. B/dec from the compensator’s zero until the line touched the 0 d. B.

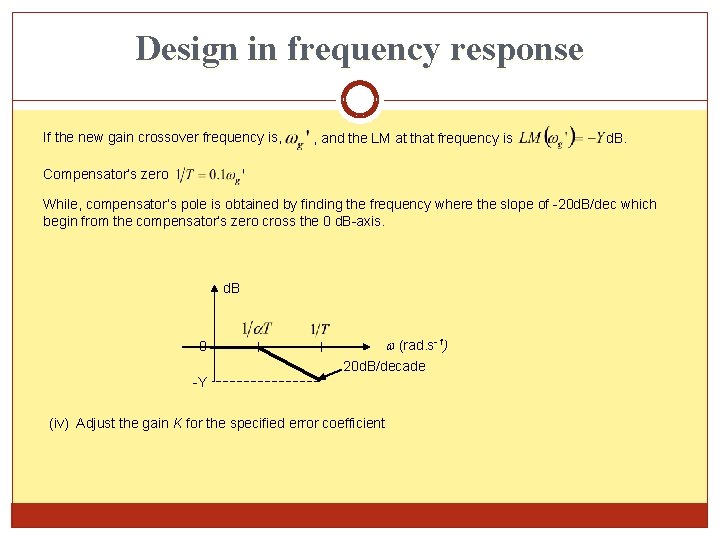
Design in frequency response If the new gain crossover frequency is, , and the LM at that frequency is d. B. Compensator’s zero While, compensator’s pole is obtained by finding the frequency where the slope of -20 d. B/dec which begin from the compensator’s zero cross the 0 d. B-axis. d. B (rad. s-1) 0 -Y 20 d. B/decade (iv) Adjust the gain K for the specified error coefficient

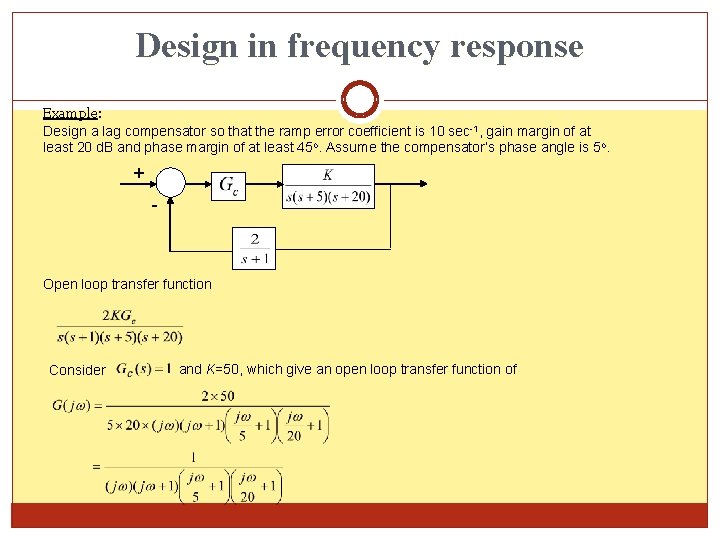
Design in frequency response Example: Design a lag compensator so that the ramp error coefficient is 10 sec-1, gain margin of at least 20 d. B and phase margin of at least 45 o. Assume the compensator’s phase angle is 5 o. + - Open loop transfer function Consider and K=50, which give an open loop transfer function of

Design in frequency response and >> w 1=[0. 1 1 5 20 1000]; LM=[20 0 -28 -64 -120 -200]; >> w 1 a=[0. 1 1000]; LMa=[0 0]; >> subplot(2, 1, 1); semilogx(w 1, LM, w 1 a, LMa, '-'); >> w 2=[0. 1 0. 5 2 10 50 200 1000]; ph=[-90 -121 -176 -270 -333 -360]; >> w 2 a=[0. 1 1000]; pha=[-180]; >> subplot(2, 1, 2); semilogx(w 2, ph, w 2 a, pha, '-'); From the Bode plot

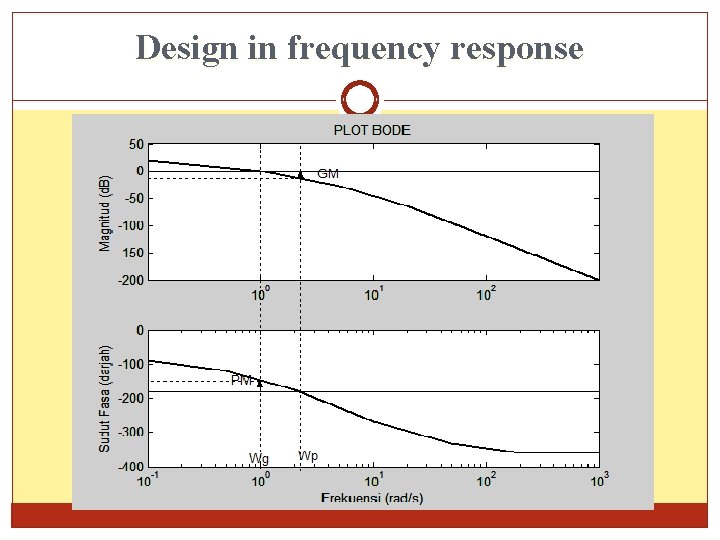
Design in frequency response

Design in frequency response Given Open loop transfer function without compensator with initial value of Thus shift 20 d. B upward from original plot. New phase margin with =5 o, PM’=45 o+5 o=50 o. thus Hence the compensator must provide – 20. ’=0. 65 rad. s-1.

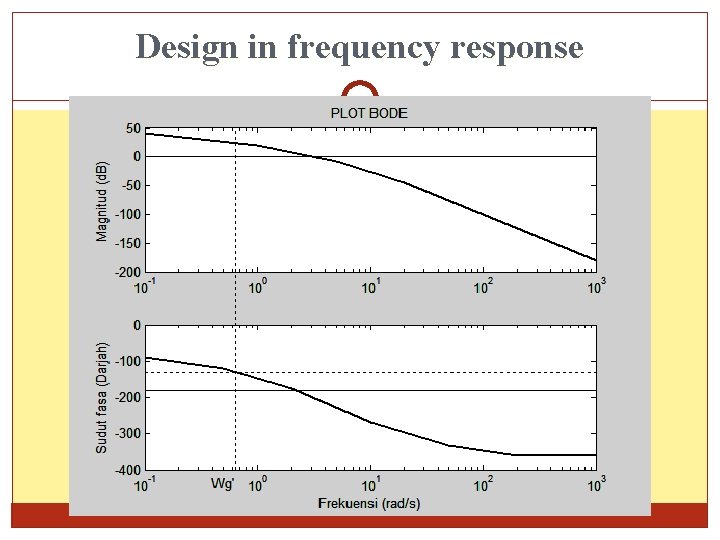
Design in frequency response

Design in frequency response >> w 1=[0. 1 1 5 20 1000]; LM=[40 20 -8 -44 -100 - 180]; >> w 1 a=[0. 1 1000]; LMa=[0 0]; >> subplot(2, 1, 1); semilogx(w 1, LM, w 1 a, LMa, '-'); title('PLOT BODE'); ylabel('Magnitud (d. B)') >> w 2=[0. 1 0. 5 2 10 50 200 1000]; ph=[-90 -121 -176 -270 -333 360 -360]; >> w 2 a=[0. 1 1000]; pha=[-180]; >> w 2 b=[0. 1 1000]; phb=[-130]; At >>subplot(2, 1, 2); semilogx(w 2, ph, w 2 a, pha, w 2 b, phb, '’, '); xlabel('Frekuensi (rad/s)'); ylabel('Sudut fasa (Darjah)') At ’,

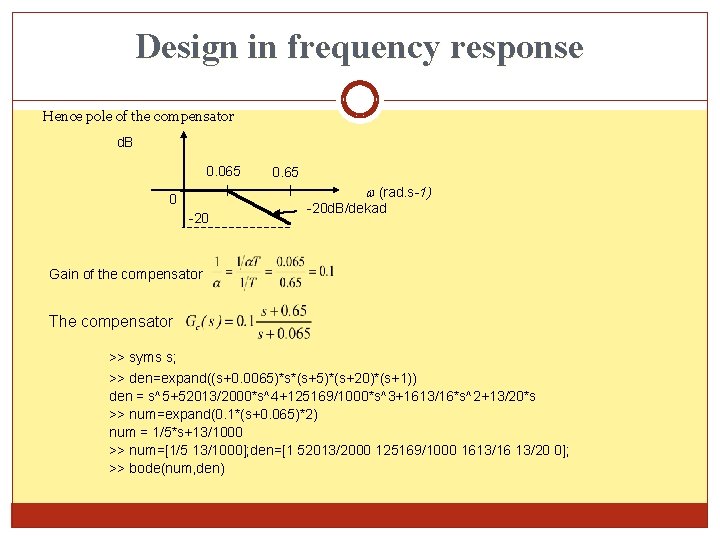
Design in frequency response Hence pole of the compensator d. B 0. 065 0 -20 0. 65 (rad. s-1) -20 d. B/dekad Gain of the compensator The compensator >> syms s; >> den=expand((s+0. 0065)*s*(s+5)*(s+20)*(s+1)) den = s^5+52013/2000*s^4+125169/1000*s^3+1613/16*s^2+13/20*s >> num=expand(0. 1*(s+0. 065)*2) num = 1/5*s+13/1000 >> num=[1/5 13/1000]; den=[1 52013/2000 125169/1000 1613/16 13/20 0]; >> bode(num, den)

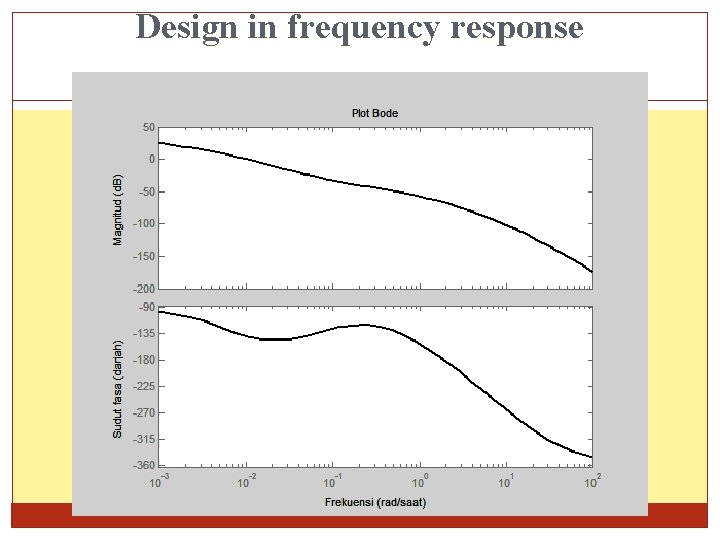
Design in frequency response

Design in frequency response >> syms s; >> den=expand((s+0. 065) *s*(s+5)*(s+20)*(s+1)) den = s^5+5213/200*s^4+12669/100*s^3+865/8*s^2+13/2*s >> num=expand(0. 1*(s+0. 65)*2) num = 1/5*s+13/100 >> num=[1/5 13/100]; den=[1 5213/200 12669/100 865/8 13/2 0]; >> bode(num, den) >> num=[1/5 13/100]; den=[1 5213/200 12669/100 865/8 13/2 0]; bode(num, den) sys=tf(num, den); [GM, PM, Wg, Wp] = margin(sys) GM_d. B = 20*log 10(Gm) GM = 693. 1782 PM = 73. 8732 Wg = 1. 0751 Wp = 0. 0192 GM_d. B = 56. 8169