Controller and Observer Design Design of Control System

Controller and Observer Design (Design of Control System in State Space) (Design of Control System in State Space by Pole placement)

References • Dr. Radhakant Padhi, Asstt. Prof, IISC, Bangalore, through NPTEL • Modern Control Engineering by Katsuhiko Ogata, PHI Pvt. Ltd New Delhi

Pole Placement Controller Design

Pole Placement Technique • Poles of a control system (stable/unstable) can be place at desired location by pole placement technique. This is done to • • • Improve the performance of the system Make the system stable Increase the damping Increase the response time Etc

Pole Placement Technique • Assumptions are 1. The system is completely state controllable 2. The sate variable are measureable and available for feedback 3. Control input (u) is unconstrained and single Note: For multi input system, the state feedback gain matrix is not unique

Pole Placement Technique •

Philosophy of Pole placement control design •
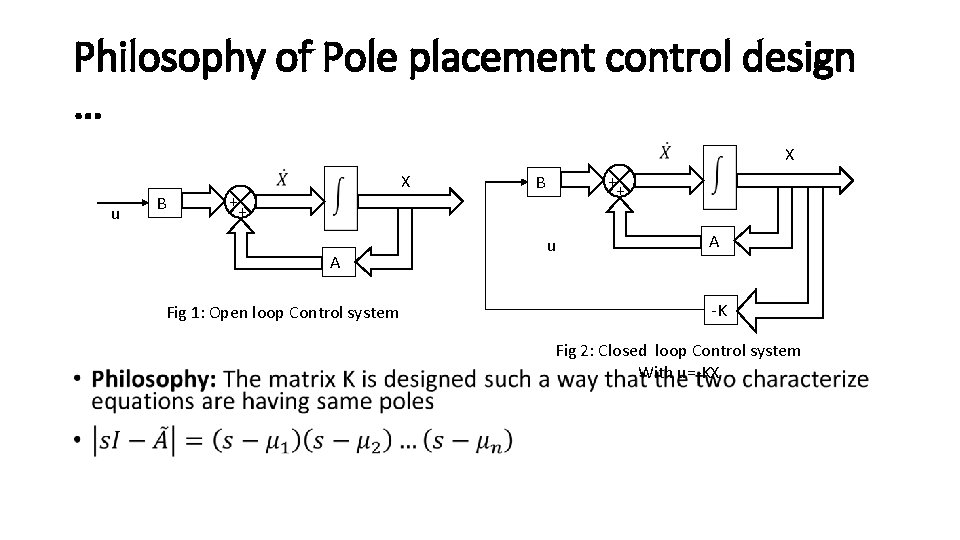
Philosophy of Pole placement control design … • u B + + A Fig 1: Open loop Control system X ++ B u X A -K Fig 2: Closed loop Control system With u=-KX

Placement control design (Controller Design) • There are three method: • Method 1: Direct substitution method (when order of system n≤ 3) • Method 2: Bass-Gura Approach • Method 3: Ackermann’s formula

Controller Design by method 1: •

Controller Design by method 2: •
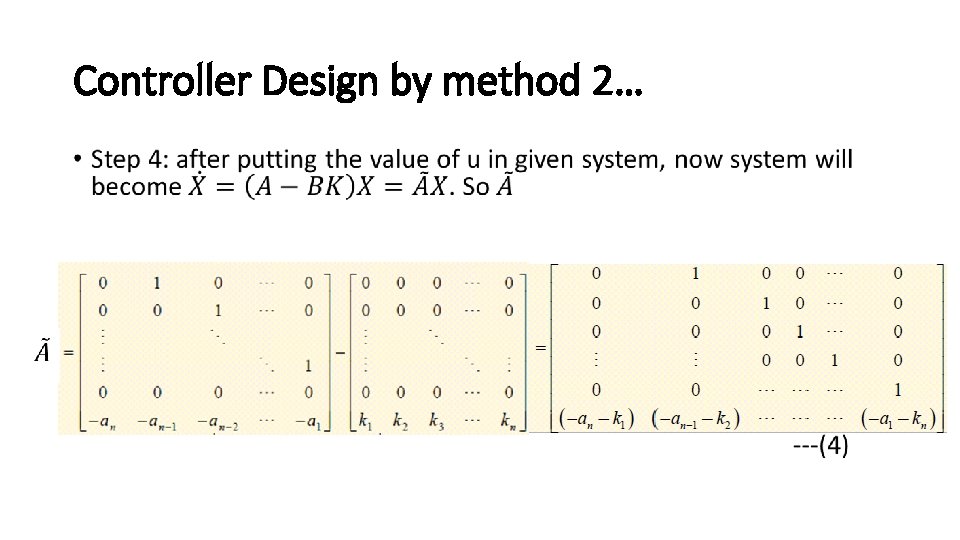
Controller Design by method 2… •

Controller Design by method 2… • Step 5: ---(5)

Controller Design by method 2… • Step 6: Comparing equations (4) & (5) we have

What if the system is not given in first companion form? •

What if the system is not given in first companion form? . . .

Controller Design using Method 2: Bass-Gura Approach •

Controller Design using Method 3: Ackermann’s Formula •

Controller Design using Method 3: Ackermann’s Formula … •

Controller Design using Method 3: Ackermann’s Formula … • 0

Controller Design using Method 3: Ackermann’s Formula … • => • Since system is completely controllable inverse of the controllability matrix exists we obtain => ---(7)
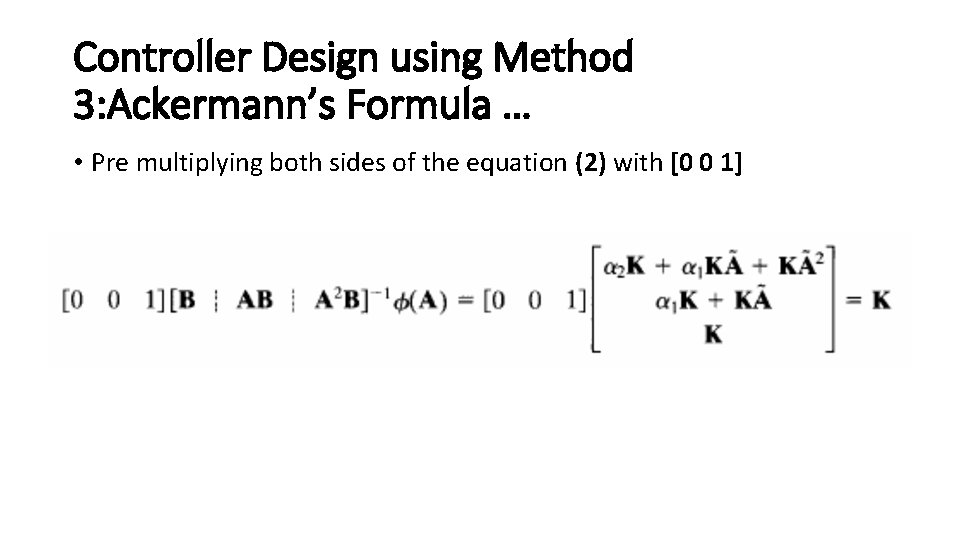
Controller Design using Method 3: Ackermann’s Formula … • Pre multiplying both sides of the equation (2) with [0 0 1]

Controller Design using Method 3: Ackermann’s Formula … •

Example •

Example. . •

Example. . •

Example… •

Example •

Example… •

Example… •
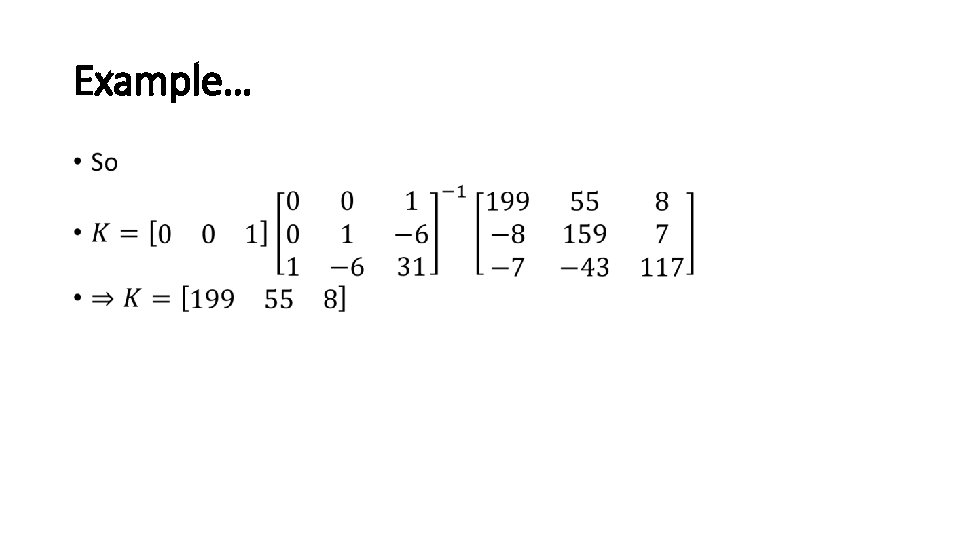
Example… •

Choice of closed loop poles: • Don’t choose the closed loop poles far away from the open loop poles, otherwise it will damage high control effort. • Don’t choose the closed loop poles very negative, otherwise the system will be fast reacting (i. e it will have a small time constant) • In frequency domain it will lead to large bandwidth and hence noise get amplified.

Controller for multi input system • The state feedback gain matrix (K) becomes a matrix of mxn (Not vector of 1 xn unlike single input system) • m = no of inputs and n = no of states • The state feedback gain matrix (K) is not unique
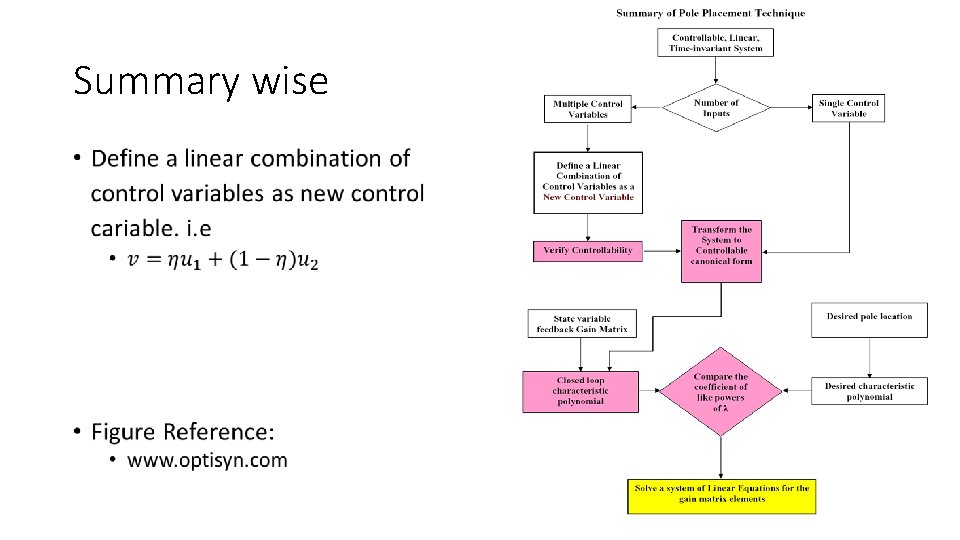
Summary wise •

Next: Observer Design Thanks
- Slides: 35