Controlled Release Estimation of the Diffusion Coefficient 1

Controlled Release Estimation of the Diffusion Coefficient 1

Stokes-Einstein Relation n For free diffusion n k = Boltzman Constant q n q Assumes a spherical molecule n i. e. , not valid for a longchain protein n n 1. 38 x 10 -23 J/K η = solvent viscosity (kg/ms) T is temperature (K) r is solute molecule radius q related to molecular weight 2

Stokes-Einstein Relation n Radius, r, is related to MW n n n Solve for r n Substitute into S-E eqn q n N is Avagadro’s Number V is the molal volume of the solute. r is the hydrodynamic radius, which considers solvent bound to solute Note D is not a strong fn of MW 3

Diffusion Coefficient n Many drugs have a low molecular wt q q n 100 < MW < 500 g/mol Not true for proteins and larger molecules Examples Drug MW (g/mol) D(cm 2/s) Aqueous Note Caffeine 194. 2 4. 9 x 10 -6 Medium size Insulin 41, 000 8. 3 x 10 -7 Huge size 4

Sutherland-Einstein Correlation n Sutherland-Einstein Equation q q q More reliable prediction for smaller solutes. Modification of Stokes-Einstein, which considers sliding friction between solute and solvent. For large molecules, β approaches infinity to reflect “no slip” conditions, and the equation reduces to the Stokes-Einstein relation 5

Wilke-Chang Correlation n Semi-empirical modification of the Stokes-Einstein relation. 10 -15% error. Widely used for small molecules in low MW solvents, at low concentrations. Involves q q q MW of solvent Absolute temperature Solvent viscosity Solute molal volume at normal BP Association factor of solvent (2. 6 for water, 1. 9 for methanol, 1. 5 for Et. OH) 6

Diffusion Coefficients in Polymers n For large pores q q n For small pores q q n Diffusion through liquid filled pores Steric hindrance, friction For non-porous polymer networks q q n diffusion through liquid filled pores Porosity, tortuosity, partition coefficient Complicated; various mechanisms proposed Depends on crystallinity, swelling, crosslinking, rubbery vs. glassy state Predictions based on semi-empirical or empirical approaches 7

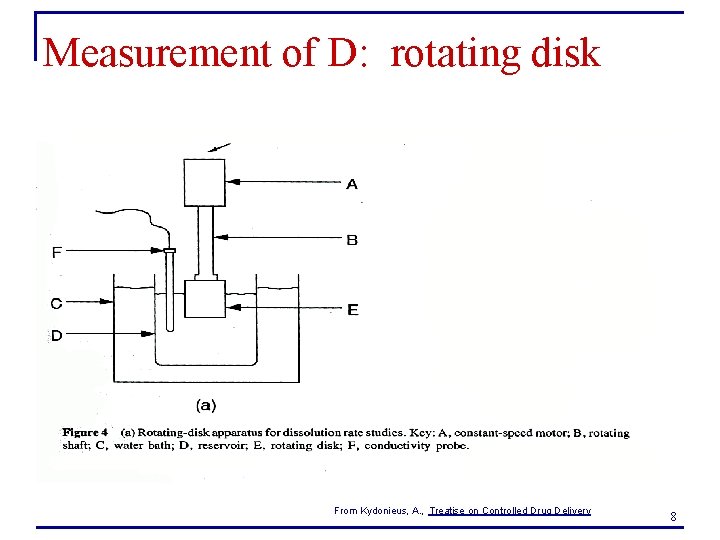
Measurement of D: rotating disk From Kydonieus, A. , Treatise on Controlled Drug Delivery 8

Measurement of diffusion coefficient n Rotating disk for measurement of D in liquids q q q n Considers the rate of dissolution of a drug from a disk spinning in a liquid Q is rate of dissolution A is surface area of drug on disk vo is the kinematic viscosity of the solvent, Cs is the drug solubility in the solvent ω is the rotational speed of the disk Perform experiments at different ω. What plot will give a slope of D? q Q vs. ω 0. 5 9

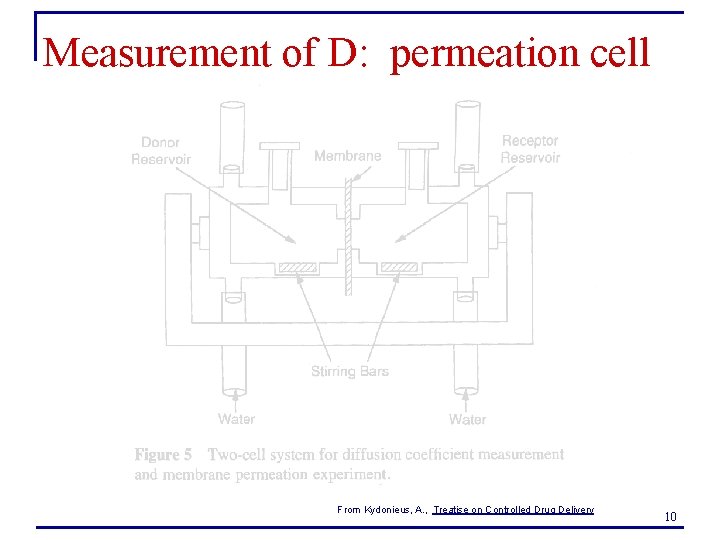
Measurement of D: permeation cell From Kydonieus, A. , Treatise on Controlled Drug Delivery 10

Measurement of diffusion coefficient n Two Cell Permeation System q q For D in liquids or polymers Two stirred cells divided by a membrane. Initially one contains the drug in suspension. n n n LHS is the steady-state permeation rate K is the partition coefficient (membrane/solution) L is the membrane thickness 11

Measurement of diffusion coefficient n n More methods for polymers Direct release method – curve fitting from a release experiment. q n Usually preferable to determine through independent experiments. Sorption and desorption from stirred finite volume q q Simple experiment Mathematics of diffusion through a solid will be investigated later 12

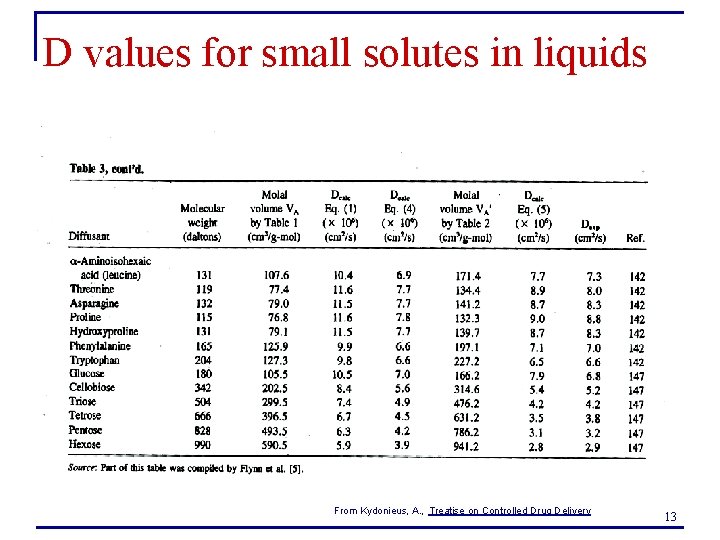
D values for small solutes in liquids From Kydonieus, A. , Treatise on Controlled Drug Delivery 13

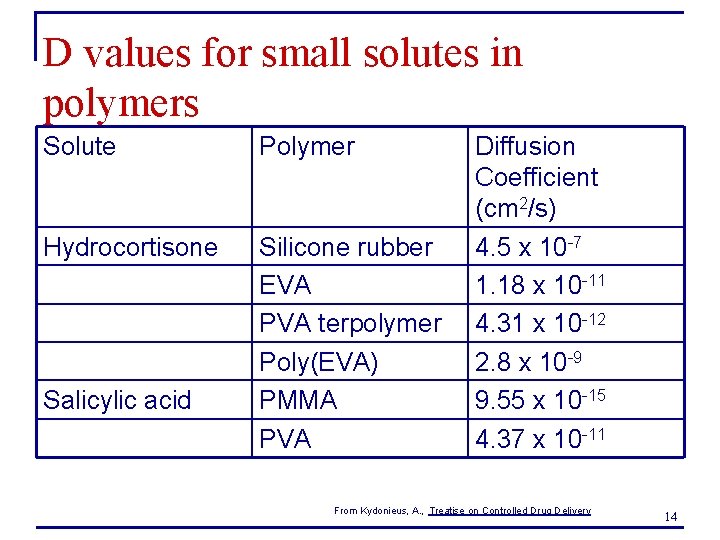
D values for small solutes in polymers Solute Polymer Hydrocortisone Silicone rubber EVA PVA terpolymer Poly(EVA) PMMA PVA Salicylic acid Diffusion Coefficient (cm 2/s) 4. 5 x 10 -7 1. 18 x 10 -11 4. 31 x 10 -12 2. 8 x 10 -9 9. 55 x 10 -15 4. 37 x 10 -11 From Kydonieus, A. , Treatise on Controlled Drug Delivery 14