Controllability of feedback systems Sigurd Skogestad Department of

Controllability of feedback systems Sigurd Skogestad Department of Chemical Engineering Norwegian University of Science and Tecnology (NTNU) Trondheim, Norway Workshop: Modelling of astrocyte function June 8, 2006, University of Oslo 1

NTNU, Trondheim 2

Motivation • I have co-authored a book: ”Multivariable feedback control – analysis and design” (Wiley, 1996, 2005) – What parts could be useful for system biology? • Control as a field is closely related to systems theory • Here: Focus on the use of negative feedback • Some other areas where control may contribute (Not covered): – – 3 Identification of dynamic models from data (not in my book anyway) Model reduction Nonlinear control (also not in my book) Discrete event and hybrid systems (also not in my book)

Outline 1. Overview of control theory and concepts 2. Feedback • • Positive and negative feedforward Simple example: Feedforward vs. feedback Problem feedback: (Effective) Time delay Cascade control 3. Control hierarchies • • • Time scale separation Controlled variables Self-optimizing control 4. Summary and concluding remarks 4

Overview of Control theory • Classical feedback control (1930 -1960) (Bode): – – – • Optimal control (1960 -1980) (Kalman): – – – • Combine classical and optimal control Optimal design of controllers with guaranteed robustness (H∞) Nonlinear control (1950 - ) – 5 Optimal design of Multivariable (MIMO) controllers Model-based ”feedforward” thinking; no robustness guarantees (LQG) State-space formulation (A, B, C, D); Advanced mathematical tools (LQG) Robust control (1980 -1995) (Zames, J. C. Doyle) – – • Single-loop (SISO) feedback control Transfer functions, Frequency analysis (Bode-plot) Fundamental feedback limitations (waterbed). Focus on robustness ”Feedforward thinking”, mostly mechanical systems • Adaptive control (1970 -1985) (Åstrøm) • Discrete event and hybrid systems – – Automata theory Computer science

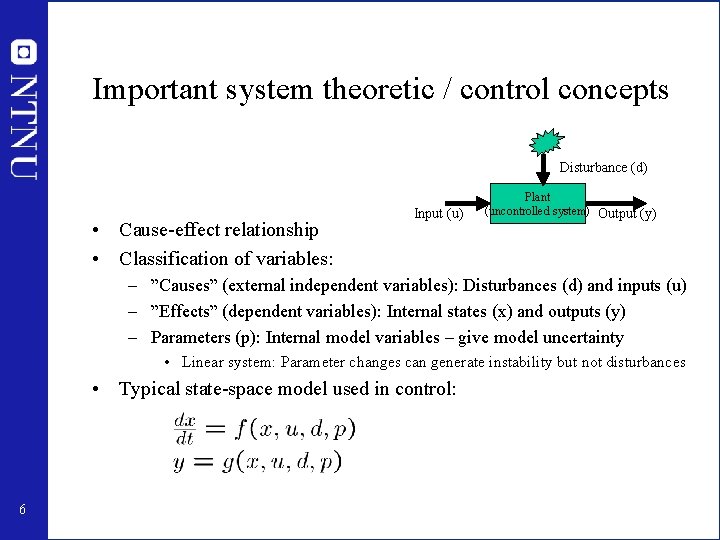
Important system theoretic / control concepts Disturbance (d) • Cause-effect relationship • Classification of variables: Input (u) Plant (uncontrolled system) Output (y) – ”Causes” (external independent variables): Disturbances (d) and inputs (u) – ”Effects” (dependent variables): Internal states (x) and outputs (y) – Parameters (p): Internal model variables – give model uncertainty • Linear system: Parameter changes can generate instability but not disturbances • Typical state-space model used in control: 6

Linearized model descriptions (useful for analysis and controller design) • State space realization • Transfer function realization (input-output model) • Frequency analysis 7

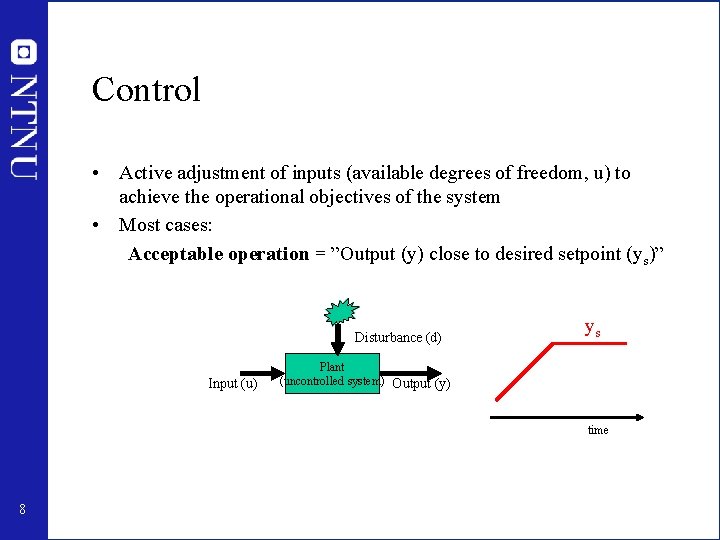
Control • Active adjustment of inputs (available degrees of freedom, u) to achieve the operational objectives of the system • Most cases: Acceptable operation = ”Output (y) close to desired setpoint (ys)” Disturbance (d) Input (u) ys Plant (uncontrolled system) Output (y) time 8

Control theory Design 9

Control theory concepts • Steady-state = Equilibrium point = DC • Poles/modes/eigenvalues: Characteristic of dynamic response of system associated with system states – Model (= our realization of the real system): • (state) Controllability • (state) Observability • Zeros: Characteristic of dynamic response of system inverse • Stability – System maintains equilibrium point (Lyapunov stability) – Linear system (local behaviour): • Stable = eigenvalue/pole in left half plane (LHP) • Unstable = eigenvalue/pole(s) in right half plane (RHP) 10

Robustness • • Insensitivity of system behavior to uncertainty (parameter variations) Most real biological systems are robust Robustness generally requires negative feedback Measures and tools for robustness analysis – – 11 Uncertainty representation Stability margins Positivity, small gain theorem Structured singular value (Doyle)

(Input-Output) Controllability • Input-output: Is the system inherently controllable? • First requirement: Stabilization • ‘‘Natural” (open-loop = without control) unstable system: – Can not be stabilized with feedforward control – Can only be stabilized by feedback – Must require that any unstable modes are detectable and stabilizable – Detectable: Unstable modes observable in the outputs – Stabilizable: Unstable modes controllable by the inputs • Next requirement: performance 12

Controllability limitations (performance) Serious limitations: 1. (Effective) Time delay in direct path from input to output – Want input close to output 2. Unstable inverse (RHP-zeros) – Limits input-output controllability because system inverse is unstable Other limitations: 3. 4. 5. 6. 13 Large disturbances Small process gain (inputs weakly affect outputs) Unstable system (even if unstable modes are detectable and stabilizable) Nonlinearity

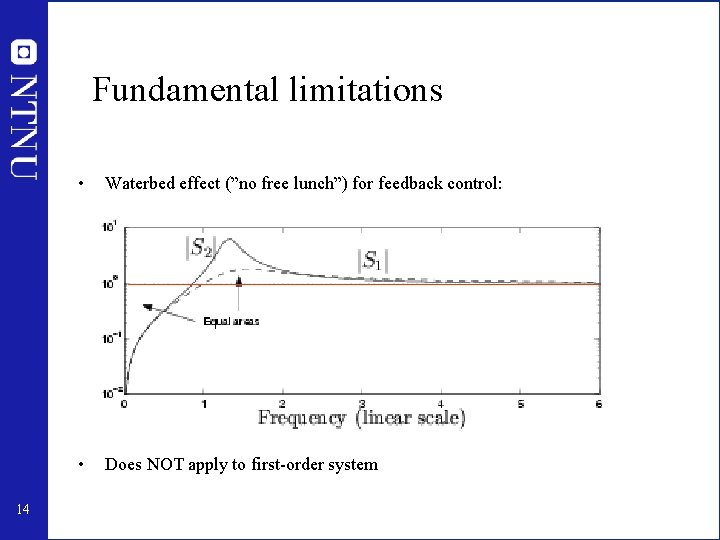
Fundamental limitations 14 • Waterbed effect (”no free lunch”) for feedback control: • Does NOT apply to first-order system

FEEDBACK 15

Positive and negative feedback in biological systems (from Wipikedia) • Positive feedback amplifies possibilities of divergences (evolution, change of goals); it is the condition to change, evolution, growth; it gives the system the ability to access new points of equilibrium. – For example, in an organism, most positive feedbacks provide for fast autoexcitation of elements of endocrine and nervous systems (in particular, in stress responses conditions) and play a key role in regulation of morphogenesis, growth, and development of organs, all processes which are in essence a rapid escape from the initial state. Homeostasis is especially visible in the nervous and endocrine systems when considered at organism level. • Negative feedback helps to maintain stability in a system in spite of external changes. It is related to homeostasis. – Negative feedback combined with time delay can give instability: A well known example in ecology is the oscillation of the population of snowshoe hares due to predation from lynxes. – Le Chateliers principle for stable equilibrium (OK for main effect): 16 • Systems responds by counteracting effect of disturbance

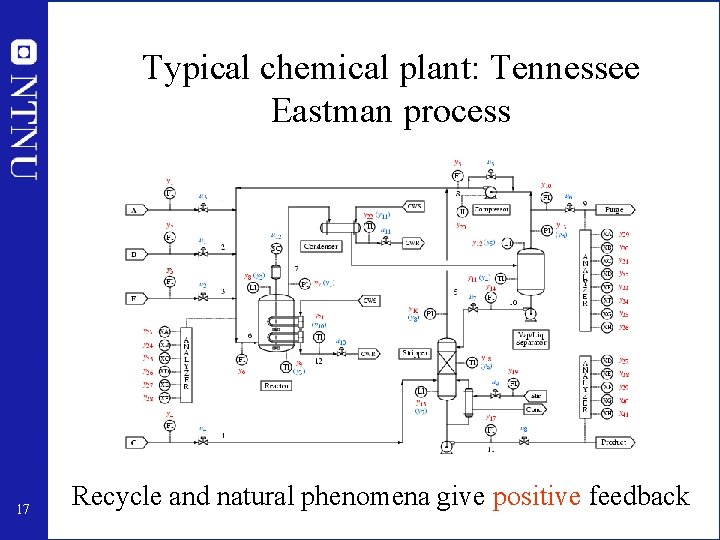
Typical chemical plant: Tennessee Eastman process 17 Recycle and natural phenomena give positive feedback

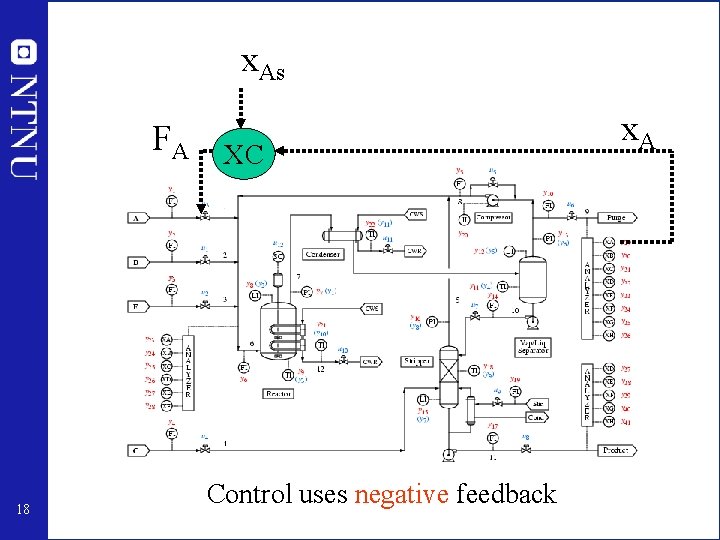
x. As FA 18 XC Control uses negative feedback x. A

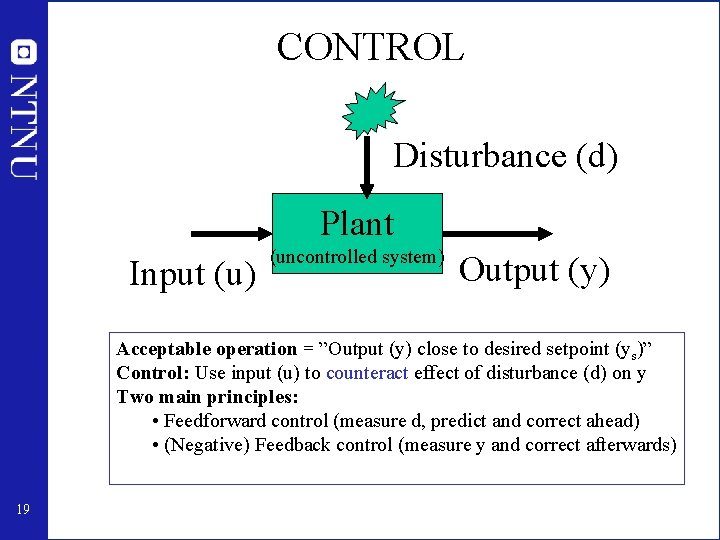
CONTROL Disturbance (d) Plant Input (u) (uncontrolled system) Output (y) Acceptable operation = ”Output (y) close to desired setpoint (ys)” Control: Use input (u) to counteract effect of disturbance (d) on y Two main principles: • Feedforward control (measure d, predict and correct ahead) • (Negative) Feedback control (measure y and correct afterwards) 19

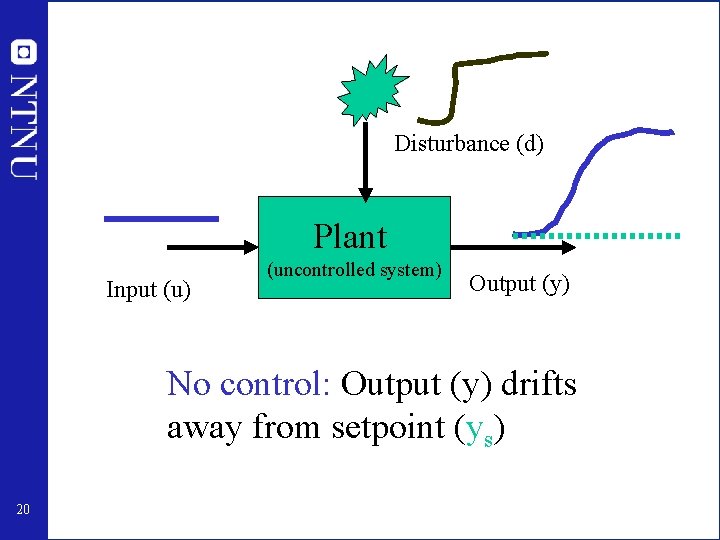
Disturbance (d) Plant Input (u) (uncontrolled system) Output (y) No control: Output (y) drifts away from setpoint (ys) 20

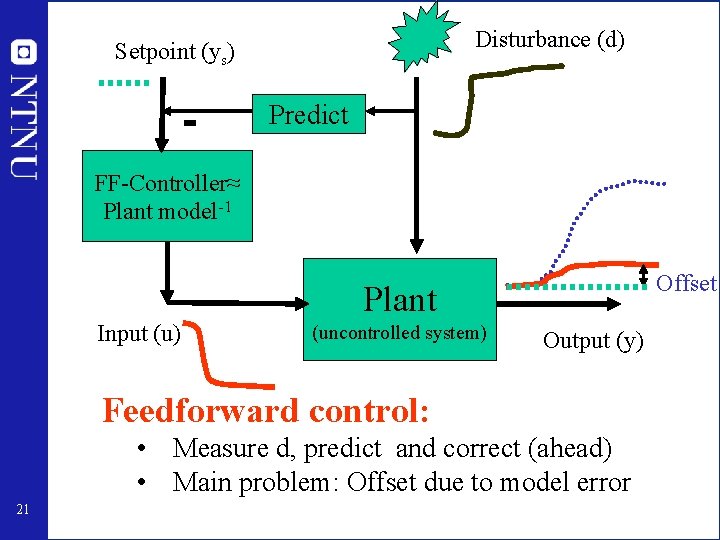
Disturbance (d) Setpoint (ys) Predict FF-Controller≈ Plant model-1 Offset Plant Input (u) (uncontrolled system) Output (y) Feedforward control: • Measure d, predict and correct (ahead) • Main problem: Offset due to model error 21

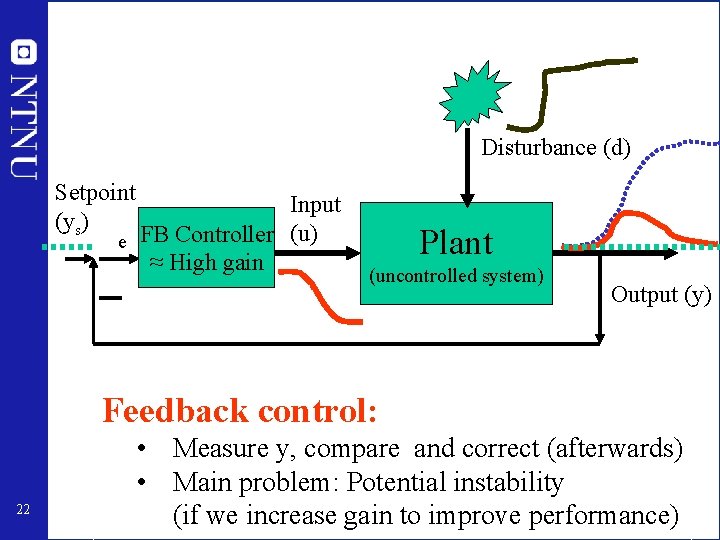
Disturbance (d) Setpoint (ys) Input e FB Controller (u) ≈ High gain Plant (uncontrolled system) Output (y) Feedback control: 22 • Measure y, compare and correct (afterwards) • Main problem: Potential instability (if we increase gain to improve performance)

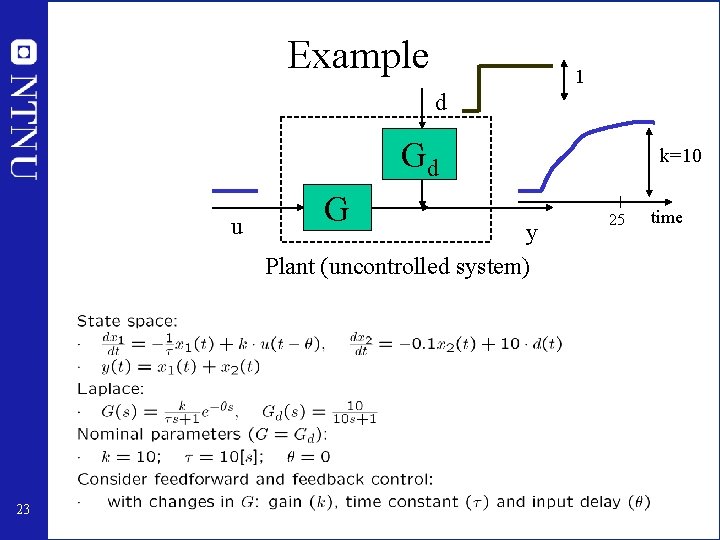
Example 1 d Gd u 23 G y Plant (uncontrolled system) k=10 25 time

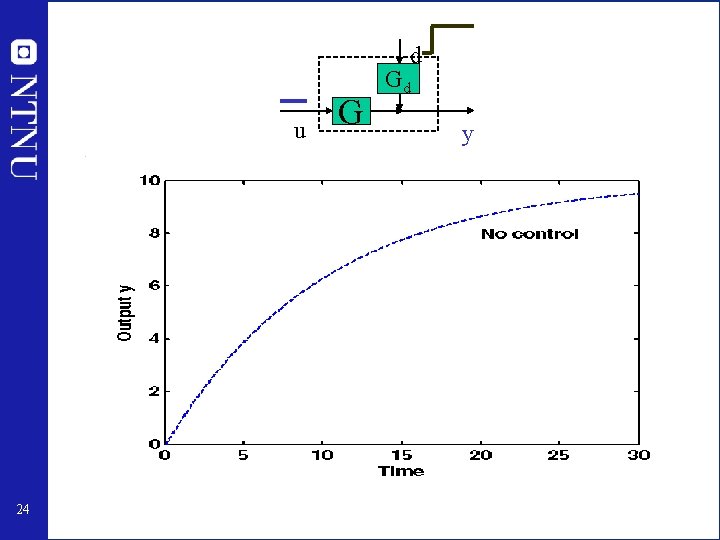
d u 24 G Gd y

Model-based control = Feedforward (FF) control d Gd u G y ”Perfect” feedforward control: u = - G-1 Gd d Our case: G=Gd → Use u = -d 25

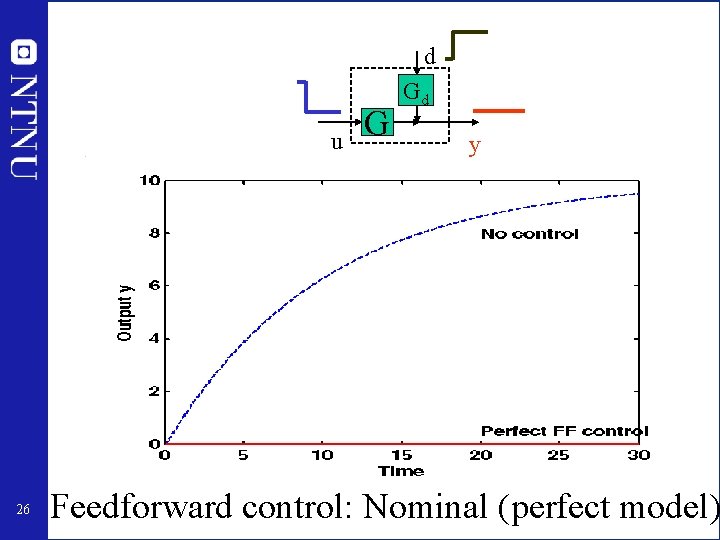
d u 26 G Gd y Feedforward control: Nominal (perfect model)

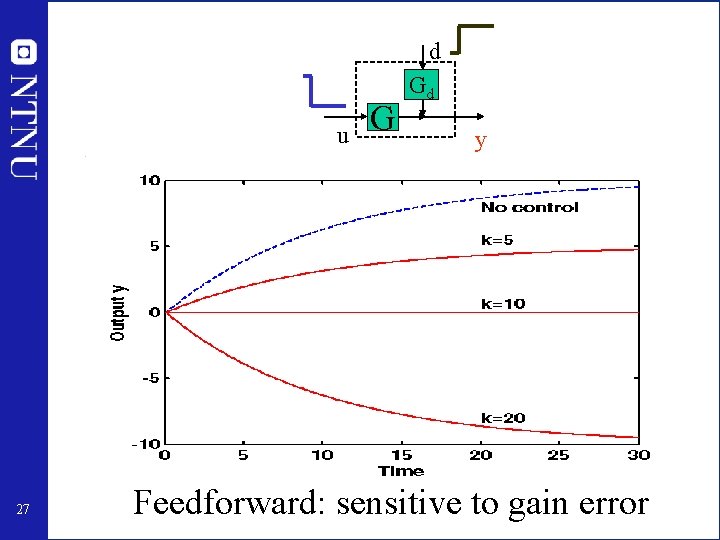
d u 27 G Gd y Feedforward: sensitive to gain error

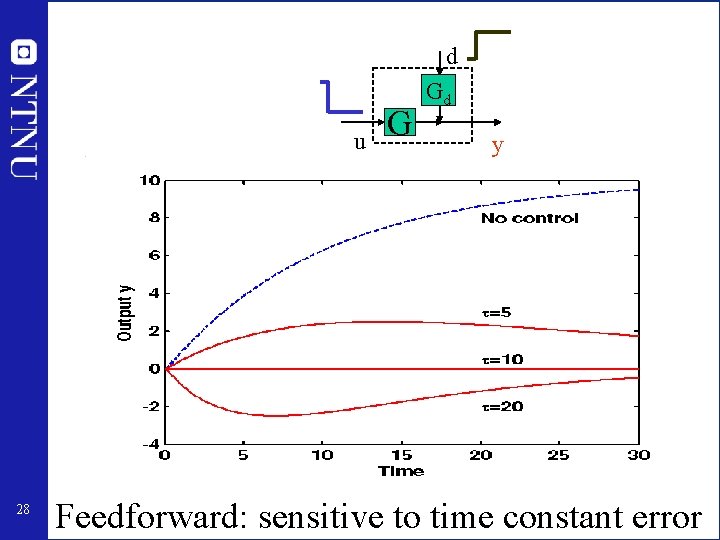
d u 28 G Gd y Feedforward: sensitive to time constant error

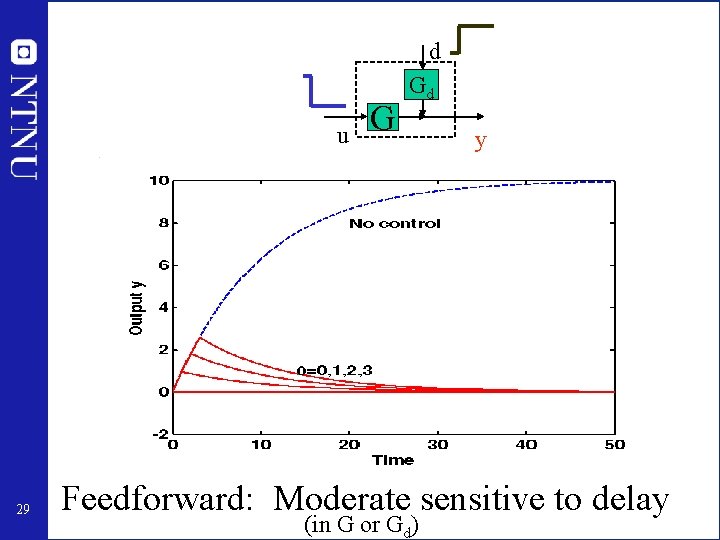
d u 29 G Gd y Feedforward: Moderate sensitive to delay (in G or Gd)

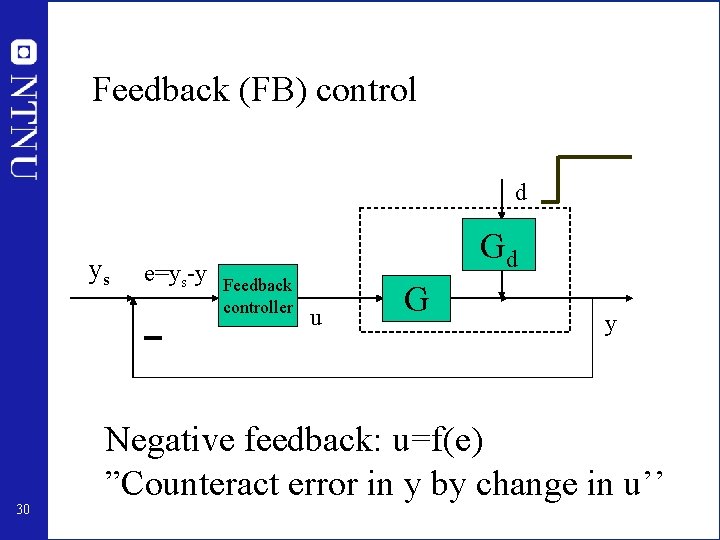
Feedback (FB) control d ys 30 e=ys-y Gd Feedback controller u G y Negative feedback: u=f(e) ”Counteract error in y by change in u’’

Feedback (FB) control e=ys-y Feedback controller u Simplest: On/off-controller • u varies between umin (off) and umax (on) • Problem: Continous cycling 31

Feedback (FB) control e=ys-y Feedback controller u Most common in industrial systems: PI-controller 32

Back to the example d u 33 G Gd y

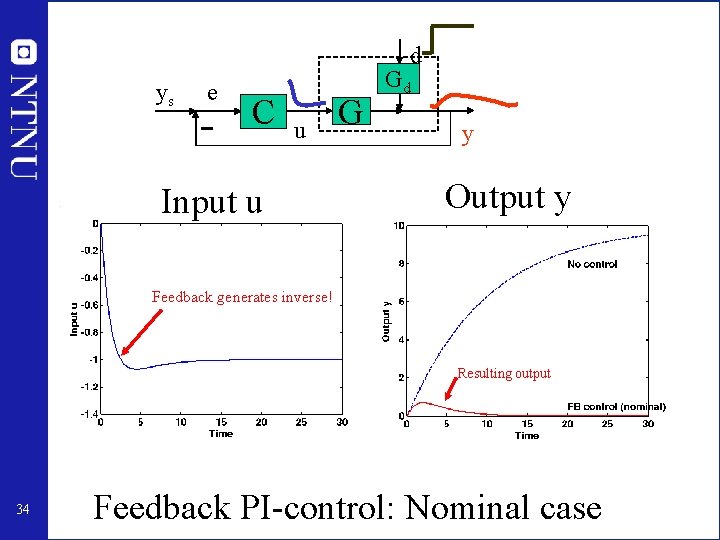
d ys e C u Input u G Gd y Output y Feedback generates inverse! Resulting output 34 Feedback PI-control: Nominal case

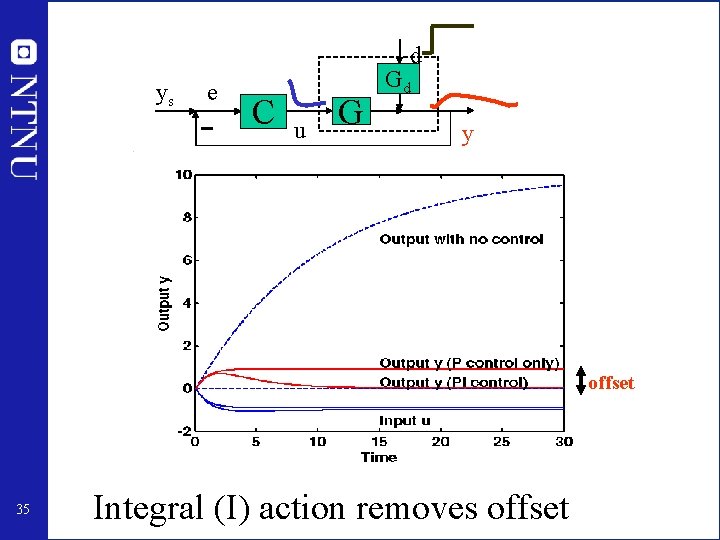
d ys e C u G Gd y offset 35 Integral (I) action removes offset

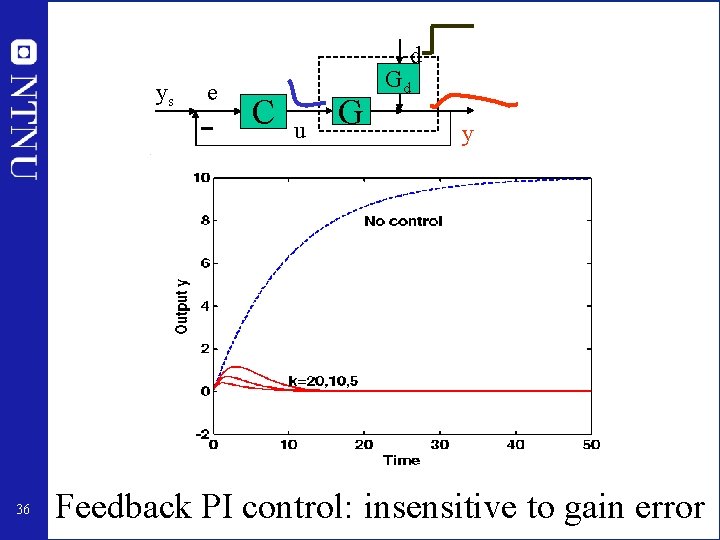
d ys 36 e C u G Gd y Feedback PI control: insensitive to gain error

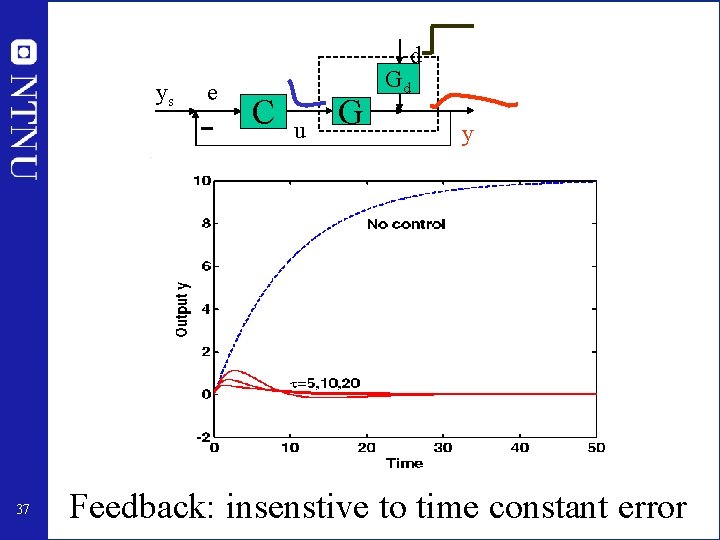
d ys 37 e C u G Gd y Feedback: insenstive to time constant error

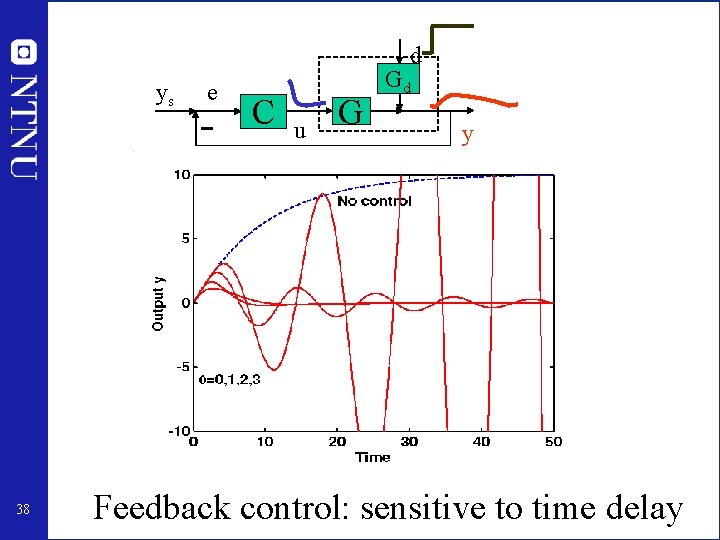
d ys 38 e C u G Gd y Feedback control: sensitive to time delay

Summary example • Feedforward control is NOT ROBUST (it is sensitive to plant changes, e. g. in gain and time constant) • Feedforward control: gradual performance degradation • Feedback control is ROBUST (it is insensitive to plant changes, e. g. in gain and time constant) • Feedback control: “sudden” performance degradation (instability) Instability occurs if we over-react (loop gain is too large compared to effective time delay). • Feedback control: Changes system dynamics (eigenvalues) • Example was for single input - single output (SISO) case • Differences may be more striking in multivariable (MIMO) case 39

Feedback is an amazingly powerful tool 40

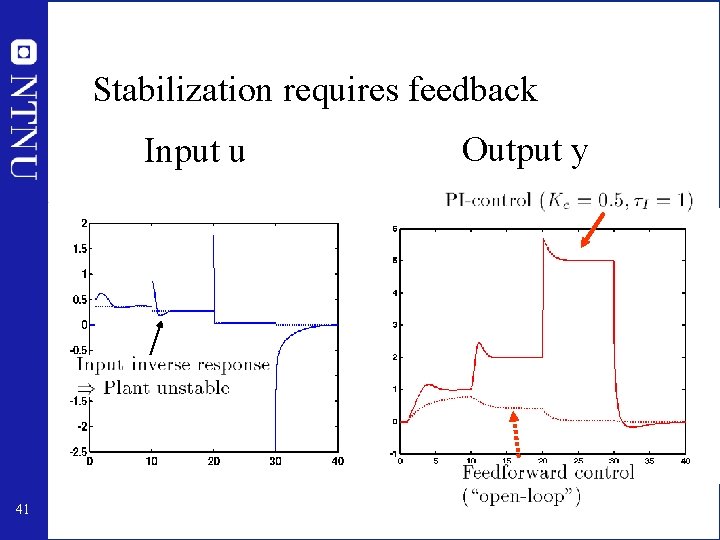
Stabilization requires feedback Input u 41 Output y

Conclusion: Why feedback? (and not feedforward control) • • • Simple: High gain feedback! Counteract unmeasured disturbances Reduce effect of changes / uncertainty (robustness) Change system dynamics (including stabilization) Linearize the behavior No explicit model required • MAIN PROBLEM • Can not have fast/tight control of plant with (effective) time delay • Potential instability (may occur “suddenly”) with time delay 42

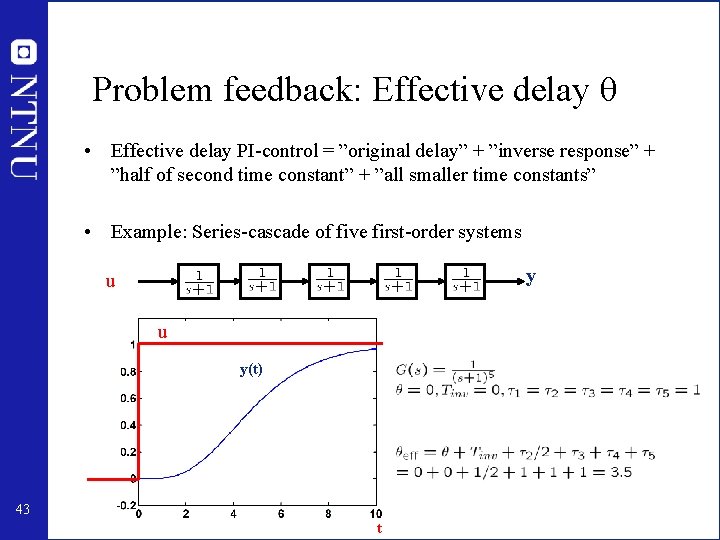
Problem feedback: Effective delay θ • Effective delay PI-control = ”original delay” + ”inverse response” + ”half of second time constant” + ”all smaller time constants” • Example: Series-cascade of five first-order systems y u u y(t) 43 t

PI-control with single measurement 44

Improve control? • Some improvement possible with more complex controller – – For example, add derivative action (PID-controller) May reduce θeff from 3. 5 s to 2. 5 s Problem: Sensitive to measurement noise Does not remove the fundamental limitation (recall waterbed) • Add extra measurement and introduce local control – May remove the fundamental waterbed limitation • Waterbed limitation does not apply to first-order system – Cascade 45

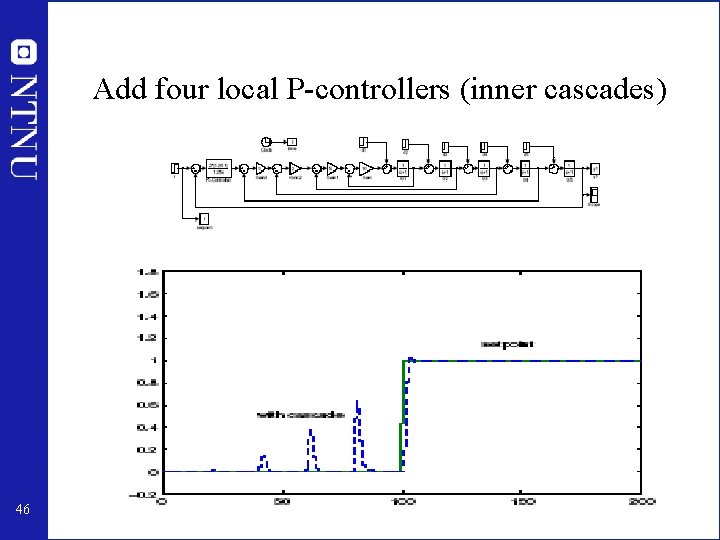
Add four local P-controllers (inner cascades) 46

CONTROL HIEARCHIES 47

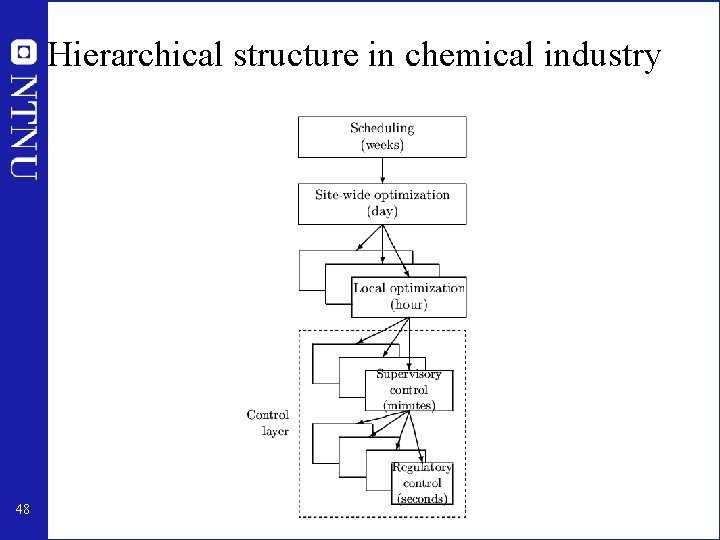
Hierarchical structure in chemical industry 48

Engineering systems • Most (all? ) large-scale engineering systems are controlled using hierarchies of quite simple single-loop controllers – Commercial aircraft – Large-scale chemical plant (refinery) • 1000’s of loops • Simple components: on-off + P-control + PI-control + nonlinear fixes + some feedforward Same in biological systems 49

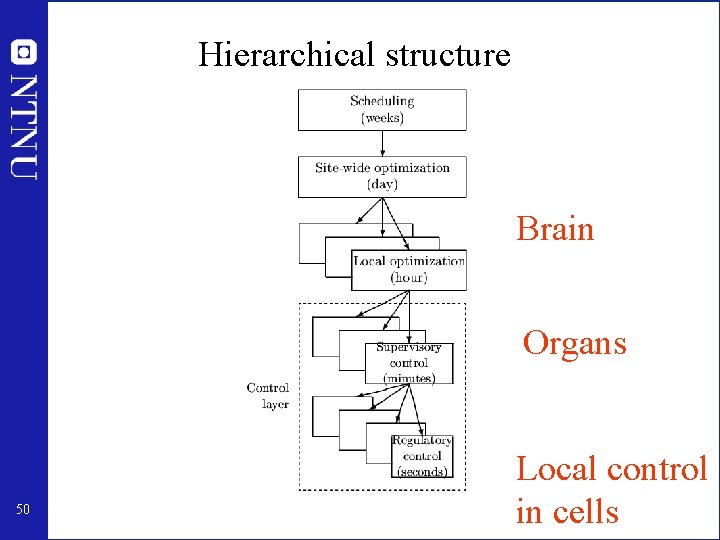
Hierarchical structure Brain Organs 50 Local control in cells

Alan Foss (“Critique of chemical process control theory”, AICh. E Journal, 1973): The central issue to be resolved. . . is the determination of control system structure. Which variables should be measured, which inputs should be manipulated and which links should be made between the two sets? 51

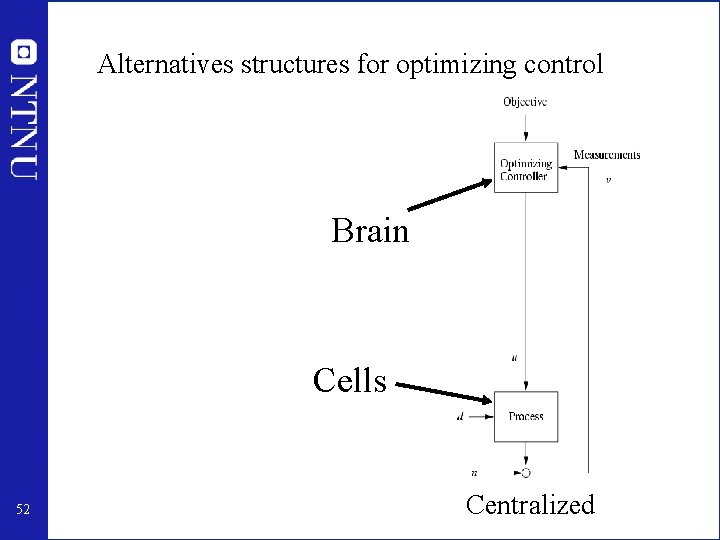
Alternatives structures for optimizing control What should we control? Brain Cells 52 Hierarchical Centralized

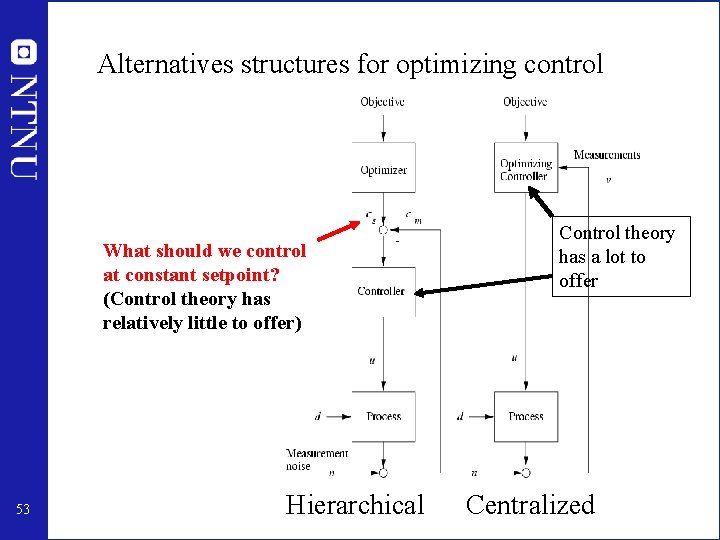
Alternatives structures for optimizing control What should we control at constant setpoint? (Control theory has relatively little to offer) 53 Hierarchical Control theory has a lot to offer Centralized

Self-optimizing Control – Marathon • Optimal operation of Marathon runner, J=T – Any self-optimizing variable c (to control at constant setpoint)? 54

Self-optimizing Control – Marathon • Optimal operation of Marathon runner, J=T – Any self-optimizing variable c (to control at constant setpoint)? • • 55 c 1 = distance to leader of race c 2 = speed c 3 = heart rate c 4 = level of lactate in muscles

Self-optimizing control (Skogestad, 2000) J = cost (overall objective to be minimized) Loss L = J - Jopt (d) Self-optimizing control is achieved when a constant setpoint policy results in an acceptable loss L (without the need to reoptimize when disturbances occur) 56

Good candidate controlled variables c (for self-optimizing control) Requirements: • The optimal value of c should be insensitive to disturbances • c should be easy to measure and control • The value of c should be sensitive to changes in the degrees of freedom (Equivalently, J as a function of c should be flat) • For cases with more than one unconstrained degrees of freedom, the selected controlled variables should be independent. Singular value rule (Skogestad and Postlethwaite, 1996): Look for variables that maximize the minimum singular value of the appropriately scaled steady-state gain matrix G from u to c 57

Biological systems • ”Self-optimizing” controlled variables have presumably been found by natural selection • Need to do ”reverse engineering” : – Find the controlled variables used in nature – From this identify what overall objective the biological system has been attempting to optimize 58

Conclusion • Negative Feedback is an extremely powerful tool • Complex systems can be controlled by hierarchies (cascades) of singleinput-single-output (SISO) control loops • Control extra local variables (secondary outputs) to avoid fundamental feedback control limitations • Control the right variables (primary outputs) to achieve ”selfoptimizing control” 59

Relationship to system biology: What can the control field contribute? • Advanced methods for model-based centralized controller design – Probably of minor interest in biological systems – Unlikely that nature has developed many multivariable control solutions • Understanding of feedback systems – – • Analysis tools Robustness Cascade control Same inherent limitations apply in biological systems Understanding and design of hierarchical control systems – Important both in engineering and biological systems – BUT: Underdeveloped area in control • ”Large scale control systems community”: Out of touch with reality 60