Control Theory Control System Objectives m Establish a

Control Theory Control System Objectives m Establish a final condition m Provide safe operation m Eliminate the human element m Assure economical operation

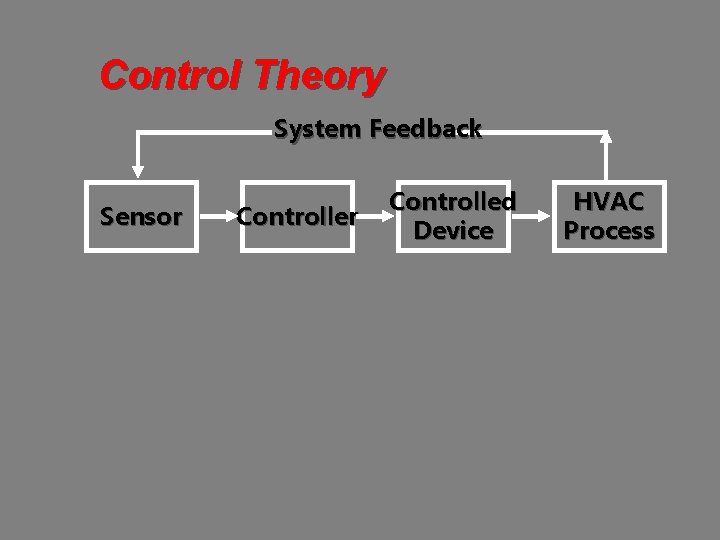
Control Theory System Feedback Sensor Controlled Device HVAC Process

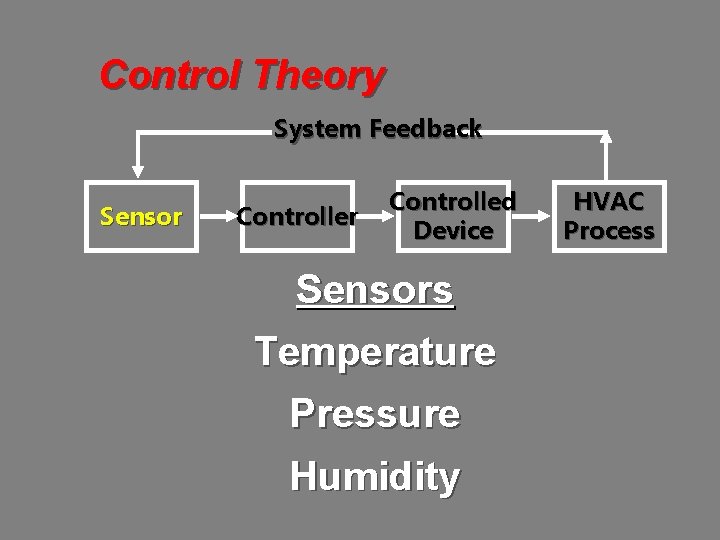
Control Theory System Feedback Sensor Controlled Device Sensors Temperature Pressure Humidity HVAC Process

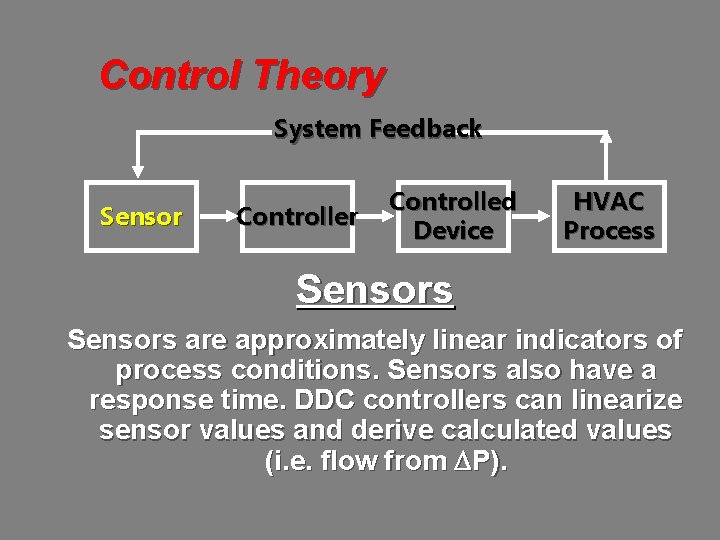
Control Theory System Feedback Sensor Controlled Device HVAC Process Sensors are approximately linear indicators of process conditions. Sensors also have a response time. DDC controllers can linearize sensor values and derive calculated values (i. e. flow from P).

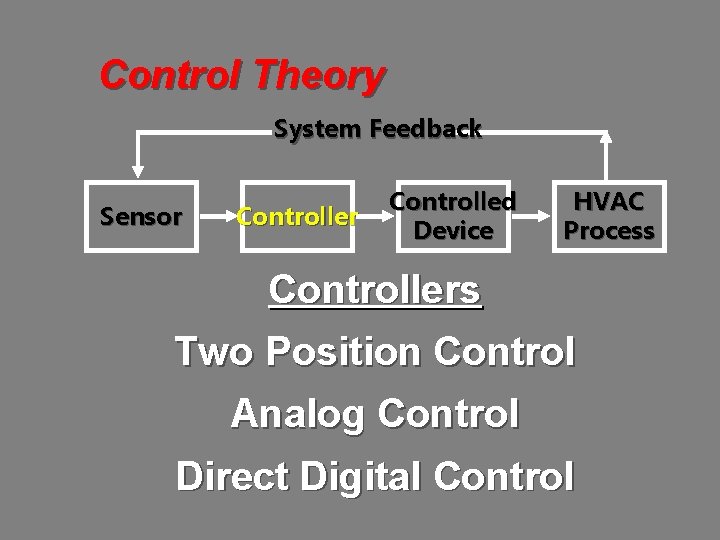
Control Theory System Feedback Sensor Controlled Device HVAC Process Controllers Two Position Control Analog Control Direct Digital Control

Control Theory Two Position Control Typically a mechanical device such as a thermostat or pressure switch Picture of A 70

Control Theory Two Position Control A mechanical thermostat opens or closes a relay based on the temperature. this applies a voltage to a two position fan coil valve which goes full open or full closed. Differential Cut out temperature No flow to FCU Temperature Increasing Cut in temperature Full flow to FCU

Control Theory Two Position Control Low Cost Inaccurate Control Inflexible Strategies Cannot be Networked Used for Simple On / Off Control such as FCU in Hotel Guest Rooms Used for Safety Controls

Control Theory Analog Control Uses analog electronics but no microprocessor. Picture of System 350

Control Theory Analog Control A temperature sensor located in the return air of a CAV AHU controls the chilled water valve using a proportional algorithm.

Control Theory Analog Control Low-Medium Cost Reasonably Accurate Control Inflexible Strategies Cannot be Networked Used for AHU without BAS

Control Theory Direct Digital Control Uses microprocessor to do calculations and can be networked with BAS Picture of DDC Controller

Control Theory Direct Digital Control 1. Convert input signal from analog to digital format 2. Use computer program to calculate the value to be sent to the output 3. Generate output signal from calculated value

Control Theory Direct Digital Control Medium Cost Accurate Control Flexible Strategies Can be Networked Used for AHU with BAS

Control Theory Direct Digital Control Current DDC technology implements analog control algorithms using microprocessor. Next generation DDC technology will add adaptive tuning, mechanical system diagnostics and characterization of the controlled device.

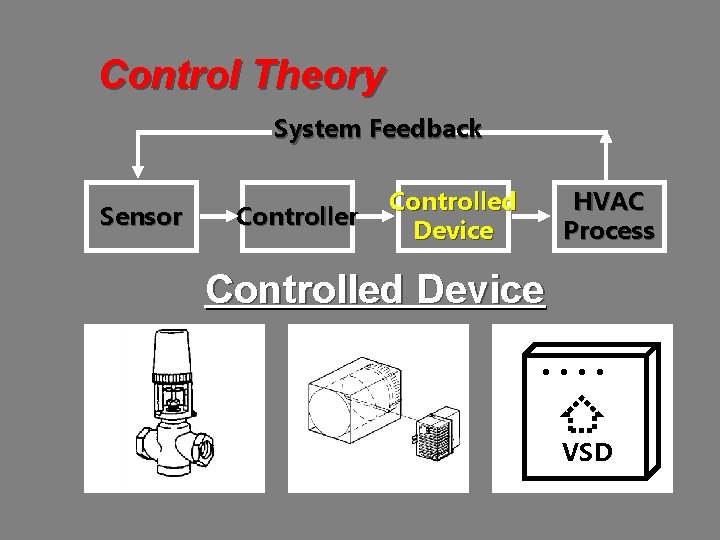
Control Theory System Feedback Sensor Controlled Device HVAC Process Controlled Device VAV Box Actuator VSD

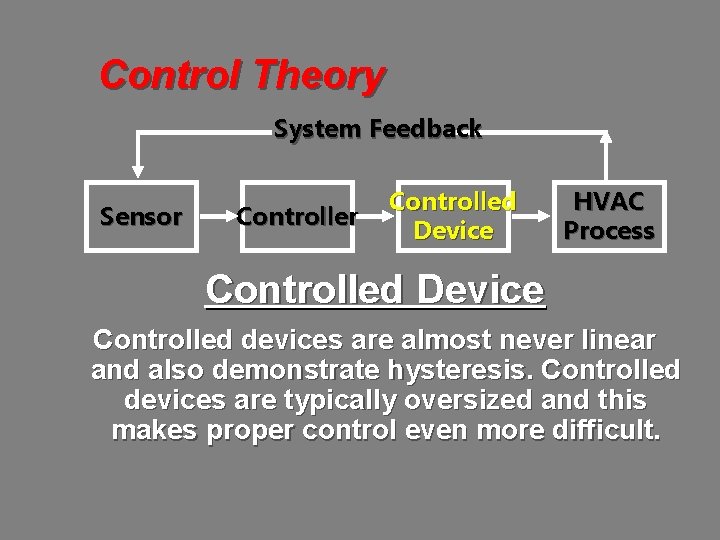
Control Theory System Feedback Sensor Controlled Device HVAC Process Controlled Device Controlled devices are almost never linear and also demonstrate hysteresis. Controlled devices are typically oversized and this makes proper control even more difficult.

Control Theory System Feedback Sensor Controlled Device HVAC Process It is critical to understand the characteristics of the HVAC process when applying controls.

Control Theory System Feedback Sensor Controlled Device HVAC Process The HVAC process will limit the range of possible control. For example, the mechanical system will not allow a room setpoint of 5°C to be achieved.

Control Theory System Feedback Sensor Controlled Device HVAC Process System Feedback The system feedback will introduce delays. For example, it may take a few minutes for a change in valve position to cause a change in room temperature.

Control Theory System Feedback Sensor Controlled Device HVAC Process System Feedback The system feedback will introduce “noise”. For example, turbulence and stratification make accurate measure of pressure and temperature difficult.

Control Theory System Feedback Sensor Controlled Device HVAC Process Examples of VAV Control Loops

Control Theory. Air stream after cooling coil affects temperature sensor System Feedback Sensor Controlled Device HVAC Process Temperature DDC Valve actuator. Cooling coil sensor located Controller and chilled extracts heat after cooling coil water valvefrom air stream Off-Coil Temperature Control in VAV AHU

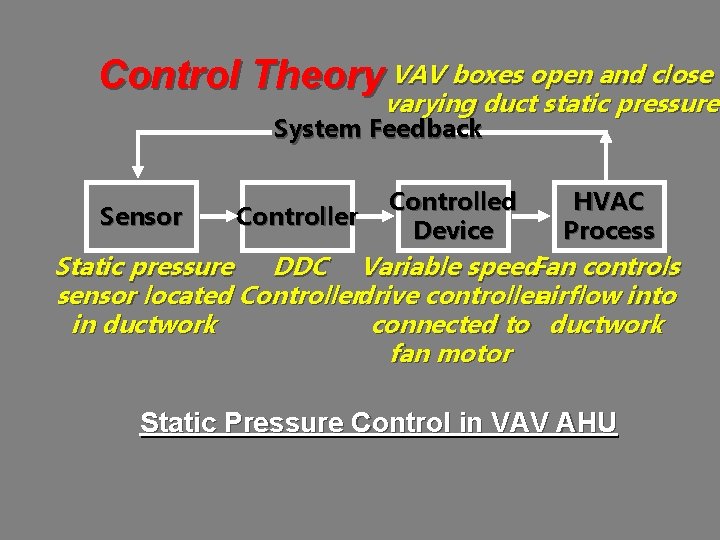
Control Theory VAV boxes open and close varying duct static pressure System Feedback Sensor Controlled Device HVAC Process Static pressure DDC Variable speed. Fan controls sensor located Controllerdrive controllerairflow into in ductwork connected to ductwork fan motor Static Pressure Control in VAV AHU

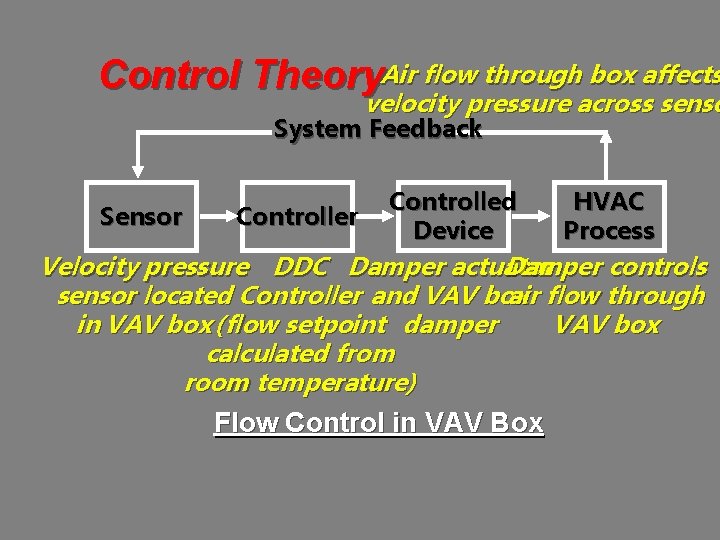
Control Theory. Air flow through box affects velocity pressure across senso System Feedback Sensor Controlled Device HVAC Process Velocity pressure DDC Damper actuator Damper controls sensor located Controller and VAV box air flow through in VAV box (flow setpoint damper VAV box calculated from room temperature) Flow Control in VAV Box

Control Theory Control Loop Calculations

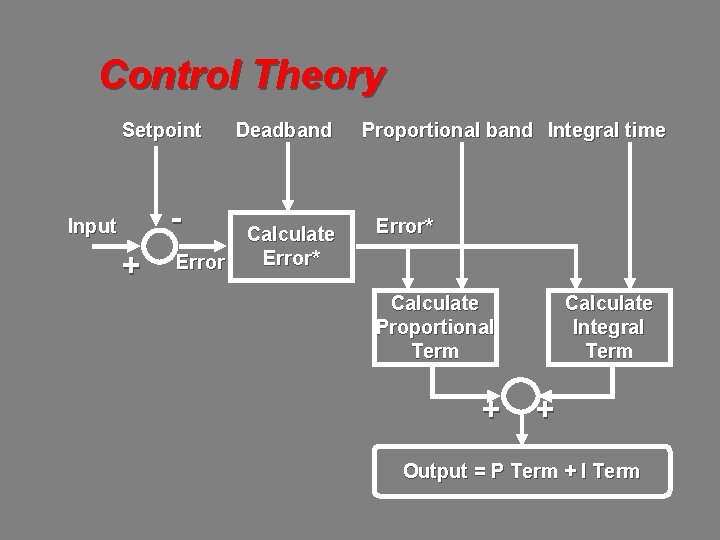
Control Theory Setpoint - Input + Error Deadband Calculate Error* Proportional band Integral time Error* Calculate Proportional Term + Calculate Integral Term + Output = P Term + I Term

Control Theory Control Loop Calculations The first step is to calculate the difference between the controlled variable (input) and the setpoint. This difference is called “Error”. Error = Input - Setpoint

Control Theory Control Loop Calculations If Error is less than the Deadband, then Error* = 0 If Error is greater than the Deadband, then Error* = Error - Deadband If Input is close to Setpoint (± Deadband), then assume Error is zero. The use of a Deadband eliminates minor output adjustments and stabilizes control.

Control Theory Control Loop Calculations Next, calculate the Proportional Term: For Proportional-Only control: Output = Proportional Term

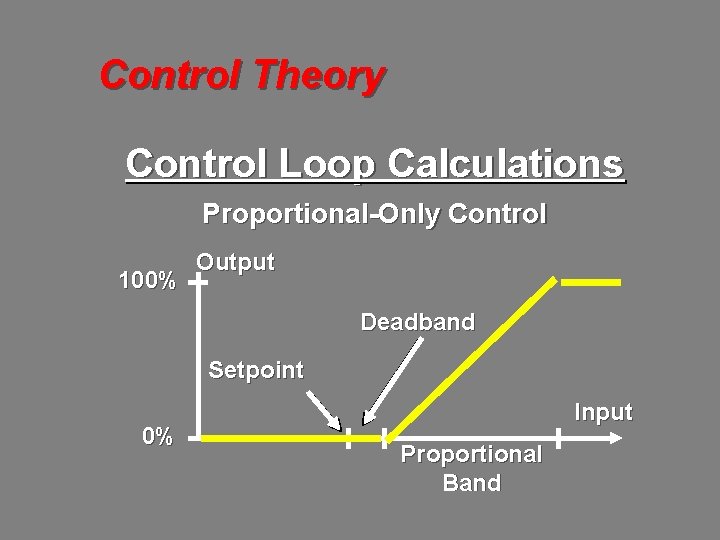
Control Theory Control Loop Calculations Proportional-Only Control 100% Output Deadband Setpoint 0% Input Proportional Band

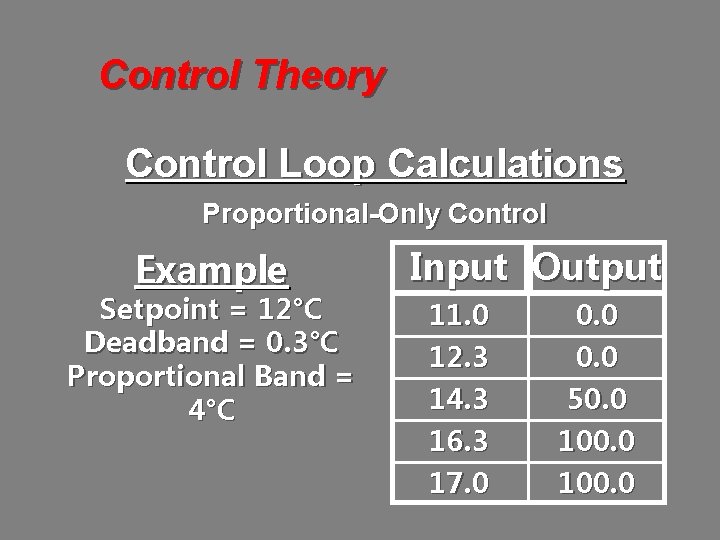
Control Theory Control Loop Calculations Proportional-Only Control Example Setpoint = 12°C Deadband = 0. 3°C Proportional Band = 4°C Input Output 11. 0 12. 3 14. 3 16. 3 17. 0 0. 0 50. 0 100. 0

Control Theory Control Loop Calculations In the DDC Controller, the control loop calculations are repeated every 1. 5 seconds. A new sample of the input and a new output command is calculated every 1. 5 seconds. The Proportional Term is not time dependent. The Proportional Term is calculated each 1. 5 seconds and the calculation does not depend on previous calculations.

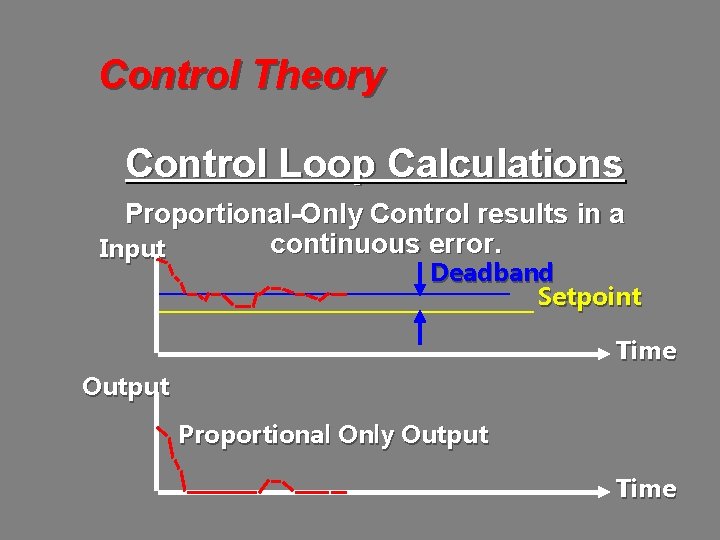
Control Theory Control Loop Calculations Proportional-Only Control results in a continuous error. Input Deadband Setpoint Time Output Proportional Only Output Time

Control Theory Control Loop Calculations The Integral Term is time dependent: Integral Term as calculated at this sample time Proportional Term Integral Term as calculated at this sample at the previous time sample time

Control Theory Control Loop Calculations The Integral Term will be calculated as long as the output is between 0% and 100%. Once the output is 0% or 100%, the Integral Term will stop calculating. This feature is called “anti-windup”. Anti-windup allows the loop to change from saturation to control as quickly as possible.

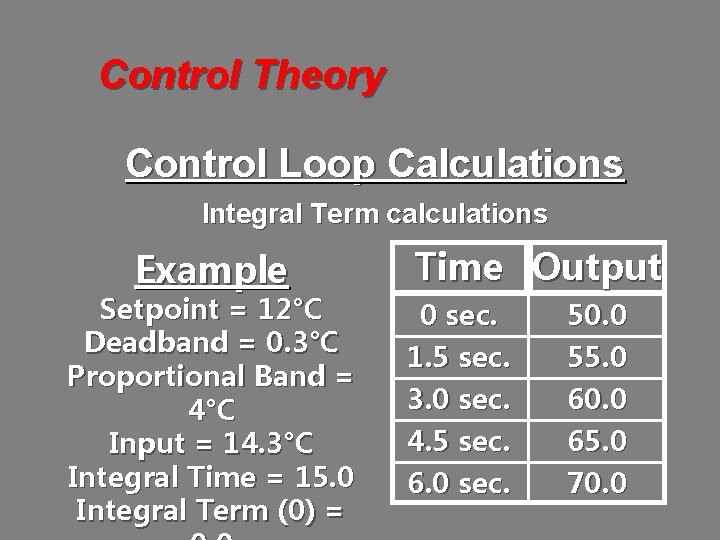
Control Theory Control Loop Calculations Integral Term calculations Example Setpoint = 12°C Deadband = 0. 3°C Proportional Band = 4°C Input = 14. 3°C Integral Time = 15. 0 Integral Term (0) = Time Output 0 sec. 1. 5 sec. 3. 0 sec. 4. 5 sec. 6. 0 sec. 50. 0 55. 0 60. 0 65. 0 70. 0

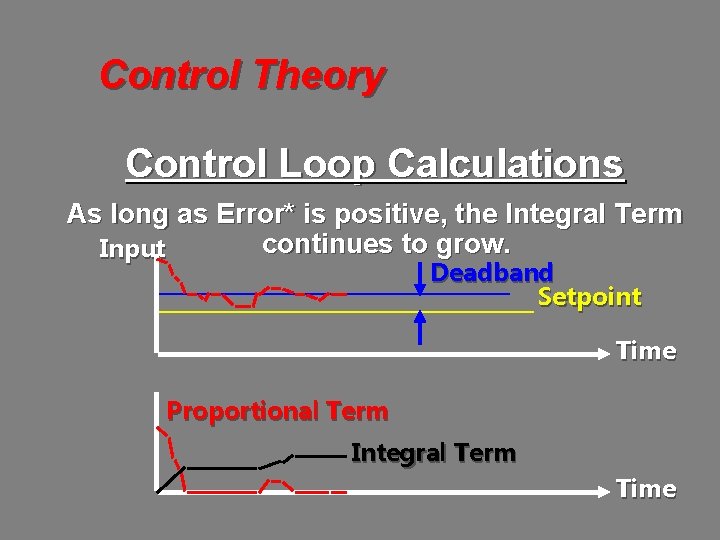
Control Theory Control Loop Calculations As long as Error* is positive, the Integral Term continues to grow. Input Deadband Setpoint Time Proportional Term Integral Term Time

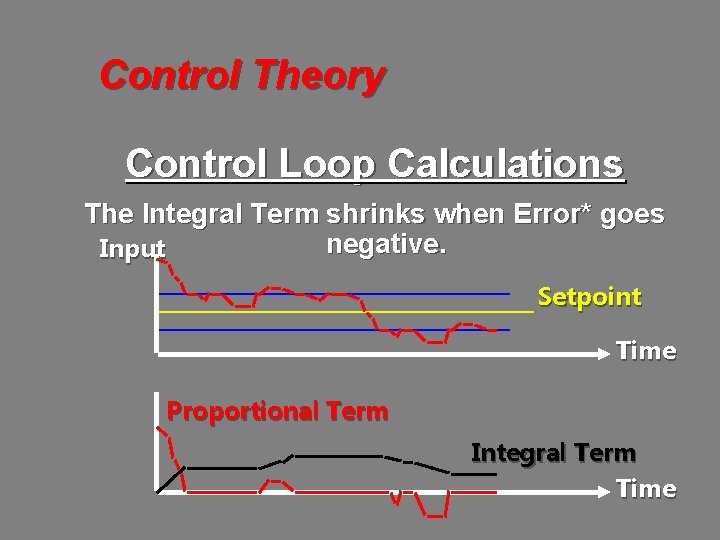
Control Theory Control Loop Calculations The Integral Term shrinks when Error* goes negative. Input Setpoint Time Proportional Term Integral Term Time

Control Theory Control Loop Calculations The output of a proportional plus integral control loop will force the error to zero over time. Most HVAC applications use proportional plus integral control loops. Output Integral Term Proportional Term Time

Control Theory Control Loop Calculations The proportional term affects the sensitivity of the control loop. (STRENGTH) The integral term affects the responsiveness of the control loop. (SPEED)

Control Theory Control Loop Calculations DDC Controllers are equipped to provide Proportional + Integral + Derivative control but the derivative term is almost never used. The derivative term is proportional to the rate of change of the input. The derivative term “amplifies” any naturally occurring “noise” in the input resulting in unstable control.