Control Systems for Application in Robotics Dara Kusic

Control Systems for Application in Robotics Dara Kusic Department of Computer Science University of Pittsburgh, PA 15260 Honors Robotics February 8, 2010 Department of Computer Science, University of Pittsburgh

OUTLINE u Control problems in robotics u Centralized, single robot control – Open-loop & closed-loop (feedback) control – Model predictive control u Decentralized, u Advanced multiple robot control topcis – Machine learning and adaptive control Department of Computer Science, University of Pittsburgh 2

Control problems in robotics u. Localization -- how does a mobile robot know where it is? u. Navigation – how does a mobile robot reach its destination? u. Actuation – how does the robot manuver its end effector to make contact with a target? u. Coordination – how to robot swarms cooperate to solve a common task? Department of Computer Science, University of Pittsburgh 3

Common control objectives u. Tracking -- e. g. maintain a specified distance from a moving target u. Disturbance rejection – e. g. maintain deadreckoning mode under windy conditions u. Optimization – e. g. deliver the daily mail to cubicles in the shortest path possible Department of Computer Science, University of Pittsburgh 4

OUTLINE u Control problems in robotics u Centralized, single robot control – Open-loop & closed-loop (feedback) control – Model predictive control u Decentralized, u Advanced multiple robot control topcis – Machine learning and adaptive control Department of Computer Science, University of Pittsburgh 5

Single robot open-loop control u Control input is computed only from current state and a model of the system – The use of odometry is an example of open loop control, where the robot position is estimated via data from velocity actuators, integrated over time Advantage: Simple to use – requires no data from sensors to be integrated in the control scheme u Disadvantage: Error-prone due to inaccuracies in system model and environmental disturbances u – Open-loop control does not have the capacity for error-correction disturbance noise setpoint controller signal system output Department of Computer Science, University of Pittsburgh 6

Closed-loop or feedback control u Control input is computed from current state and measurements of an observable output of the system – Automobile cruise control is a typical example of feedback control, where acceleration or deceleration is updated using the error from the desired velocity from the actual velocity Advantage: More accurate than open-loop control particularly in uncertain operating conditions; no model requried u Disadvantage: More costly due to the use of measurement instrumentation and sensors; noisy data disturbance noise u setpoint error controller signal system output observed value Department of Computer Science, University of Pittsburgh 7

Feedback control in discrete systems u. Robotic systems will typically operate in the discrete domain u. Design choices of sampling time must be carefully considered – At what frequency to sample system output? – At which frequency to deliver control input? » Which frequency should be smaller? Department of Computer Science, University of Pittsburgh 8

On-off feedback ontrol u For example, a thermostat, when the heater is either on or off u Depending on the frequency of control, overhead of on-off, etc, this could cause overshoots and undershoots (ripples) – Oscillation is a common behavior in control systems – Hysteresis may be unacceptable in the system: e. g. To maintain a temperature of 20 °C, one might set a thermostat to turn on the furnace when the temperature drops below 18 °C, and turn it off when the temperature exceeds 22 °C. If the temperature is 21 °C, then it is not possible to predict whether the furnace is on or off without knowing the history of the temperature. Department of Computer Science, University of Pittsburgh 9

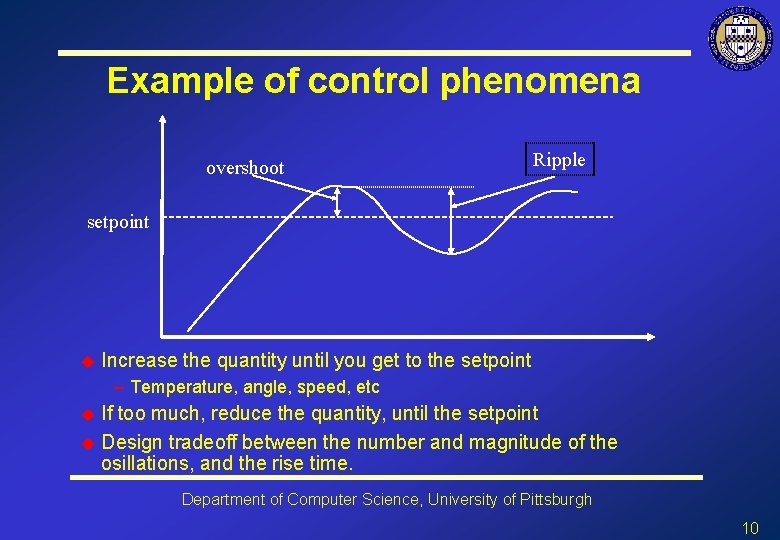
Example of control phenomena overshoot Ripple setpoint u Increase the quantity until you get to the setpoint – Temperature, angle, speed, etc If too much, reduce the quantity, until the setpoint u Design tradeoff between the number and magnitude of the osillations, and the rise time. u Department of Computer Science, University of Pittsburgh 10

Control properties u. Stability – for any bounded input, the output of the system is also bounded u. Accuracy – the proximity of the measured output of the system to its desired operating point in its steady-state u. Overshoot – how far the control input causes the system to overreach its operating point u. Rise time – the time to respond to a disturbance or change in setpoint u. Settlng time – the time to converge to the desired operating point Department of Computer Science, University of Pittsburgh 11

PID feedback control u. Proportional-Integral-Derivative control – Proportional value reacts to the current error between the desired setpoint and the measured quantity – Integral value reacts to the cumulative error – Derivative value reacts to the recent change in the error u. May implement only P control, I control, D control, or any combination therein u. Each type of control, acting independently, will exhibit different behaviors and limitations Department of Computer Science, University of Pittsburgh 12

PID feedback ontrol u. The discrete form of PID control can be represented by the following: Department of Computer Science, University of Pittsburgh 13

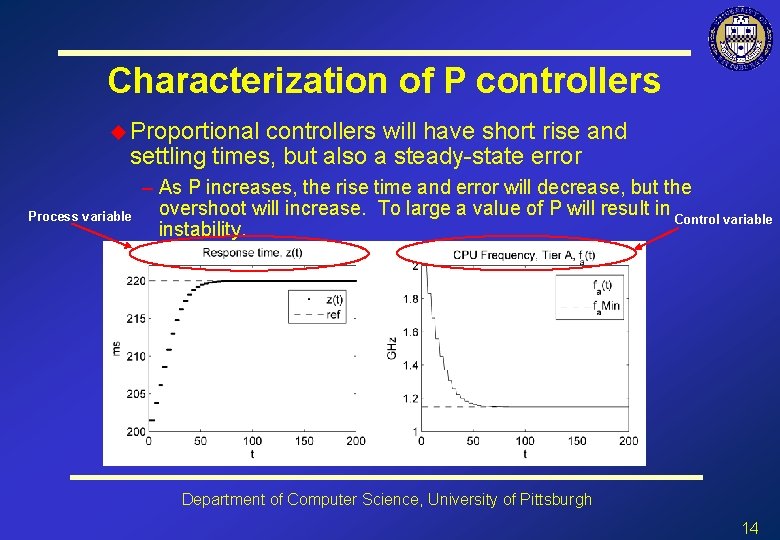
Characterization of P controllers u Proportional controllers will have short rise and settling times, but also a steady-state error Process variable – As P increases, the rise time and error will decrease, but the overshoot will increase. To large a value of P will result in Control variable instability. Department of Computer Science, University of Pittsburgh 14

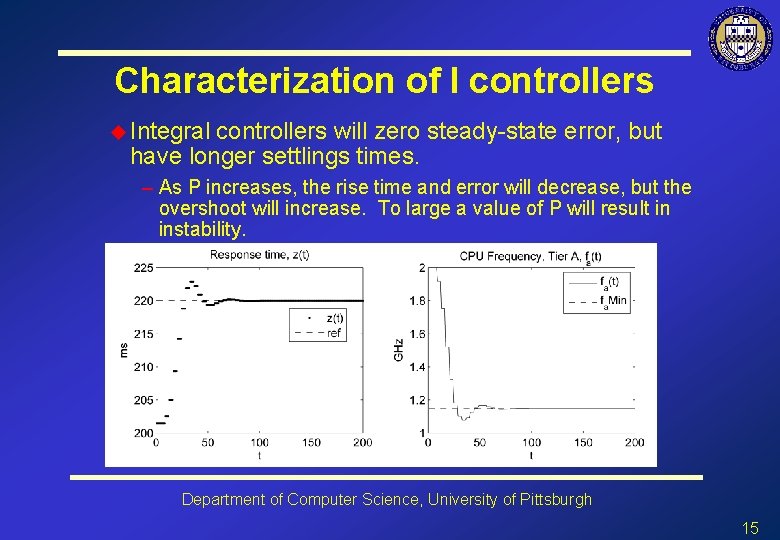
Characterization of I controllers u Integral controllers will zero steady-state error, but have longer settlings times. – As P increases, the rise time and error will decrease, but the overshoot will increase. To large a value of P will result in instability. Department of Computer Science, University of Pittsburgh 15

Characterization of D controllers u Derivative can reduce oscillations but add to the settling time. – Typically, D controllers are used for gradual control in longrunning processes such as thermal or chemical. Department of Computer Science, University of Pittsburgh 16

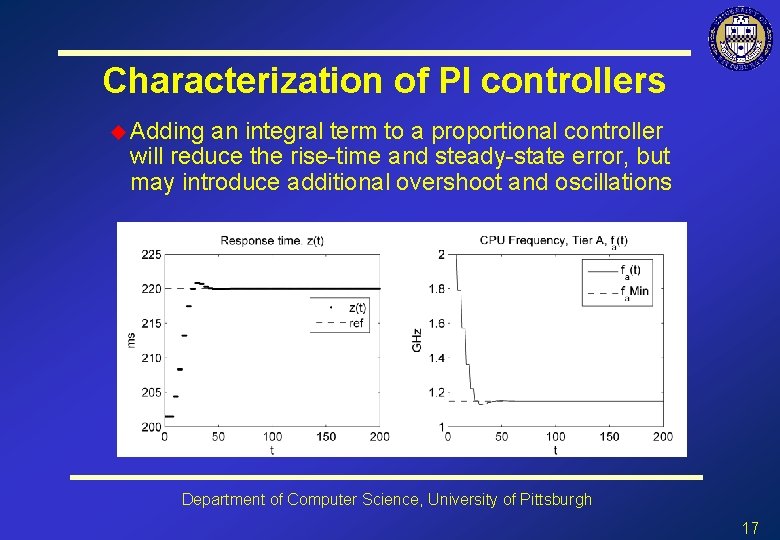
Characterization of PI controllers u Adding an integral term to a proportional controller will reduce the rise-time and steady-state error, but may introduce additional overshoot and oscillations Department of Computer Science, University of Pittsburgh 17

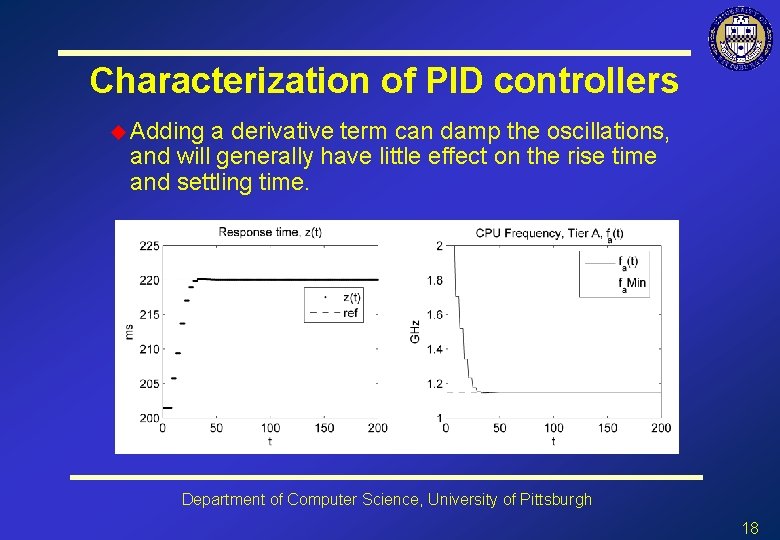
Characterization of PID controllers u Adding a derivative term can damp the oscillations, and will generally have little effect on the rise time and settling time. Department of Computer Science, University of Pittsburgh 18

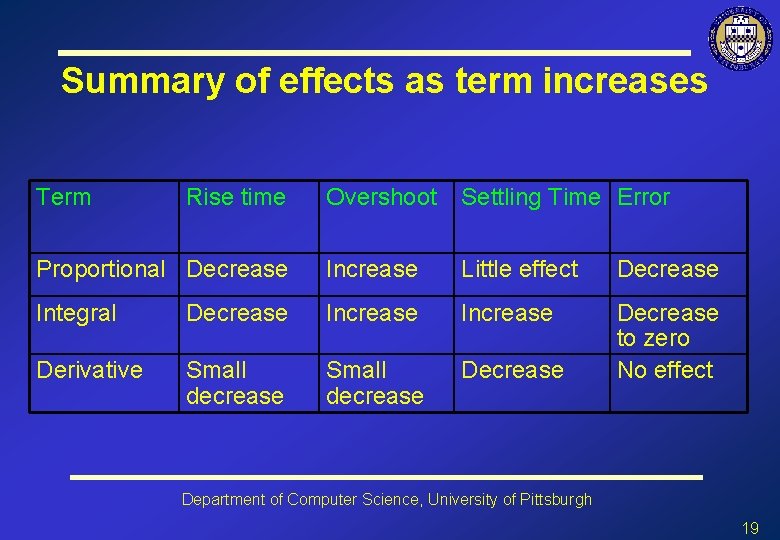
Summary of effects as term increases Term Rise time Overshoot Settling Time Error Proportional Decrease Increase Little effect Decrease Integral Decrease Increase Derivative Small decrease Decrease to zero No effect Department of Computer Science, University of Pittsburgh 19

PID tuning u In a real system, PID tuning can be something of an art – Overhoot thresholds – Oscillation tolerance – Rise time constraints u There are, however, some ‘rules of thumb’ for initial values (as applied to the ideal parallel form presented herein) u Start with the integral and derivative terms set to zero, then add integral until error is zero, and deriative until oscillations decrease Department of Computer Science, University of Pittsburgh 20

Cascading control u Cascading control is when one controller, an outer, or primary controller, controls an inner, or secondary controller. The cascade can continue recursively to the nth inner controller. – Cascading control is implemented when a process with slow dynamics, such as temperature in a large tank, is influenced by a process with fast dynamics, such as the flow rate of hot water into the tank. The primary controller will determine the setpoint for the secondary controller. For example, if the primary controller wishes to raise the tank temperature to 100 Celcius, it will determine a setpoint for the flow rate of steam into the tank. The secondary controller will regulate the valve position to maintain that setpoint. – In robotics, a primary controller might wish to maintain a constant velocity by determining a setpoint acceleration for a secondary controller. The secondary controller will track that acceleration by modulating the pulse rate to the motors. Department of Computer Science, University of Pittsburgh 21

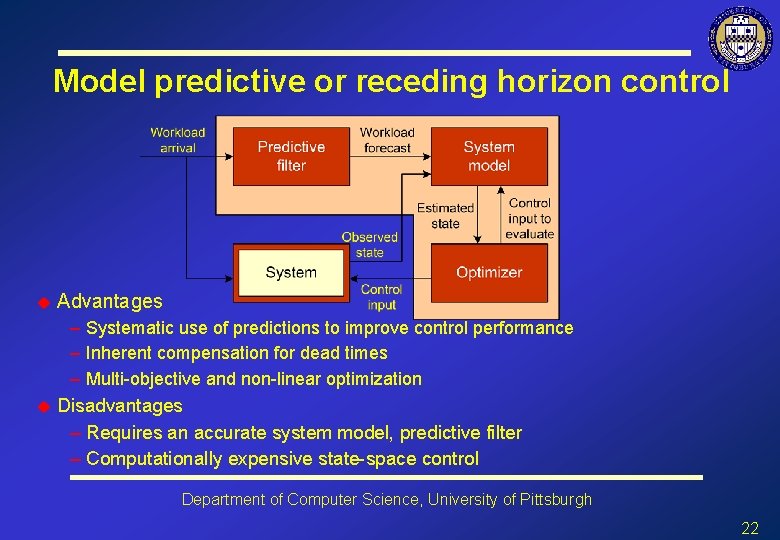
Model predictive or receding horizon control u u Advantages – Systematic use of predictions to improve control performance – Inherent compensation for dead times – Multi-objective and non-linear optimization Disadvantages – Requires an accurate system model, predictive filter – Computationally expensive state-space control Department of Computer Science, University of Pittsburgh 22

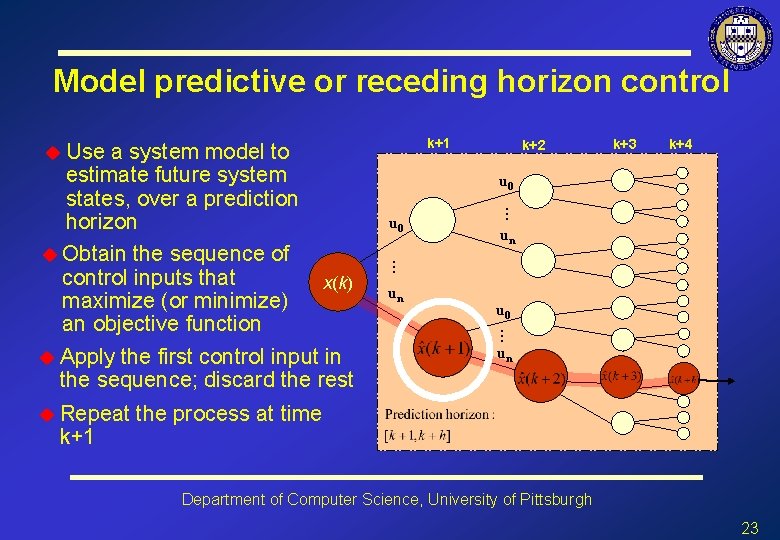
Model predictive or receding horizon control u 0 x(k) un un u 0 … k+1 k+4 u 0 the first control input in the sequence; discard the rest u Repeat k+3 … u Apply k+2 … a system model to estimate future system states, over a prediction horizon u Obtain the sequence of control inputs that maximize (or minimize) an objective function k+1 u Use un the process at time Department of Computer Science, University of Pittsburgh 23

Statistical filtering u Measurement data may be noisy with statistical variations – Should the robot react to every perceived disturbance? u Statistical filters can smooth noisy data – Exponentially weighted moving averages – Adjusted averages for weighted standard deviation – Outlier rejection (low-pass filtering) Department of Computer Science, University of Pittsburgh 24

OUTLINE u Control problems in robotics u Centralized, single robot control – Open-loop & closed-loop (feedback) control – Model predictive control u Decentralized, u Advanced multiple robot control topcis – Machine learning and adaptive control Department of Computer Science, University of Pittsburgh 25

Fully decentralized, multi-robot control u Multiple robots may need to cooperate to achieve a common goal, e. g. Take possession of a soccer ball and attempt to score – What would happen if all the robots simultaneously sought after the goal? – Cell phone transmission protocols such as CSMA can provide inspiration for disbursing actions (e. g. via exponentially weighted action timers) u Distributed and decentralized control algorithms are typically used for coordination tasks – Implicit communication via global data objects – Explicit communication via unicast, multicast, or broadcast in order of increasing bandwidth. Forwarding of messages can occur by default, or by some more conservative algorithm such as gossip Department of Computer Science, University of Pittsburgh 26

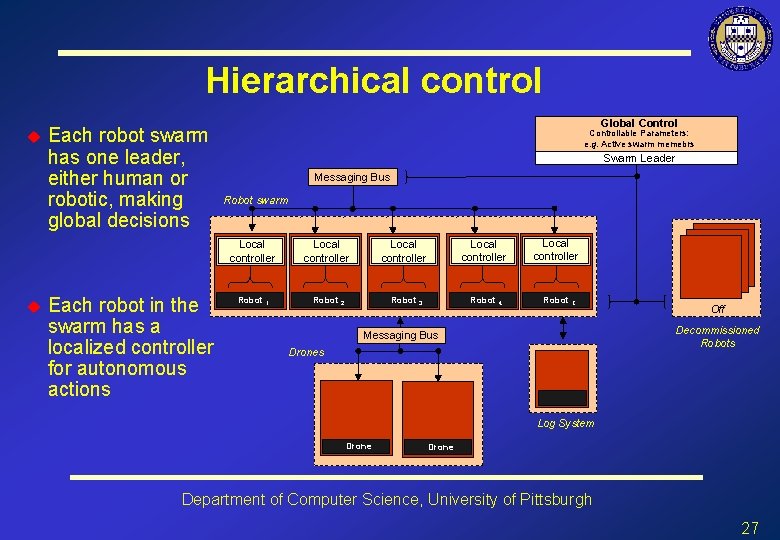
Hierarchical control u u Each robot swarm has one leader, either human or robotic, making global decisions Each robot in the swarm has a localized controller for autonomous actions Global Controllable Parameters: e. g. Active swarm memebrs Swarm Leader Messaging Bus Robot swarm Local controller Robot 1 Robot 2 Robot 3 Robot 4 Local controller Robot C Off Decommissioned Robots Messaging Bus Drones Log System Drone Department of Computer Science, University of Pittsburgh 27

OUTLINE u Control problems in robotics u Centralized, single robot control – Open-loop & closed-loop (feedback) control – Model predictive control u Decentralized, u Advanced multiple robot control topcis – Machine learning and adaptive control Department of Computer Science, University of Pittsburgh 28

Machine learning u Conrtrols with high computational demand or unidentified systems can benefit from machine learning algorithms – Neural networks » Require discretiziation as output is continuous – Regression trees » Compared to NN, large storage requirement, but faster execution – Bayesian networks – Reinforcement learning u The basic approach is to simulate the system under a range of conditions, and collect the data for training the approximation structure u Approximating structures can be applied to as a system model, or as the controller itself Department of Computer Science, University of Pittsburgh 29

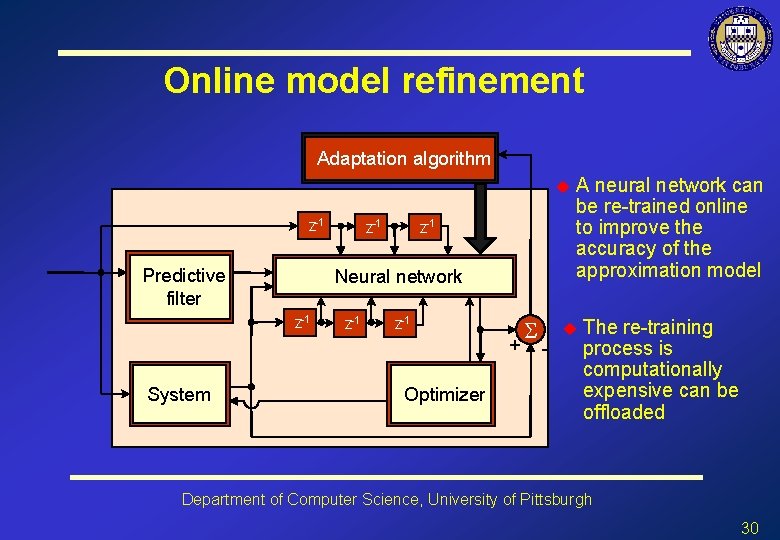
Online model refinement Adaptation System algorithm u z-1 Predictive System filter z-1 Neural System network z-1 z-1 + System Optimizer System S A neural network can be re-trained online to improve the accuracy of the approximation model u - The re-training process is computationally expensive can be offloaded Department of Computer Science, University of Pittsburgh 30

Taxonomy of fault handling System Reliability Redundant systems Non-redundant systems Fault avoidance Fault detection Fault-tolerant systems Dyamic redundancy Masking redundancy Online detection/masking Reconfig. Retry Repair Department of Computer Science, University of Pittsburgh 31

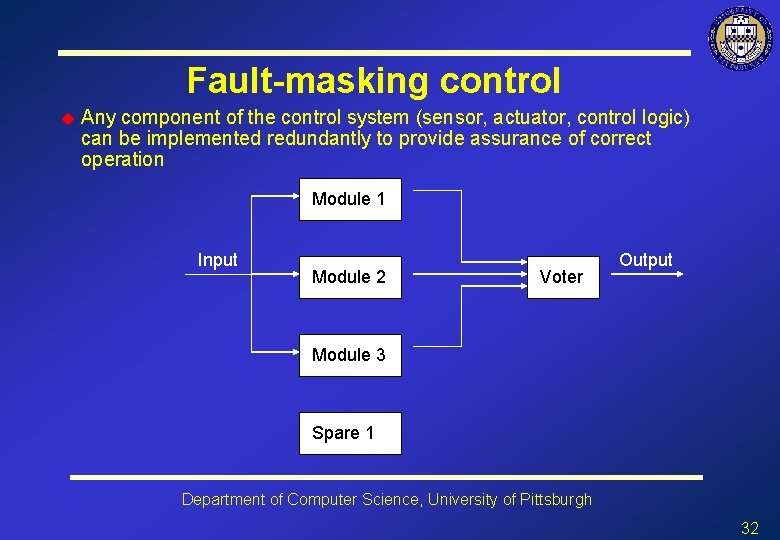
Fault-masking control u Any component of the control system (sensor, actuator, control logic) can be implemented redundantly to provide assurance of correct operation Module 1 Input Module 2 Voter Output Module 3 Spare 1 Department of Computer Science, University of Pittsburgh 32

Additional resources u Feedback control: – HELLERSTEIN, J. L. , DIAO, Y. , PAREKH, S. , AND TILBURY, D. M. Feedback Control of Computing Systems. Wiley-IEEE Press, 2004. u Neural networks: – HAYKIN, S. Neural Networks: A Comprehensive Foundation. Prentice-Hall, 1999. u Fault-tolerant systems: – STOREY, N. Safety-critical Computing Systems. Addison-Wesley, 1996. Department of Computer Science, University of Pittsburgh 33