Control Systems CS Lecture3 Introduction to Mathematical Modeling

Control Systems (CS) Lecture-3 Introduction to Mathematical Modeling & Mathematical Modeling of Electrical Systems Dr. Imtiaz Hussain Associate Professor Mehran University of Engineering & Technology Jamshoro, Pakistan email: imtiaz. hussain@faculty. muet. edu. pk URL : http: //imtiazhussainkalwar. weebly. com/ 1

Types of Systems • • Static System: If a system does not change with time, it is called a static system. Dynamic System: If a system changes with time, it is called a dynamic system. 2

Dynamic Systems • A system is said to be dynamic if its current output may depend on the past history as well as the present values of the input variables. • Mathematically, Example: A moving mass y u Model: Force=Mass x Acceleration M

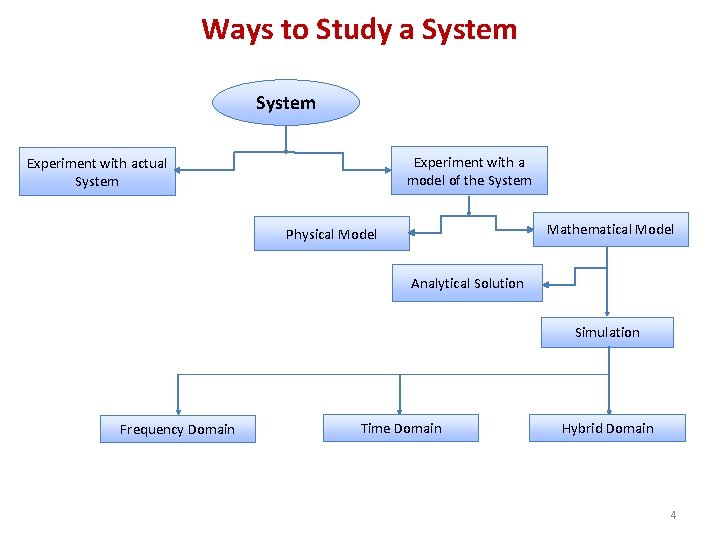
Ways to Study a System Experiment with a model of the System Experiment with actual System Mathematical Model Physical Model Analytical Solution Simulation Frequency Domain Time Domain Hybrid Domain 4

Model • • • A model is a simplified representation or abstraction of reality. Reality is generally too complex to copy exactly. Much of the complexity is actually irrelevant in problem solving. 5

What is Mathematical Model? A set of mathematical equations (e. g. , differential eqs. ) that describes the input-output behavior of a system. What is a model used for? • Simulation • Prediction/Forecasting • Prognostics/Diagnostics • Design/Performance Evaluation • Control System Design

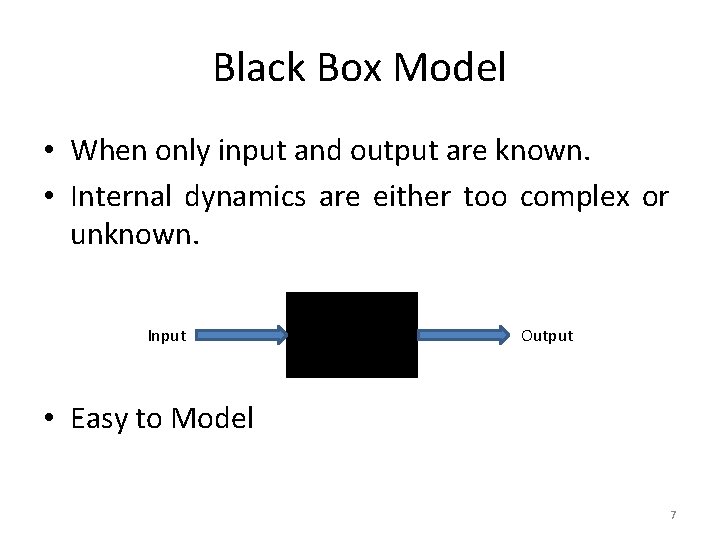
Black Box Model • When only input and output are known. • Internal dynamics are either too complex or unknown. Input Output • Easy to Model 7

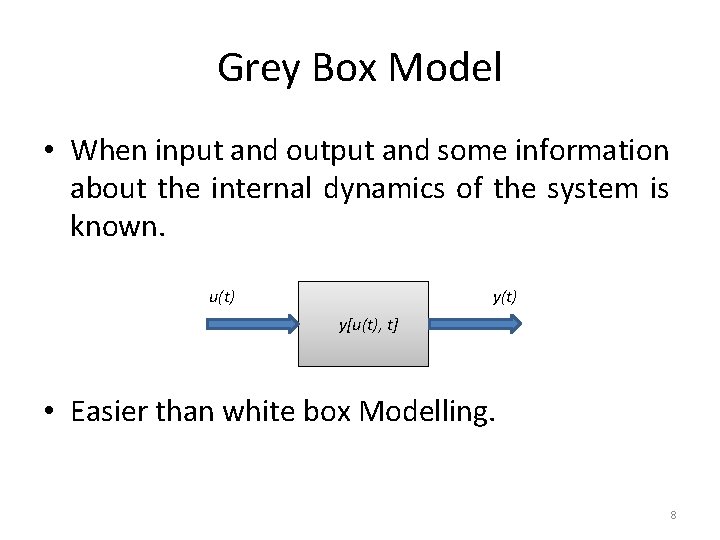
Grey Box Model • When input and output and some information about the internal dynamics of the system is known. u(t) y[u(t), t] • Easier than white box Modelling. 8

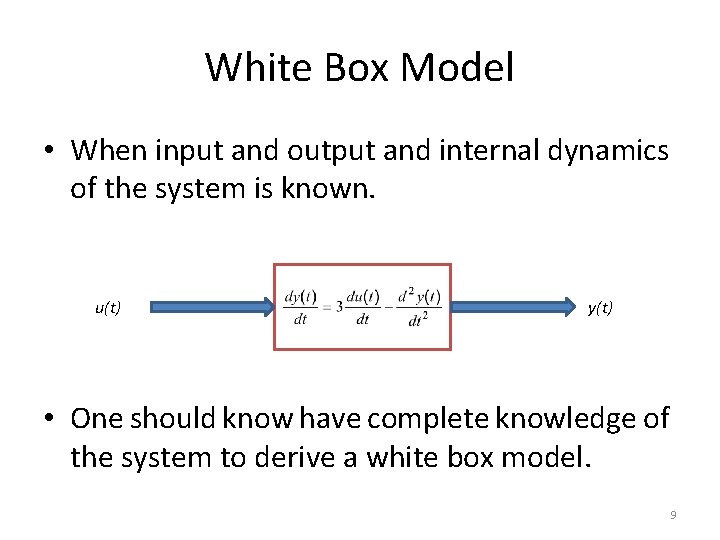
White Box Model • When input and output and internal dynamics of the system is known. u(t) y(t) • One should know have complete knowledge of the system to derive a white box model. 9

Basic Elements of Electrical Systems • The time domain expression relating voltage and current for the resistor is given by Ohm’s law i-e • The Laplace transform of the above equation is

Basic Elements of Electrical Systems • The time domain expression relating voltage and current for the Capacitor is given as: • The Laplace transform of the above equation (assuming there is no charge stored in the capacitor) is

Basic Elements of Electrical Systems • The time domain expression relating voltage and current for the inductor is given as: • The Laplace transform of the above equation (assuming there is no energy stored in inductor) is

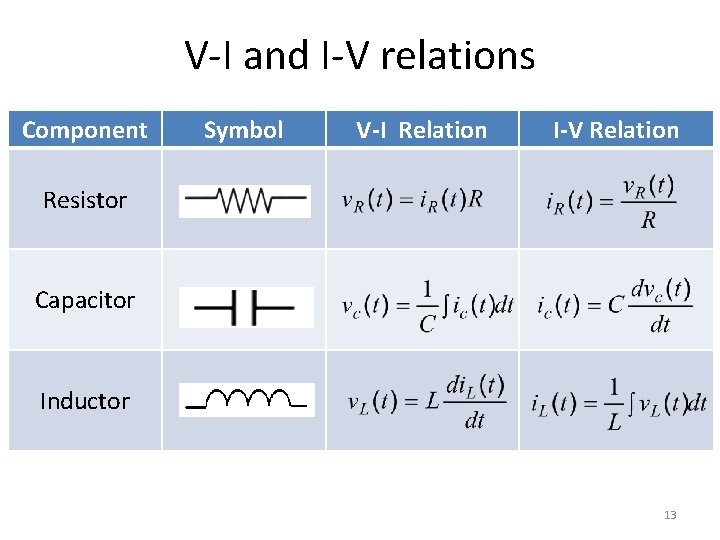
V-I and I-V relations Component Symbol V-I Relation I-V Relation Resistor Capacitor Inductor 13

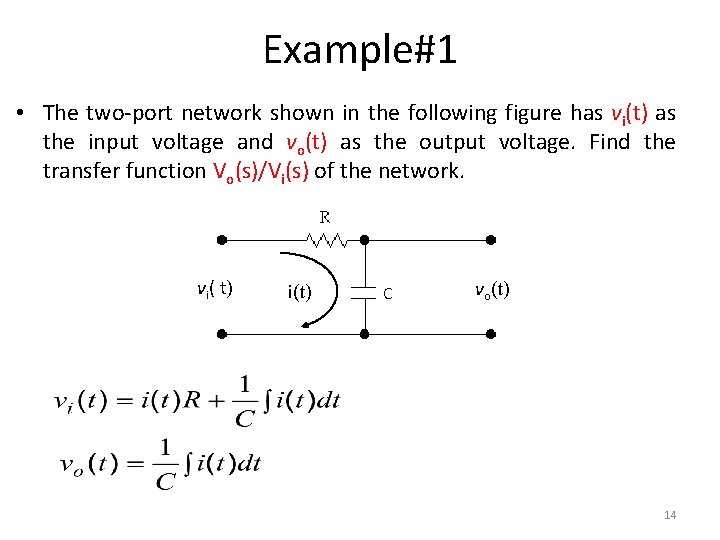
Example#1 • The two-port network shown in the following figure has vi(t) as the input voltage and vo(t) as the output voltage. Find the transfer function Vo(s)/Vi(s) of the network. vi( t) i(t) C vo(t) 14

Example#1 • Taking Laplace transform of both equations, considering initial conditions to zero. • Re-arrange both equations as: 15

Example#1 • Substitute I(s) in equation on left 16

Example#1 • The system has one pole at 17

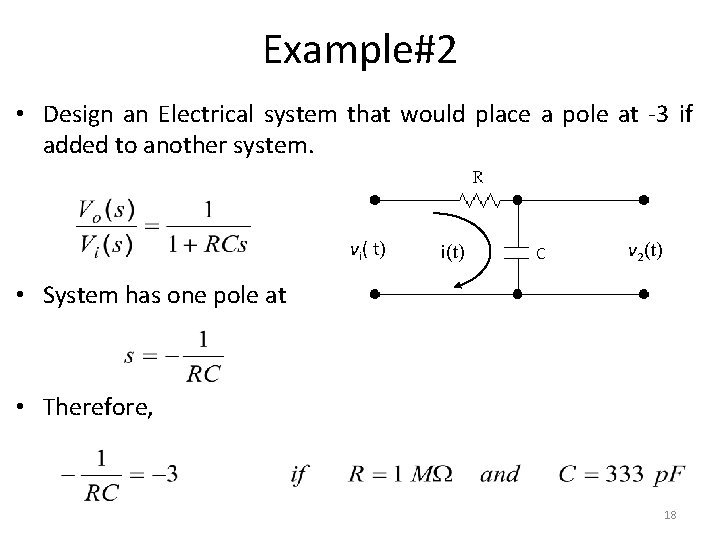
Example#2 • Design an Electrical system that would place a pole at -3 if added to another system. vi( t) i(t) C v 2(t) • System has one pole at • Therefore, 18

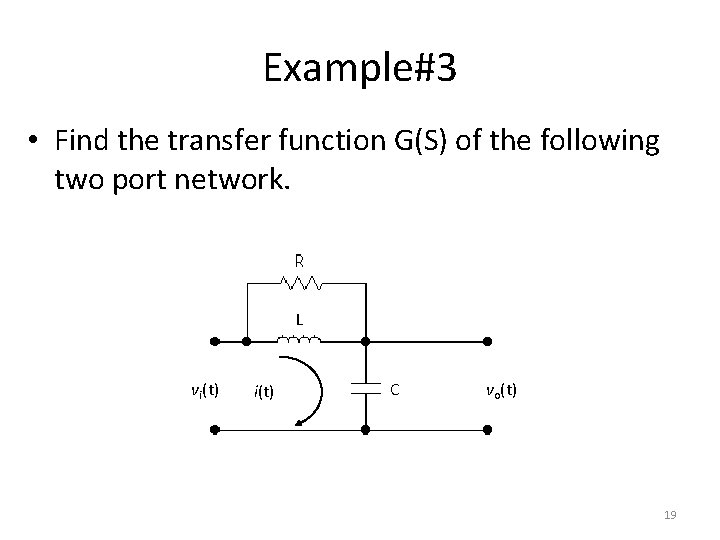
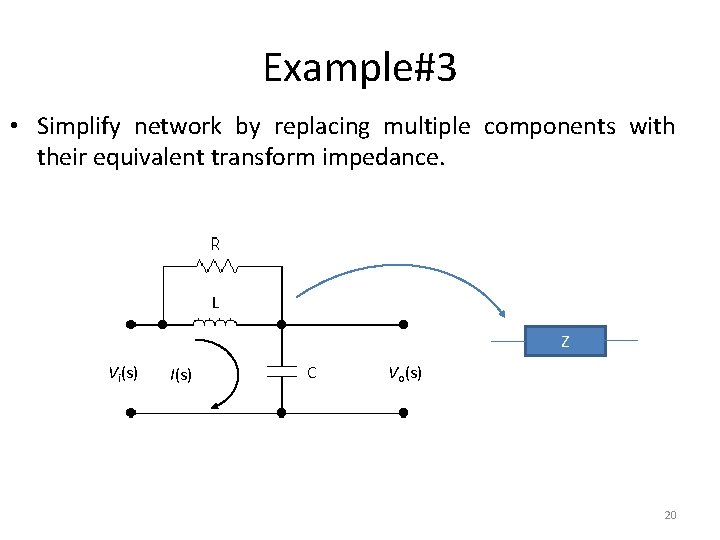
Example#3 • Find the transfer function G(S) of the following two port network. L vi(t) C vo(t) 19

Example#3 • Simplify network by replacing multiple components with their equivalent transform impedance. L Z Vi(s) I(s) C Vo(s) 20

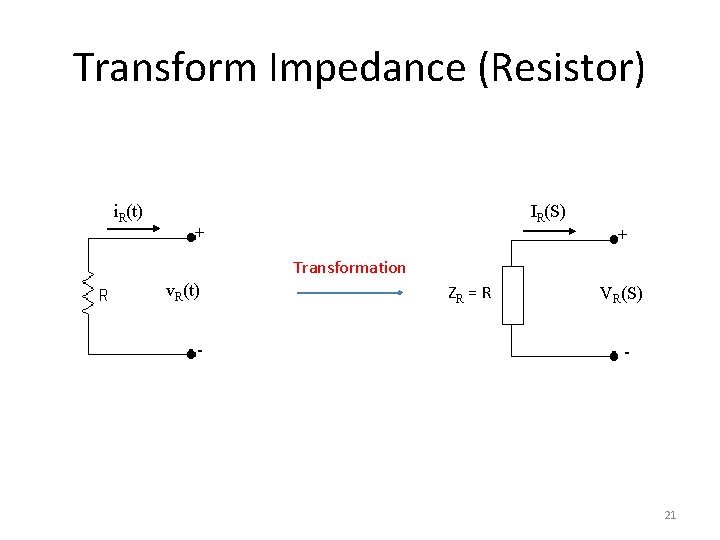
Transform Impedance (Resistor) i. R(t) IR(S) + + Transformation v. R(t) - ZR = R VR(S) - 21

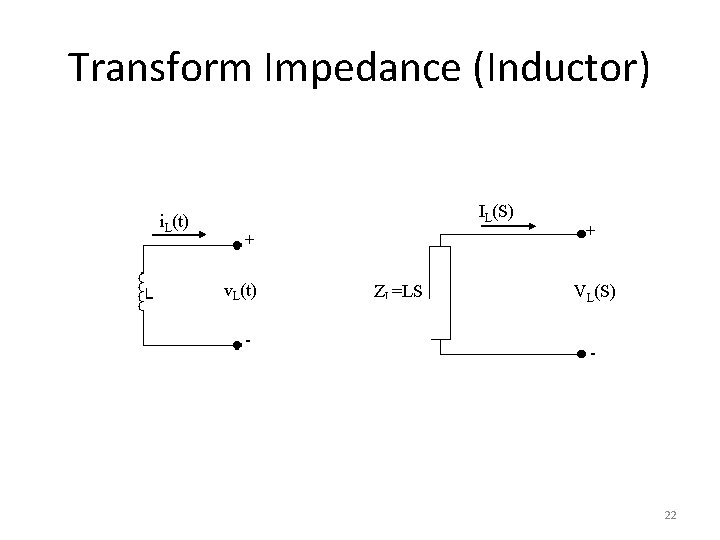
Transform Impedance (Inductor) i. L(t) IL(S) + v. L(t) - ZL=LS + VL(S) Li. L(0) - 22

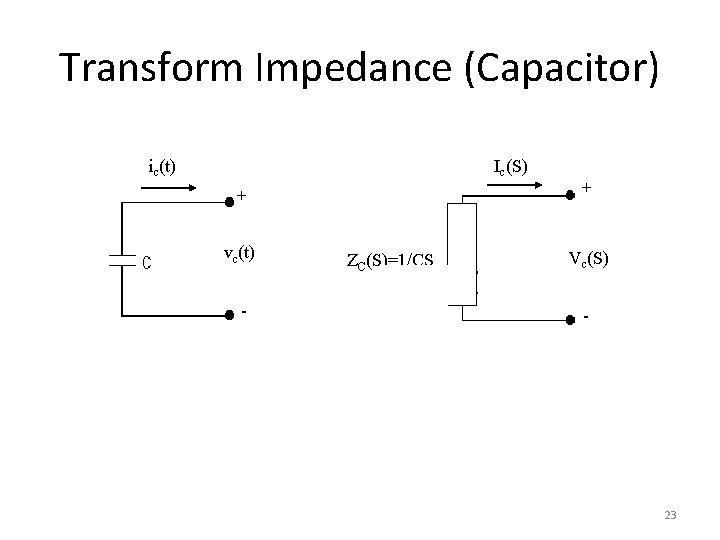
Transform Impedance (Capacitor) ic(t) Ic(S) + vc(t) - ZC(S)=1/CS + Vc(S) - 23

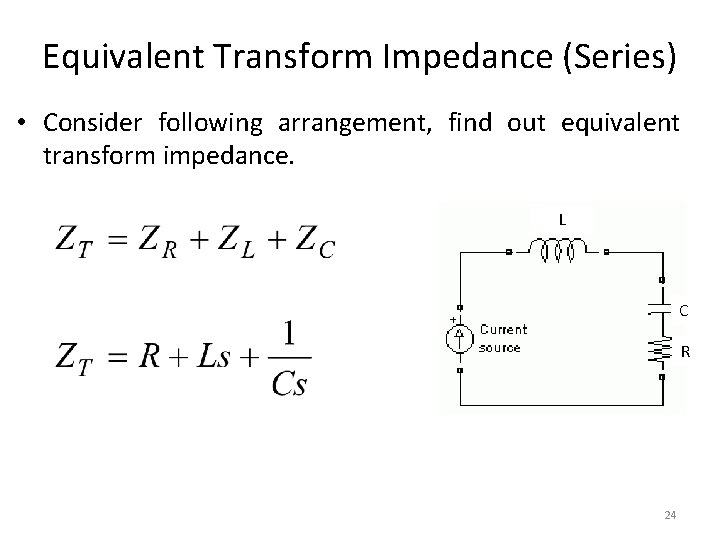
Equivalent Transform Impedance (Series) • Consider following arrangement, find out equivalent transform impedance. L C R 24

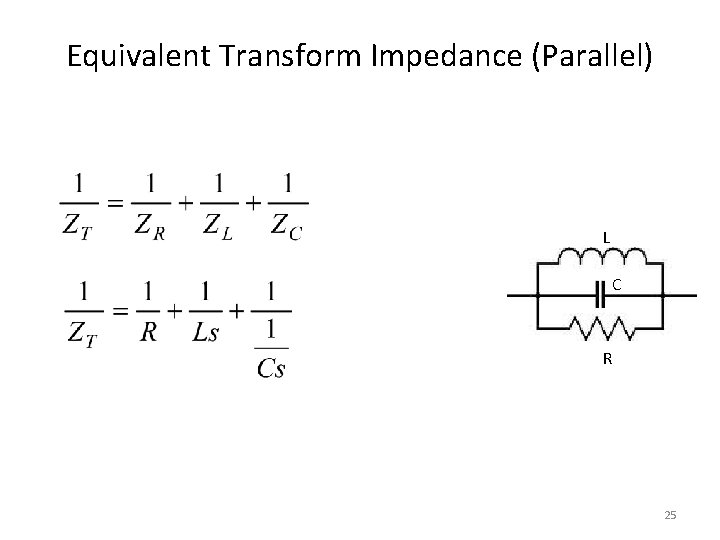
Equivalent Transform Impedance (Parallel) L C R 25

Equivalent Transform Impedance • Find out equivalent transform impedance of following arrangement. L 2 R 1 R 2 26

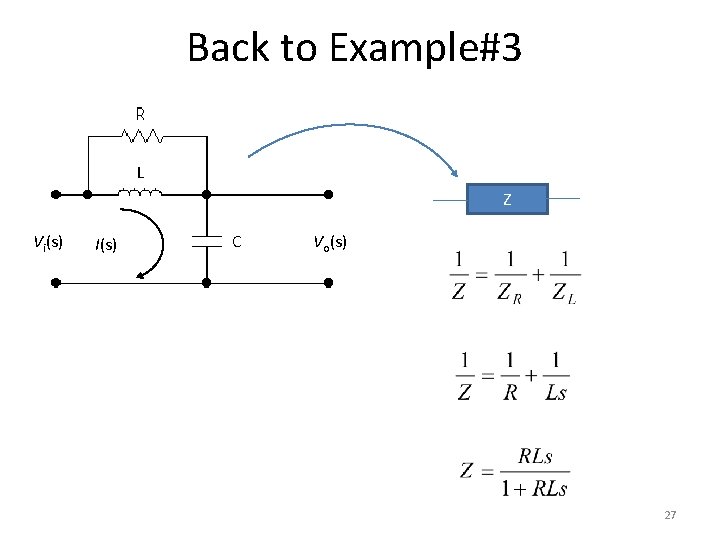
Back to Example#3 L Z Vi(s) I(s) C Vo(s) 27

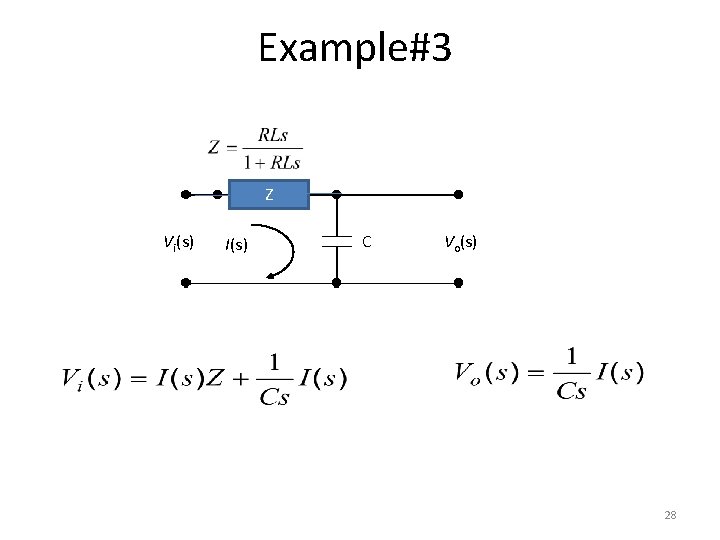
Example#3 L Z Vi(s) I(s) C Vo(s) 28

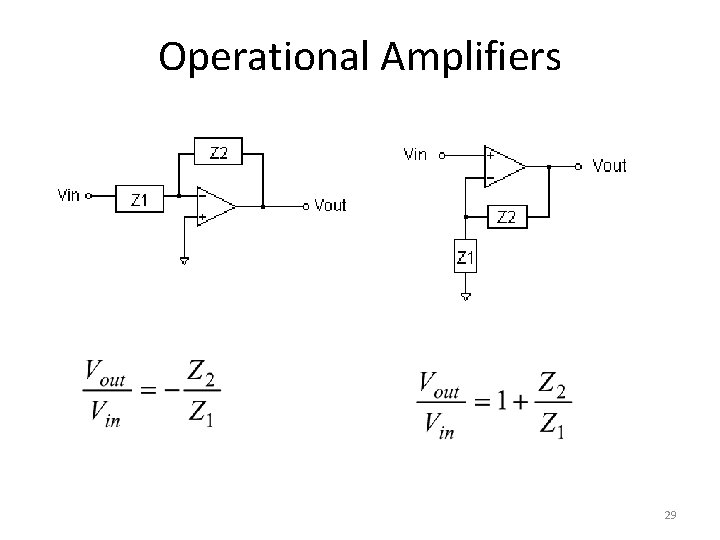
Operational Amplifiers 29

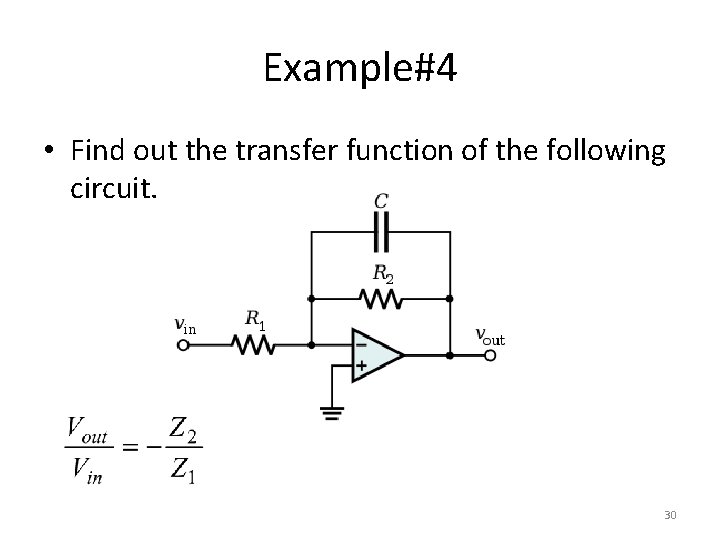
Example#4 • Find out the transfer function of the following circuit. 30

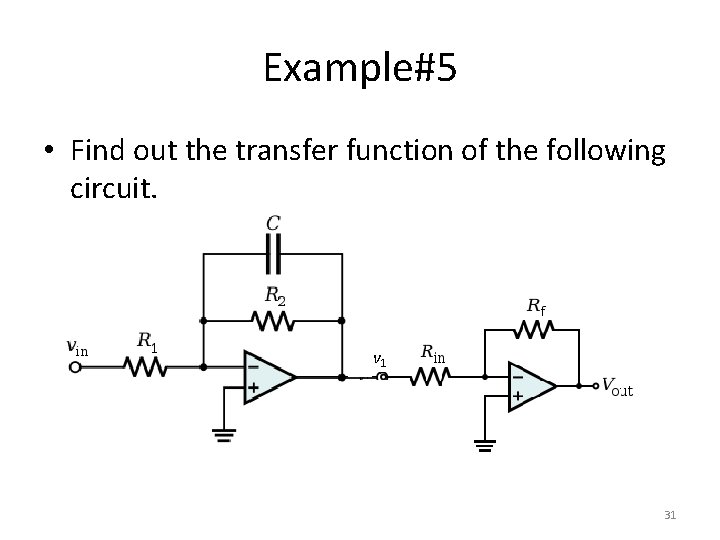
Example#5 • Find out the transfer function of the following circuit. v 1 31

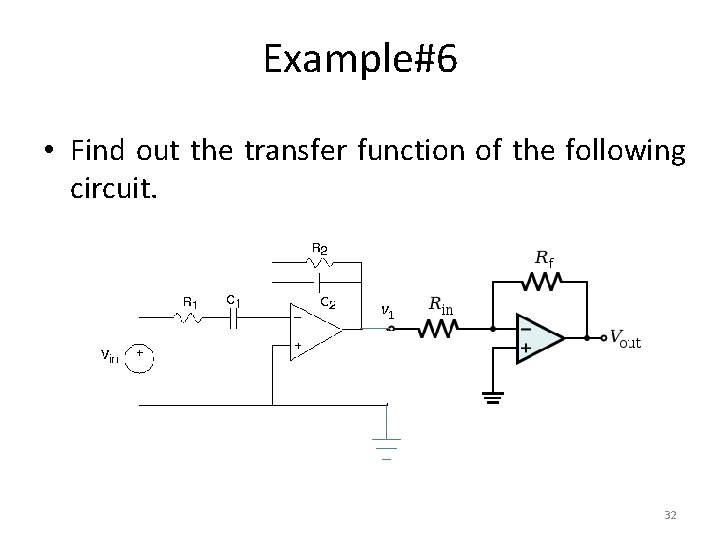
Example#6 • Find out the transfer function of the following circuit. v 1 32

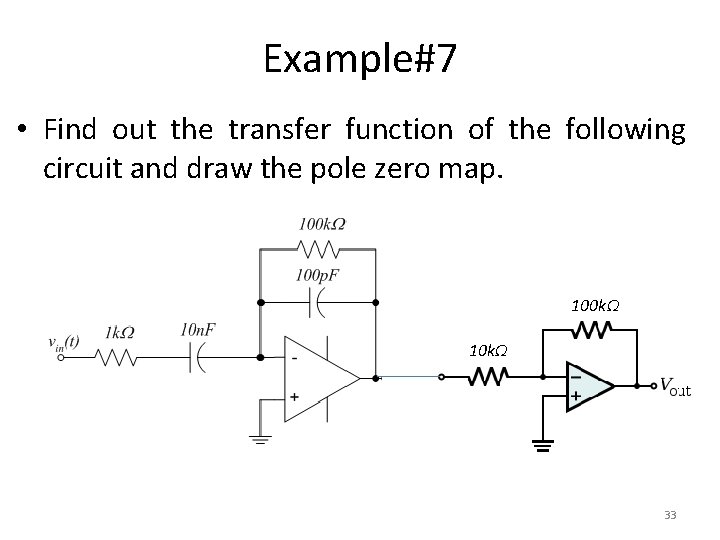
Example#7 • Find out the transfer function of the following circuit and draw the pole zero map. 100 kΩ 10 kΩ 33

To download this lecture visit http: //imtiazhussainkalwar. weebly. com/ END OF LECTURE-3 34