Control of MultipleInput Multiple Chapter 18 Output MIMO

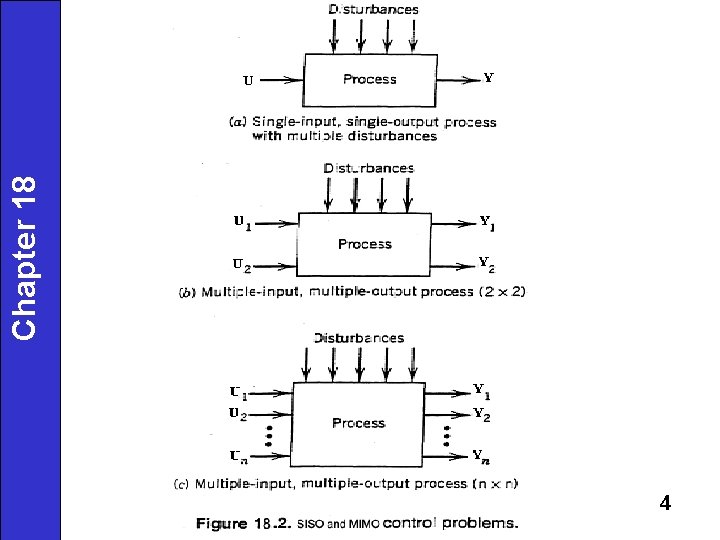
Control of Multiple-Input, Multiple- Chapter 18 Output (MIMO) Processes 18. 1 Process Interactions and Control Loop Interactions 18. 2 Pairing of Controlled and Manipulated Variables 18. 3 Singular Value Analysis 18. 4 Tuning of Multiloop PID Control Systems 18. 5 Decoupling and Multivariable Control Strategies 18. 6 Strategies for Reducing Control Loop Interactions 1

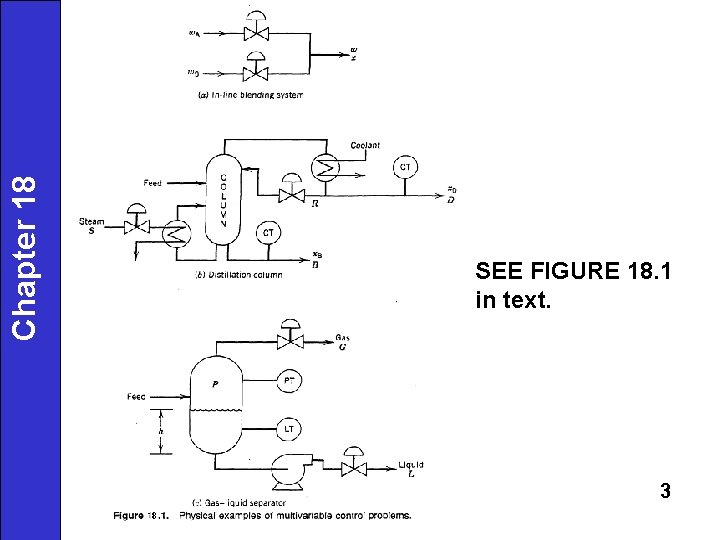
Control of Multivariable Processes Chapter 18 · In practical control problems there typically are a number of process variables which must be controlled and a number which can be manipulated. Example: product quality and throughput must usually be controlled. • Several simple physical examples are shown in Fig. 18. 1. Note the "process interactions" between controlled and manipulated variables. 2

Chapter 18 SEE FIGURE 18. 1 in text. 3

4 Chapter 18

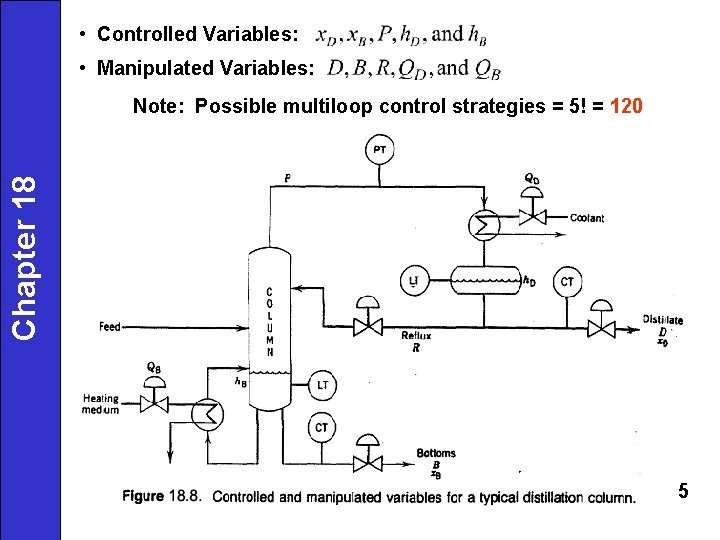
• Controlled Variables: • Manipulated Variables: Chapter 18 Note: Possible multiloop control strategies = 5! = 120 5

· In this chapter we will be concerned with characterizing process interactions and selecting an appropriate multiloop control configuration. Chapter 18 · If process interactions are significant, even the best multiloop control system may not provide satisfactory control. · In these situations there are incentives for considering multivariable control strategies. Definitions: • Multiloop control: Each manipulated variable depends on only a single controlled variable, i. e. , a set of conventional feedback controllers. • Multivariable Control: Each manipulated variable can depend on two or more of the controlled variables. Examples: decoupling control, model predictive control 6

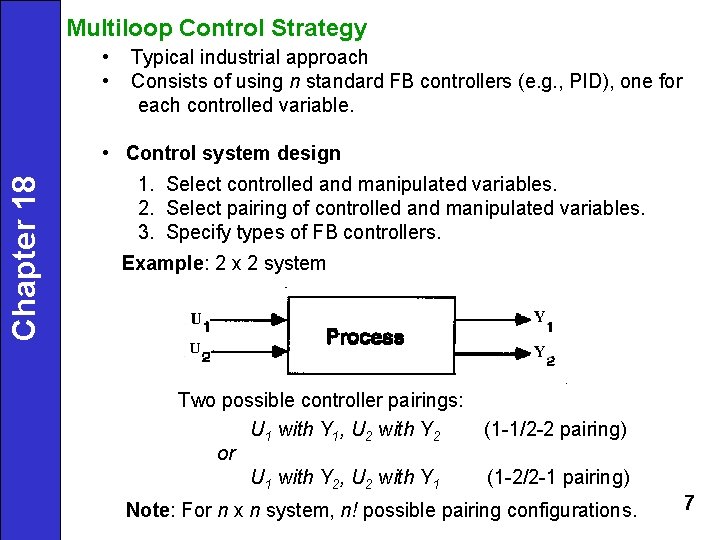
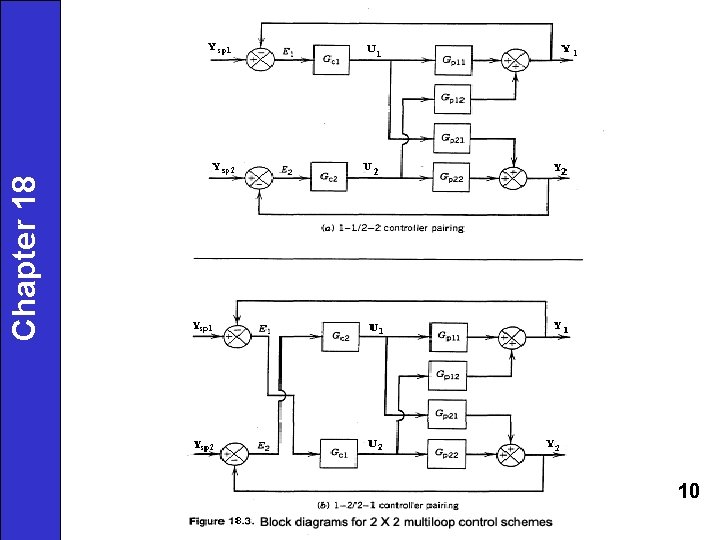
Multiloop Control Strategy • • Typical industrial approach Consists of using n standard FB controllers (e. g. , PID), one for each controlled variable. Chapter 18 • Control system design 1. Select controlled and manipulated variables. 2. Select pairing of controlled and manipulated variables. 3. Specify types of FB controllers. Example: 2 x 2 system Two possible controller pairings: U 1 with Y 1, U 2 with Y 2 or U 1 with Y 2, U 2 with Y 1 (1 -1/2 -2 pairing) (1 -2/2 -1 pairing) Note: For n x n system, n! possible pairing configurations. 7

Transfer Function Model (2 x 2 system) Chapter 18 Two controlled variables and two manipulated variables (4 transfer functions required) Thus, the input-output relations for the process can be written as: 8

Chapter 18 Or in vector-matrix notation as, where Y(s) and U(s) are vectors, And Gp(s) is the transfer function matrix for the process 9

10 Chapter 18

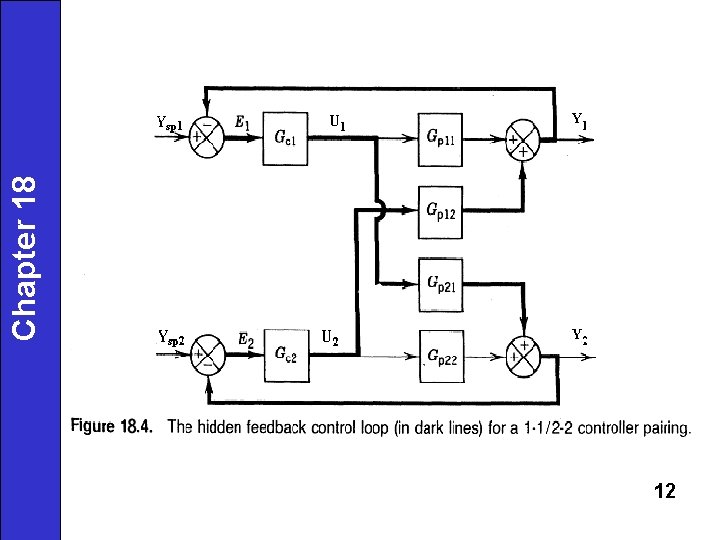
Control-loop Interactions Chapter 18 • Process interactions may induce undesirable interactions between two or more control loops. Example: 2 x 2 system Control loop interactions are due to the presence of a third feedback loop. • Problems arising from control loop interactions i. Closed-loop system may become destabilized. ii. Controller tuning becomes more difficult. 11

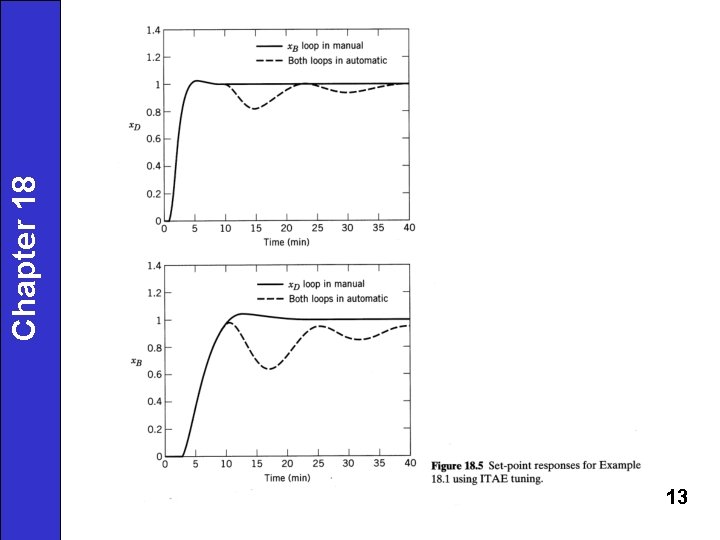
12 Chapter 18

13 Chapter 18

Chapter 18 Block Diagram Analysis For the multiloop control configuration, the transfer function between a controlled and a manipulated variable depends on whether the other feedback control loops are open or closed. Example: 2 x 2 system, 1 -1/2 -2 pairing From block diagram algebra we can show (second loop open) (18 -7) (second loop closed) (18 -11) Note that the last expression contains GC 2. 14

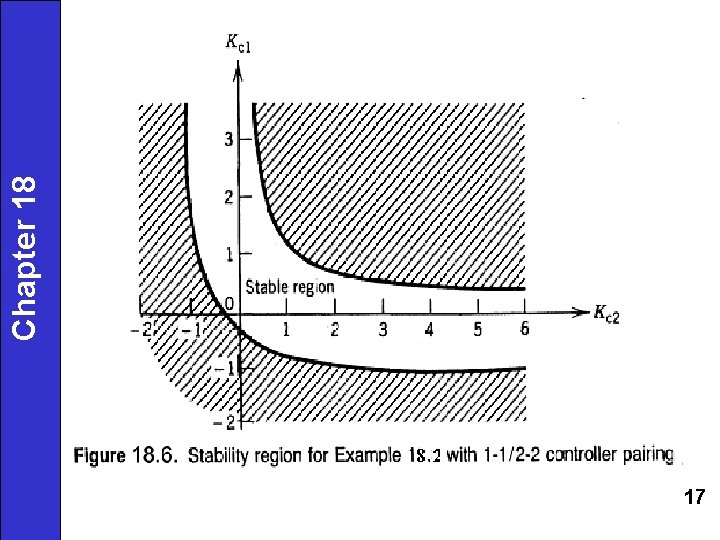
15 Chapter 18

16 Chapter 18

17 Chapter 18

18 Chapter 18

Relative Gain Array Chapter 18 • Provides two types of useful information: 1. Measure of process interactions 2. Recommendation about best pairing of controlled and manipulated variables. • Requires knowledge of steady-state gains but not process dynamics. 19

Example of RGA Analysis: 2 x 2 system Chapter 18 • Steady-state process model, The RGA, L, is defined as: where the relative gain, ij, relates the ith controlled variable and the jth manipulated variable 20

Scaling Properties: Chapter 18 i. ij is dimensionless ii. For a 2 x 2 system, (18 -34) Recommended Controller Pairing It corresponds to the ij which have the largest positive values that are closest to one. 21

Chapter 18 In general: 1. Pairings which correspond to negative pairings should not be selected. 2. Otherwise, choose the pairing which has ij closest to one. Examples: Process Gain Matrix, K : Relative Gain Array, L : 22

Chapter 18 For 2 x 2 systems: Example 1: Recommended pairing is Y 1 and U 1, Y 2 and U 2. Example 2: Recommended pairing is Y 1 with U 1 and Y 2 with U 2. 23

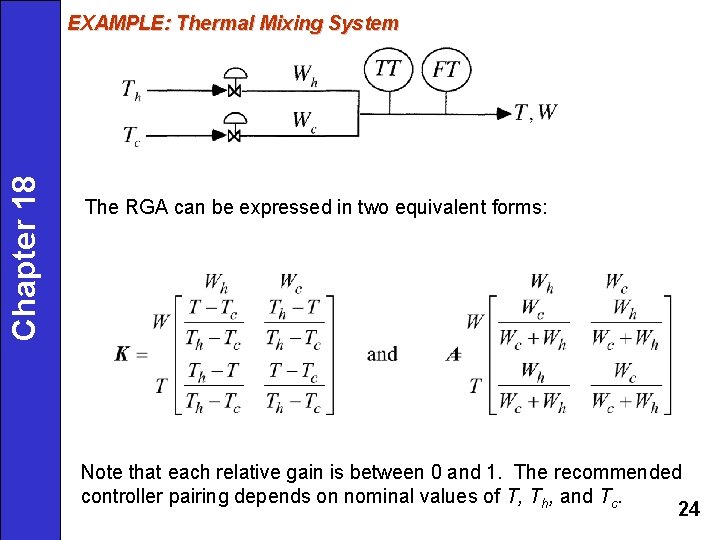
Chapter 18 EXAMPLE: Thermal Mixing System The RGA can be expressed in two equivalent forms: Note that each relative gain is between 0 and 1. The recommended controller pairing depends on nominal values of T, Th, and Tc. 24

RGA for Higher-Order Systems Chapter 18 For and n x n system, Each ij can be calculated from the relation, where Kij is the (i, j) -element of the steady-state gain K matrix, Hij is the (i, j) -element of the Note : .

Example: Hydrocracker Chapter 18 The RGA for a hydrocracker has been reported as, Recommended controller pairing? 26

Chapter 18 Singular Value Analysis • Any real m x n matrix can be factored as, T K=WSV • Matrix S is a diagonal matrix of singular values: S = diag (s 1, s 2, …, sr) • The singular values are the positive square roots of the T T eigenvalues of K K ( r = the rank of K K). • The columns of matrices W and V are orthonormal. Thus, T T WW = I and VV = I • Can calculate S, W, and V using MATLAB command, svd. • Condition number (CN) is defined to be the ratio of the largest to the smallest singular value, • A large value of CN indicates that K is ill-conditioned. 27

Chapter 18 Condition Number • CN is a measure of sensitivity of the matrix properties to changes in individual elements. • Consider the RGA for a 2 x 2 process, • If K 12 changes from 0 to 0. 1, then K becomes a singular matrix, which corresponds to a process that is difficult to control. • RGA and SVA used together can indicate whether a process is easy (or difficult) to control. • K is poorly conditioned when CN is a large number (e. g. , > 10). Thus small changes in the model for this process can make it very difficult to control. 28

Selection of Inputs and Outputs Chapter 18 • • • Arrange the singular values in order of largest to smallest and look for any σi/σi-1 > 10; then one or more inputs (or outputs) can be deleted. Delete one row and one column of K at a time and evaluate the properties of the reduced gain matrix. Example: 29

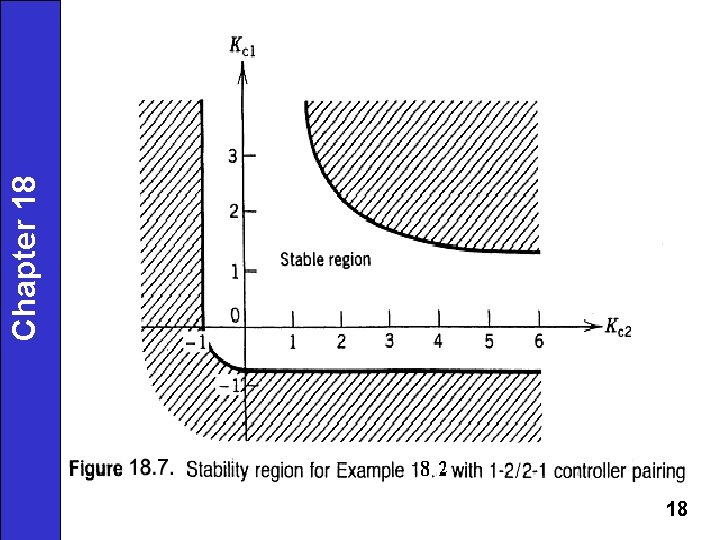
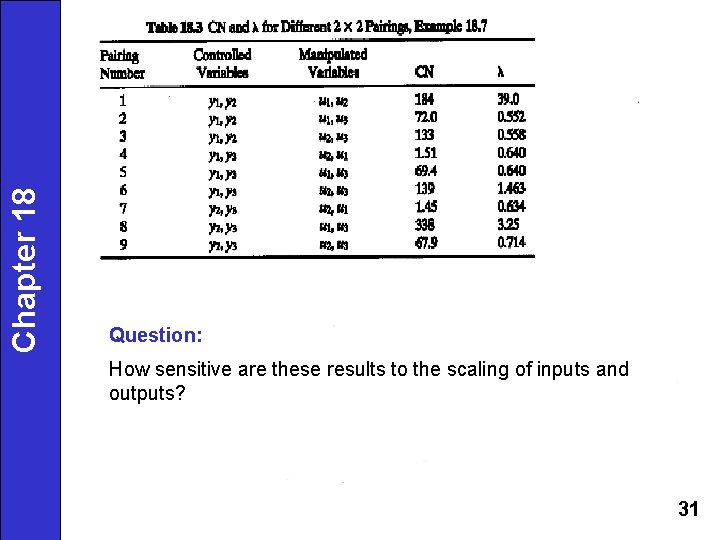
Chapter 18 18 • CN = 166. 5 (σ1/σ3) The RGA is: Preliminary pairing: y 1 -u 2, y 2 -u 3, y 3 -u 1. CN suggests only two output variables can be controlled. Eliminate one input and one output (3 x 3→ 2 x 2). 30

Chapter 18 Question: How sensitive are these results to the scaling of inputs and outputs? 31

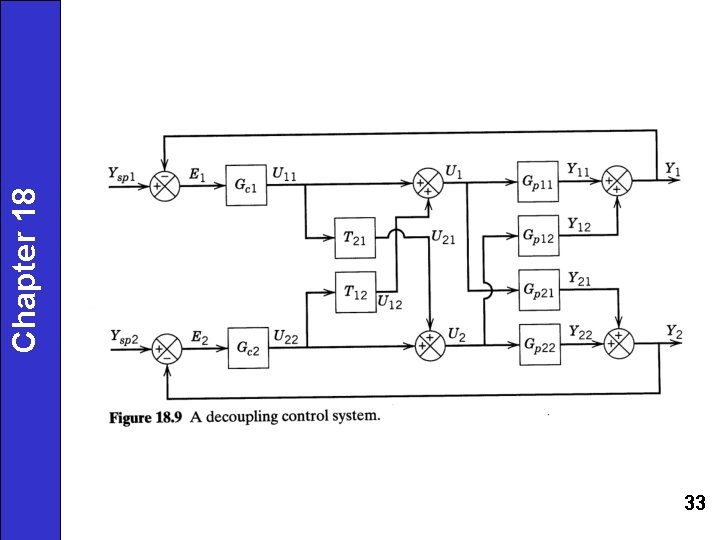
Chapter 18 Alternative Strategies for Dealing with Undesirable Control Loop Interactions 1. "Detune" one or more FB controllers. 2. Select different manipulated or controlled variables. e. g. , nonlinear functions of original variables 3. Use a decoupling control scheme. 4. Use some other type of multivariable control scheme. Decoupling Control Systems · Basic Idea: Use additional controllers to compensate for process interactions and thus reduce control loop interactions · Ideally, decoupling control allows setpoint changes to affect only the desired controlled variables. · Typically, decoupling controllers are designed using a simple process model (e. g. , a steady-state model or transfer function model) 32

33 Chapter 18

Decoupler Design Equations Chapter 18 We want cross-controller, T 12, to cancel the effect of U 2 on Y 1. Thus, we would like, Because U 22 0 in general, then Similarly, we want T 12 to cancel the effect of U 1 on Y 2. Thus, we require that, Compare with the design equations for feedforward control based on block diagram analysis 34

Variations on a Theme 1. Partial Decoupling: Chapter 18 Use only one “cross-controller. ” 2. Static Decoupling: Design to eliminate SS interactions Ideal decouplers are merely gains: 3. Nonlinear Decoupling Appropriate for nonlinear processes. 35

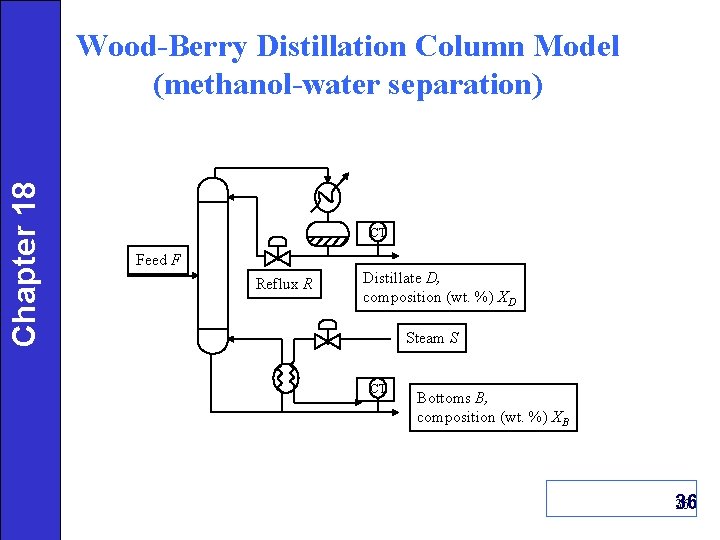
Chapter 18 Wood-Berry Distillation Column Model (methanol-water separation) CT Feed F Reflux R Distillate D, composition (wt. %) XD Steam S CT Bottoms B, composition (wt. %) XB 36 36 36

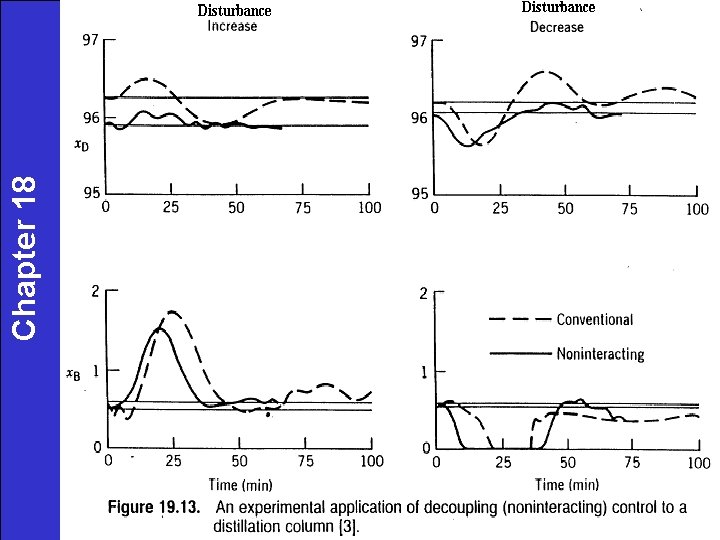
Chapter 18 Wood-Berry Distillation Column Model 3737

Chapter 18