Control 3 Keypoints PID control Steadystate error and

Control 3 Keypoints: • PID control • Steady-state error and the integral method • Overshoot and ringing in system with time delay • Overshoot and ringing in second order systems • The derivative method

PID control • • P = Proportional error I = Integral D = Derivative A standard and very useful method for augmenting simple feedback control – E. g. used in wheel position/speed control in the Khepera

Proportional error control Desired output Control Law Actual output Motor command Measurement Robot in environment Disturbances • Same as servo, i. e. using a control signal proportional to the difference between the actual (measured) output and the desired (target) output. • I. e. want to make large change when error is large, small change if error is small

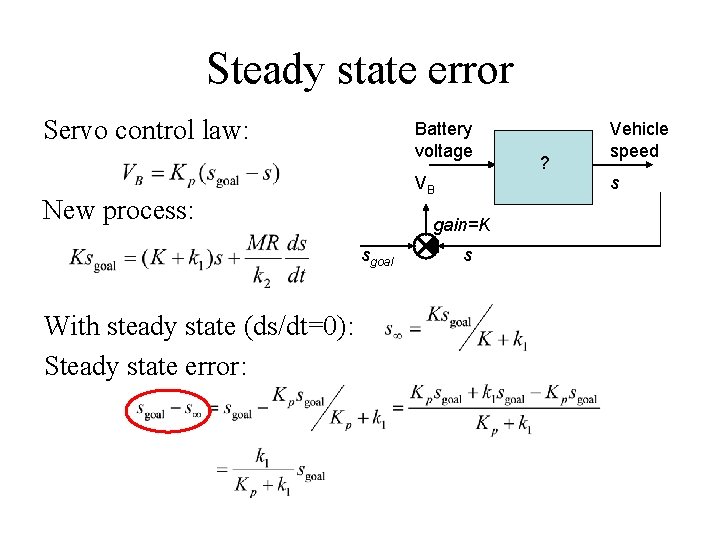
Steady state error Servo control law: Battery voltage VB New process: With steady state (ds/dt=0): Steady state error: s gain=K sgoal ? Vehicle speed s

Steady state error Battery voltage VB ? Vehicle speed s gain=K sgoal s k 1 is determined by the motor physics: e= k 1 s Can choose Kp: to reach target want But we can’t put an infinite voltage into our motor!

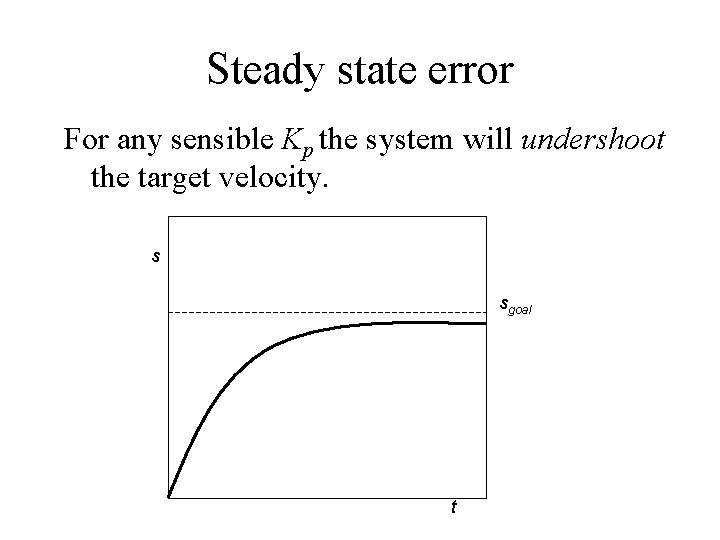
Steady state error For any sensible Kp the system will undershoot the target velocity. s sgoal t

Proportional Integral (PI) Control If we could estimate this error we could add it to the control signal: The best way to estimate it is to integrate the error over time: Obtain new control law: Basically, this sums some fraction of the error until the error is reduced to zero. With careful choice of Kp and Ki this can eliminate the steady state error.

Feedback with time delays Desired output Control Law Actual output Motor command Measurement Robot in environment Disturbances • Imagine trying to move a robot to some zero position with the simple control law: – If xt < -δ move forward at 1 cm/second, – If xt > δ move backward at 1 cm/second, – If -δ < xt < δ stop • What happens if there is a 1 second delay in feedback?

Feedback with time delays • In general, a time-lag in a feedback loop will result in overshoot and oscillation. • Depending on the dynamics, the oscillation could fade out, continue or increase. • Sometimes we want oscillation, e. g. CPG

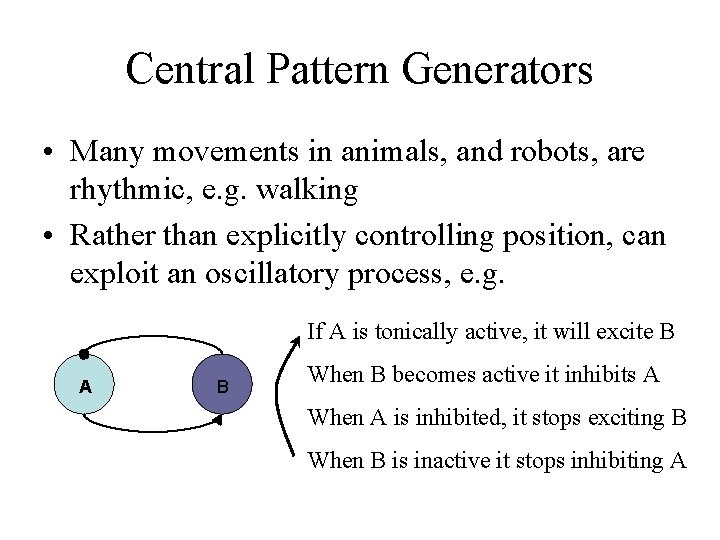
Central Pattern Generators • Many movements in animals, and robots, are rhythmic, e. g. walking • Rather than explicitly controlling position, can exploit an oscillatory process, e. g. If A is tonically active, it will excite B A B When B becomes active it inhibits A When A is inhibited, it stops exciting B When B is inactive it stops inhibiting A

Feedback with time delays • In general, a time-lag in a feedback loop will result in overshoot and oscillation. • Depending on the dynamics, the oscillation could fade out, continue or increase. • Sometimes we want oscillation, e. g. CPG • Note that integration introduces a time delay. • Time delays are equivalent to energy storage e. g. inertia will cause similar effects.

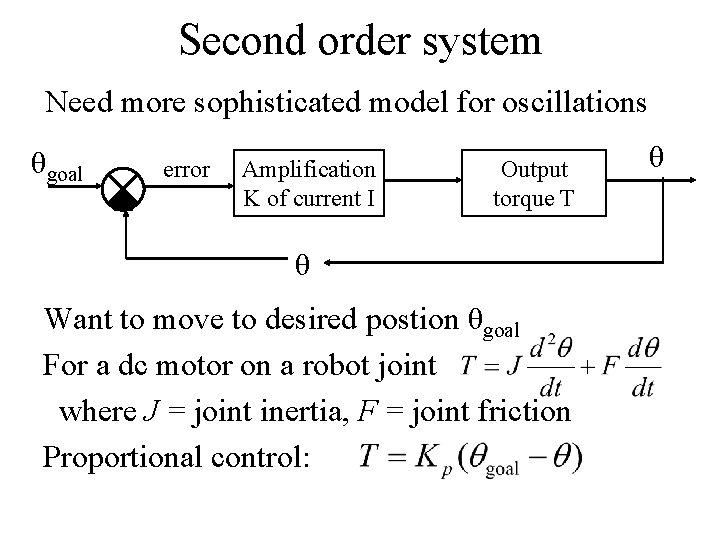
Second order system Need more sophisticated model for oscillations θgoal error Amplification K of current I Output torque T θ Want to move to desired postion θgoal For a dc motor on a robot joint where J = joint inertia, F = joint friction Proportional control: θ

Second order system solution For simplicity let Then the system process is • The solution to this equation has the form where [May be complex] The system behaviour depends on J, F, Kp as follows:

Over and Under Damping The system returns to the goal with over-damping The system returns to the goal with under-damped, sinusoidal behaviour

Steady state error – Load Droop • If the system has to hold a load against gravity, it requires a constant torque • But PE controller cannot do this without error, as torque is proportional to error (so, needs some error) • If we knew the load L could use • But in practice this is not often possible

Proportional integral (PI) control • As before, we integrate the error over time, i. e. • Effectively this gradually increases L until it produces enough torque to compensate for the load • PI copes with Load Droop

Proportional derivative (PD) control • Commonly, inertia is large and friction small • Consequently the system overshoots, reverses the error and control signal, overshoots again… • To actively brake the motion, we want to apply negative torque when error is small and velocity high • Make Artificial friction:

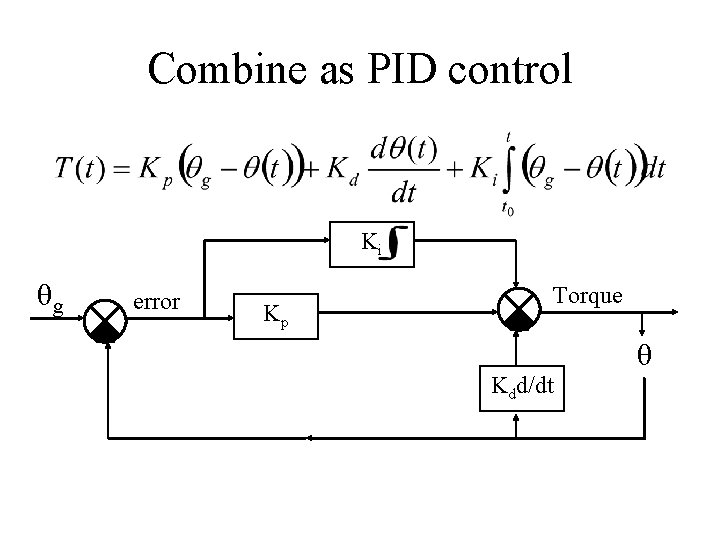
Combine as PID control Ki θg error Kp Torque Kdd/dt θ

PID control demo Rearranging becomes (almost) solveable as:

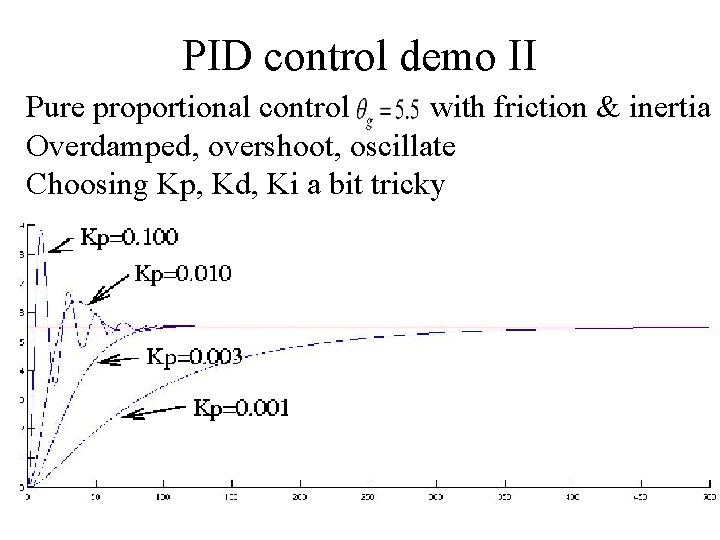
PID control demo II Pure proportional control with friction & inertia Overdamped, overshoot, oscillate Choosing Kp, Kd, Ki a bit tricky

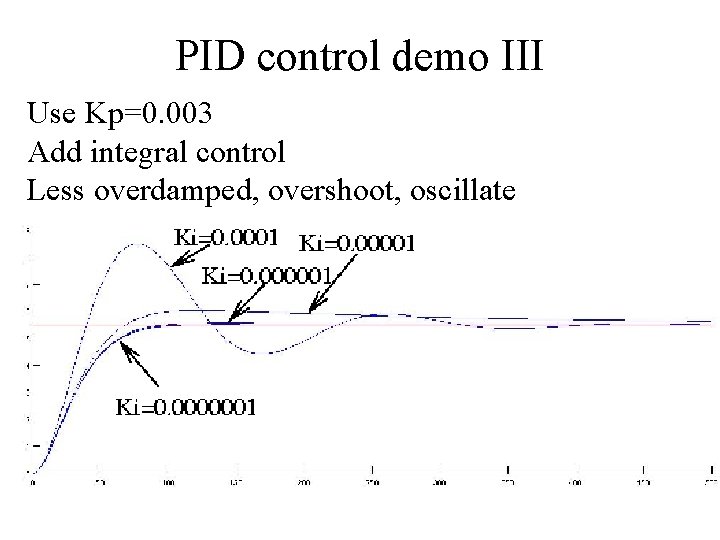
PID control demo III Use Kp=0. 003 Add integral control Less overdamped, overshoot, oscillate

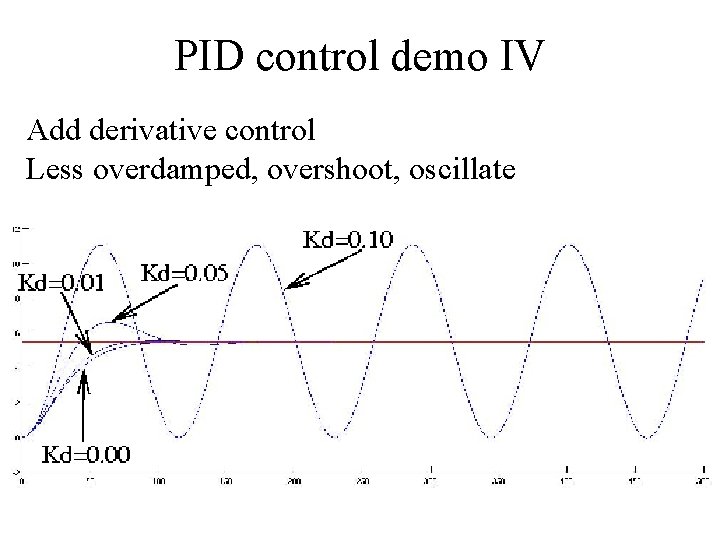
PID control demo IV Add derivative control Less overdamped, overshoot, oscillate

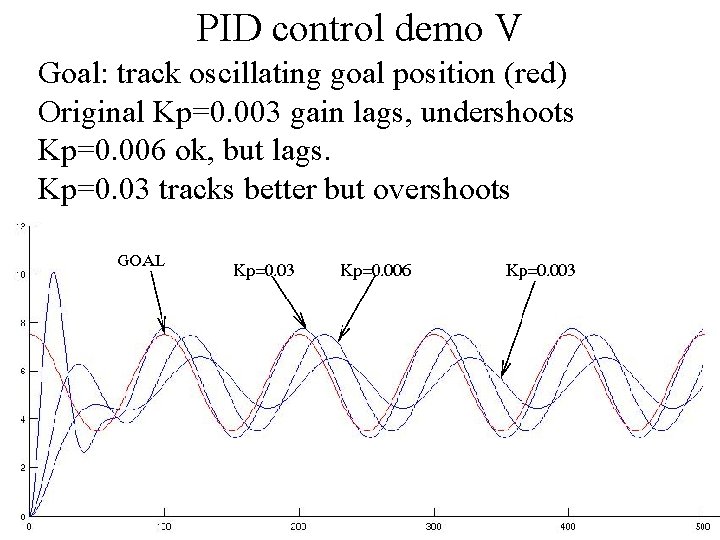
PID control demo V Goal: track oscillating goal position (red) Original Kp=0. 003 gain lags, undershoots Kp=0. 006 ok, but lags. Kp=0. 03 tracks better but overshoots

Further reading: Most standard control textbooks discuss PID control. For the research on robot juggling see: Rizzi, A. A. & Koditschek, D. E. (1994) Further progress in robot juggling: Solvable mirror laws. IEEE International Conference on Robotics and Automation 2935 -2940 S. Schaal and C. G. Atkeson. Open Loop Stable Control Strategies for Robot Juggling. In Proc. IEEE Conf. Robotics and Automation, pages 913 -- 918, Atlanta, Georgia, 1993. CPGs are used in many more recent examples of walking robots.