Contrasts Statistical Inference Christophe Phillips SPM Course London

![Contrasts [1 0 0 0 0] [0 1 -1 0 0 0] Contrasts [1 0 0 0 0] [0 1 -1 0 0 0]](https://slidetodoc.com/presentation_image/a294565473f846d71ad17b36a4109696/image-5.jpg)





![Scaling issue Subject 1 [1 1 1 1 ] / 4 q The T-statistic Scaling issue Subject 1 [1 1 1 1 ] / 4 q The T-statistic](https://slidetodoc.com/presentation_image/a294565473f846d71ad17b36a4109696/image-12.jpg)






- Slides: 28

Contrasts & Statistical Inference Christophe Phillips SPM Course London, May 2018

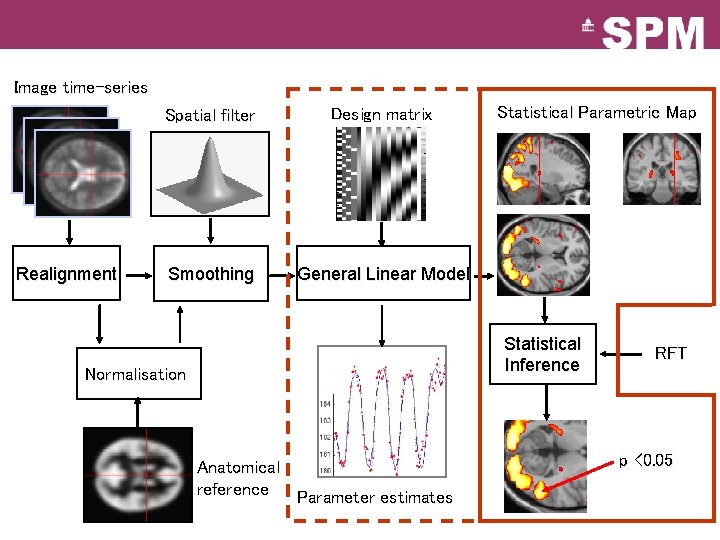
Image time-series Realignment Spatial filter Design matrix Smoothing General Linear Model Statistical Parametric Map Statistical Inference Normalisation Anatomical reference Parameter estimates RFT p <0. 05

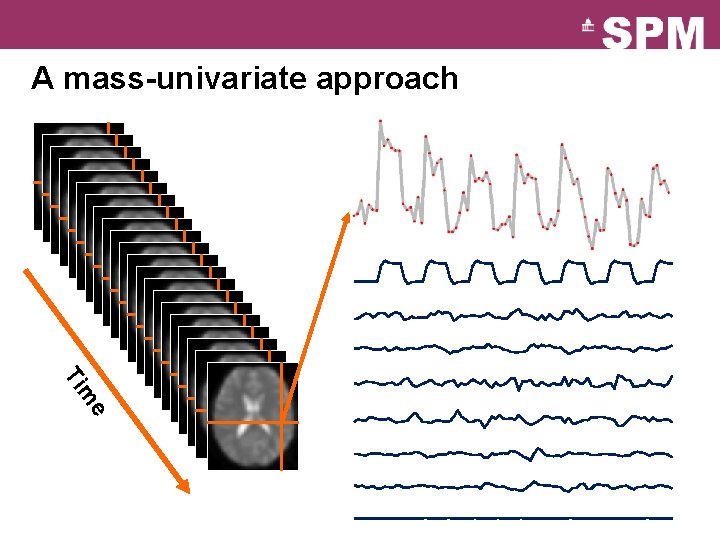
A mass-univariate approach e m Ti

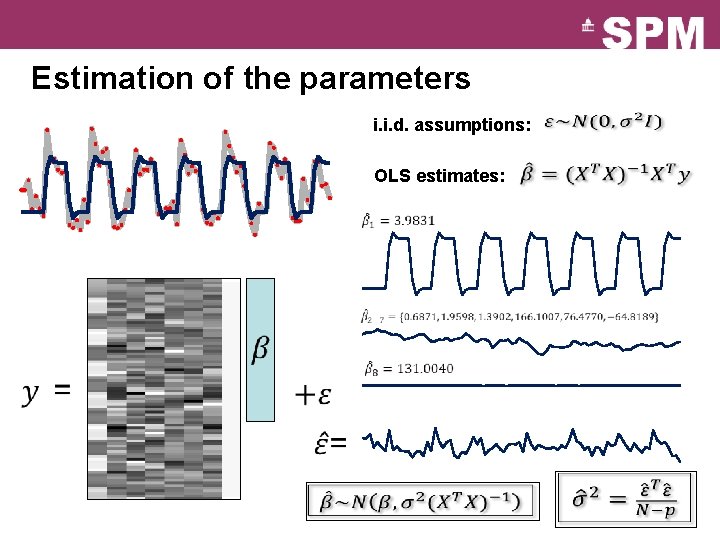
Estimation of the parameters i. i. d. assumptions: OLS estimates:
![Contrasts 1 0 0 0 0 0 1 1 0 0 0 Contrasts [1 0 0 0 0] [0 1 -1 0 0 0]](https://slidetodoc.com/presentation_image/a294565473f846d71ad17b36a4109696/image-5.jpg)
Contrasts [1 0 0 0 0] [0 1 -1 0 0 0]

Hypothesis Testing To test a hypothesis, we construct “test statistics”. q Null Hypothesis H 0 Typically what we want to disprove (no effect). The Alternative Hypothesis HA expresses outcome of interest. q Test Statistic T The test statistic summarises evidence about H 0. Typically, test statistic is small in magnitude when the hypothesis H 0 is true and large when false. We need to know the distribution of T under the null hypothesis. Null Distribution of T

Hypothesis Testing u q Significance level α: Acceptable false positive rate α. threshold uα Threshold uα controls the false positive rate Null Distribution of T q Conclusion about the hypothesis: We reject the null hypothesis in favour of the alternative hypothesis if t > uα q p-value: A p-value summarises evidence against H 0. This is the chance of observing value more extreme than t under the null hypothesis. t p-value Null Distribution of T

T-test - one dimensional contrasts – SPM{t} c. T =10000000 b 1 b 2 b 3 b 4 b 5. . . Question: box-car amplitude > 0 ? = b 1 = c. Tb> 0 ? H 0: c. Tb=0 Null hypothesis: contrast of estimated parameters Test statistic: T= variance estimate

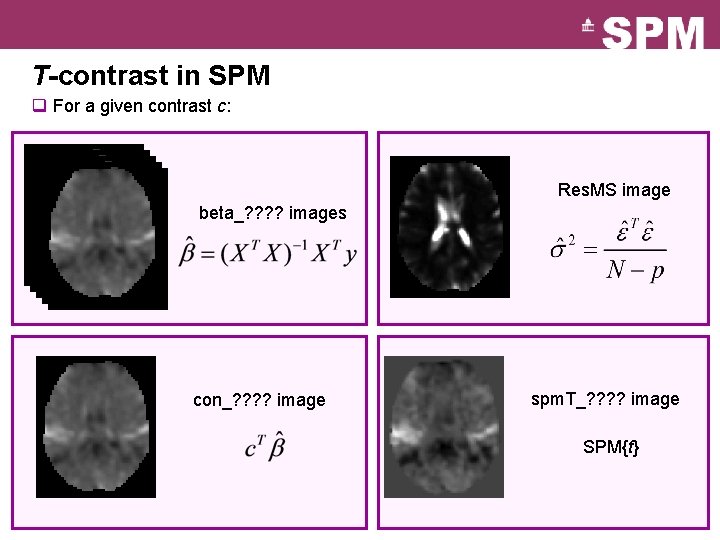
T-contrast in SPM q For a given contrast c: Res. MS image beta_? ? images con_? ? image spm. T_? ? image SPM{t}

T-test: a simple example q Passive word listening versus rest c. T = [ 1 0 0 0 0] 1 Q: activation during listening ? Null hypothesis: SPMresults: Height threshold T = 3. 2057 {p<0. 001} voxel-level T 13. 94 12. 04 11. 82 13. 72 12. 29 9. 89 7. 39 6. 84 6. 36 6. 19 5. 96 5. 84 5. 44 5. 32 ( Zº) Inf Inf Inf 7. 83 6. 36 5. 99 5. 65 5. 53 5. 36 5. 27 4. 97 4. 87 puncorrected 0. 000 0. 000 mm mm mm -63 -48 -66 57 63 57 36 51 -63 -30 36 -45 48 36 -27 15 -33 12 -21 6 -21 12 -3 -39 6 -30 -15 0 48 -54 -3 -33 -18 -27 9 42 9 27 24 -27 42

T-test: summary q T-test is a signal-to-noise measure (ratio of estimate to standard deviation of estimate). q Alternative hypothesis: H 0: vs HA: q T-contrasts are simple combinations of the betas; the Tstatistic does not depend on the scaling of the regressors or the scaling of the contrast.
![Scaling issue Subject 1 1 1 1 1 4 q The Tstatistic Scaling issue Subject 1 [1 1 1 1 ] / 4 q The T-statistic](https://slidetodoc.com/presentation_image/a294565473f846d71ad17b36a4109696/image-12.jpg)
Scaling issue Subject 1 [1 1 1 1 ] / 4 q The T-statistic does not depend on the scaling of the regressors. q The T-statistic does not depend on the scaling of the contrast. Subject 5 [1 1 1 ] / 3 q Contrast depends on scaling. Ø Be careful of the interpretation of the contrasts themselves (eg, for a second level analysis): sum ≠ average

F-test - the extra-sum-of-squares principle q Model comparison: Null Hypothesis H 0: True model is X 0 (reduced model) X 0 X 1 Test statistic: ratio of explained variability and unexplained variability (error) RSS 0 Full model ? or Reduced model? 1 = rank(X) – rank(X 0) 2 = N – rank(X)

F-test - multidimensional contrasts – SPM{F} q Tests multiple linear hypotheses: H 0: True model is X 0 X 1 (b 4 -9) H 0: b 4 = b 5 =. . . = b 9 = 0 X 0 c. T = test H 0 : c. Tb = 0 ? 0001000001000001000 000000100 000000010 00001 SPM{F 6, 322} Full model? Reduced model?

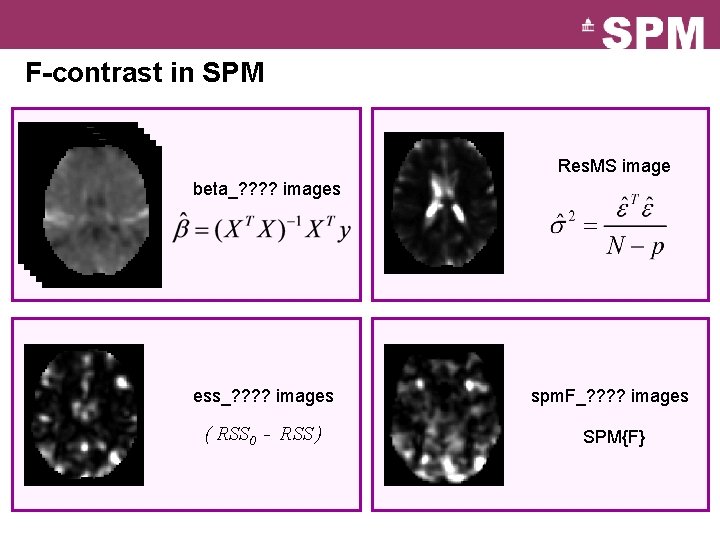
F-contrast in SPM Res. MS image beta_? ? images ess_? ? images spm. F_? ? images ( RSS 0 - RSS ) SPM{F}

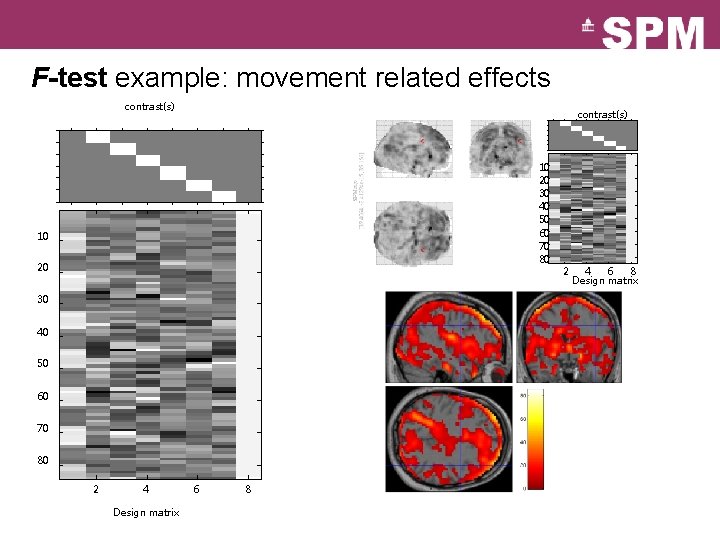
F-test example: movement related effects contrast(s) 10 20 30 40 50 60 70 80 2 4 Design matrix 6 8 2 4 6 8 Design matrix

F-test: summary q F-tests can be viewed as testing for the additional variance explained by a larger model wrt a simpler (nested) model comparison. q F tests a weighted sum of squares of one or several combinations of the regression coefficients b. q In practice, we don’t have to explicitly separate X into [X 1 X 2] thanks to multidimensional contrasts. q Hypotheses: q In testing uni-dimensional contrast with an F-test, for example b 1 – b 2, the result will be the same as testing b 2 – b 1. It will be exactly the square of the t-test, testing for both positive and negative effects.

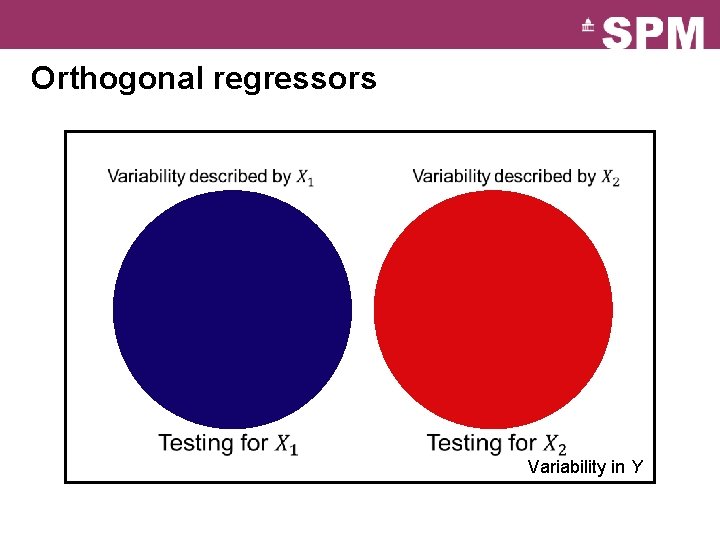
Orthogonal regressors Variability in Y

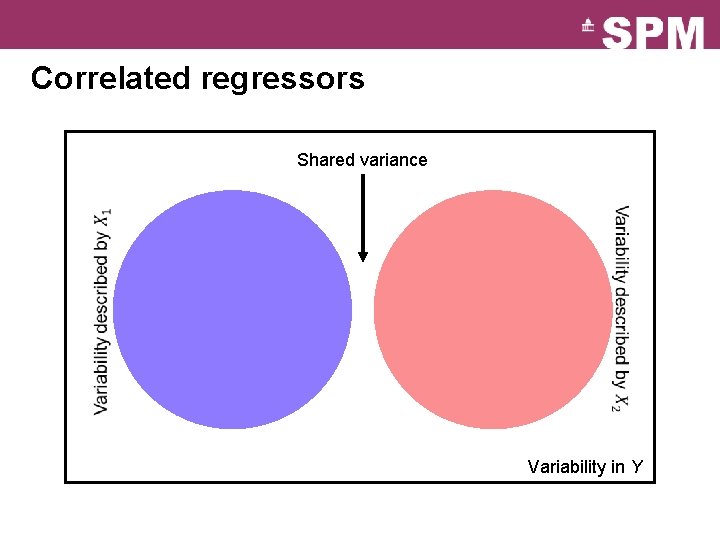
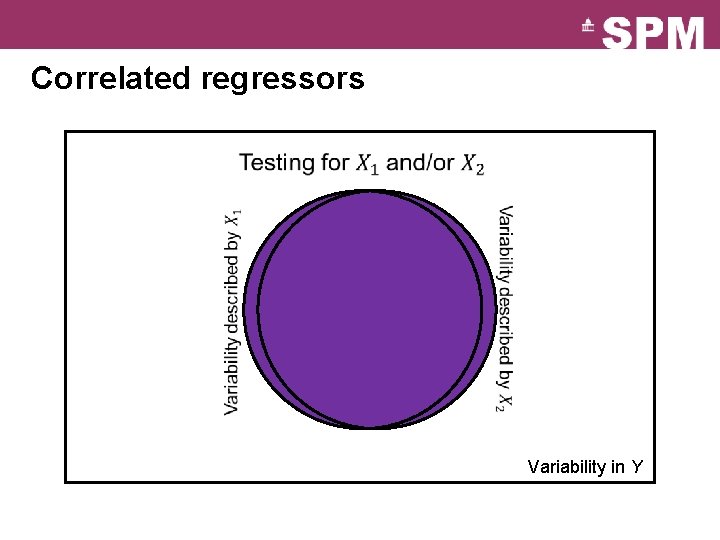
Correlated regressors Shared variance Variability in Y

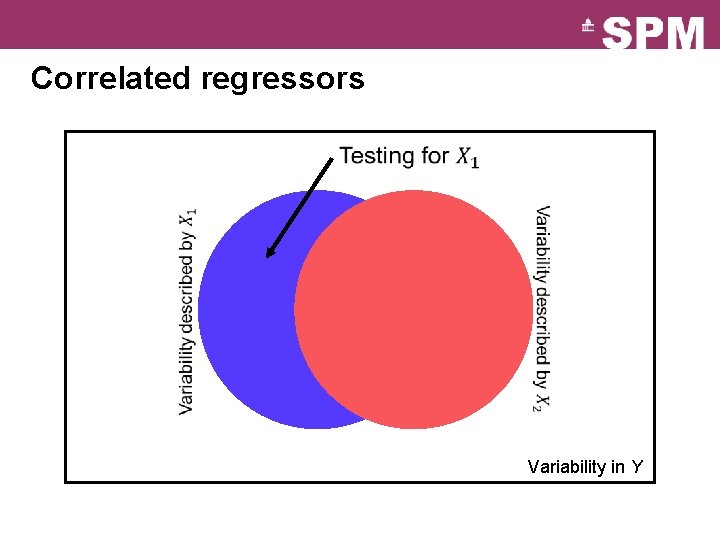
Correlated regressors Variability in Y

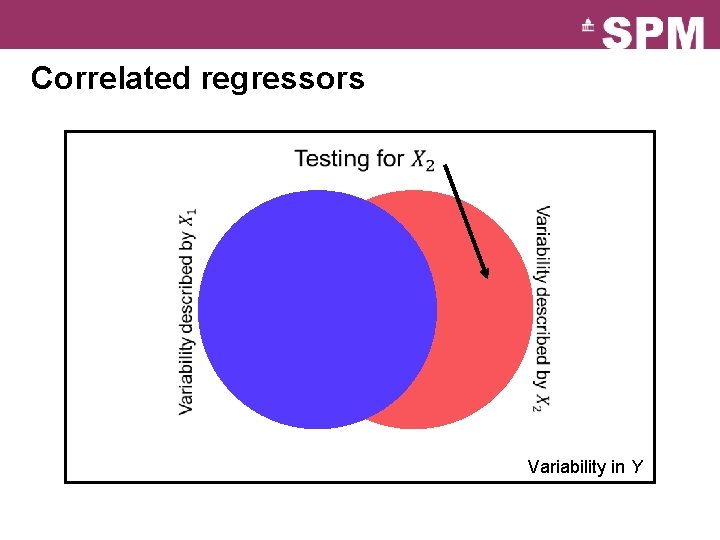
Correlated regressors Variability in Y

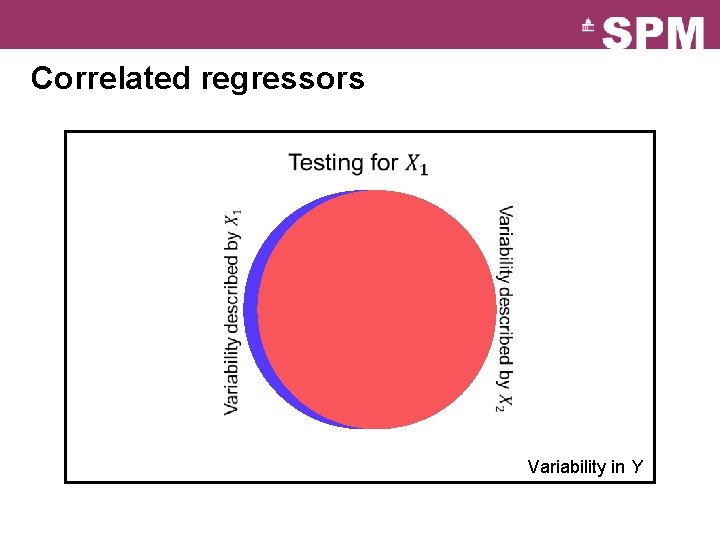
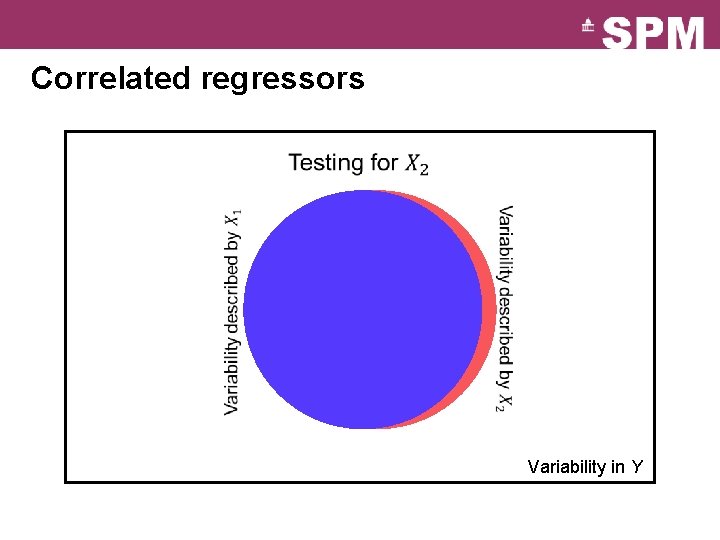
Correlated regressors Variability in Y

Correlated regressors Variability in Y

Correlated regressors Variability in Y

Correlated regressors Variability in Y

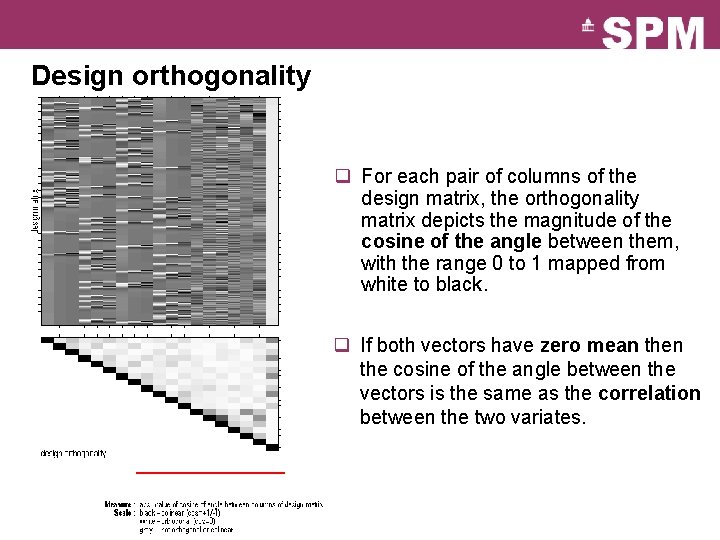
Design orthogonality q For each pair of columns of the design matrix, the orthogonality matrix depicts the magnitude of the cosine of the angle between them, with the range 0 to 1 mapped from white to black. q If both vectors have zero mean the cosine of the angle between the vectors is the same as the correlation between the two variates.

Correlated regressors: summary q We implicitly test for an additional effect only. When testing for the first regressor, we are effectively removing the part of the signal that can be accounted for by the second regressor: implicit orthogonalisation. x^2 x 2 x 1 x^ 1 x 2 x^2 = x 2 – x 1. x 2 x 1 q Orthogonalisation = decorrelation. Parameters and test on the non modified regressor change. Rarely solves the problem as it requires assumptions about which regressor to uniquely attribute the common variance. change regressors (i. e. design) instead, e. g. factorial designs. use F-tests to assess overall significance. q Original regressors may not matter: it’s the contrast you are testing which should be as decorrelated as possible from the rest of the design matrix

Bibliography: q Statistical Parametric Mapping: The Analysis of Functional Brain Images. Elsevier, 2007. q Plane Answers to Complex Questions: Theory of Linear Models. R. Christensen, Springer, 1996. q Statistical parametric maps in functional imaging: a general linear approach. K. J. Friston et al, Human Brain Mapping, 1995. q Ambiguous results in functional neuroimaging data analysis due to covariate correlation. A. Andrade et al. , Neuro. Image, 1999. q Estimating efficiency a priori: a comparison of blocked and randomized designs. A. Mechelli et al. , Neuro. Image, 2003.
 Christophe phillips
Christophe phillips Localisation
Localisation Spm london
Spm london Point estimate equation
Point estimate equation Proof of chebyshev's inequality
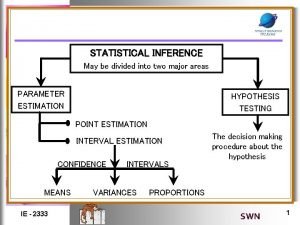
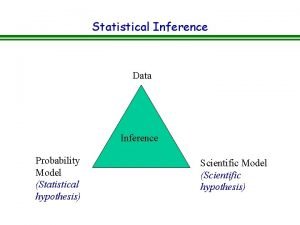
Proof of chebyshev's inequality Statistical inference is concerned with
Statistical inference is concerned with Probability and statistical inference 9th solution pdf
Probability and statistical inference 9th solution pdf Statistical inference is divided into
Statistical inference is divided into Statistical inference
Statistical inference Samantha cogging
Samantha cogging Elearning icsi
Elearning icsi Irony is a contrast between expectations and reality
Irony is a contrast between expectations and reality Planned contrasts spss
Planned contrasts spss Contrasts and contradictions signpost
Contrasts and contradictions signpost Anova planned contrasts
Anova planned contrasts Contrast and contradiction meaning
Contrast and contradiction meaning North carolina land of contrasts
North carolina land of contrasts Nonfiction signposts contrasts and contradictions
Nonfiction signposts contrasts and contradictions Chapter 5 a land of contrasts
Chapter 5 a land of contrasts Christophe delamare
Christophe delamare Christophe closset
Christophe closset Christophe muys
Christophe muys Christophe colomb
Christophe colomb Jean-christophe mercier
Jean-christophe mercier Christophe hery
Christophe hery Christophe damian
Christophe damian Diplopie monoculaire
Diplopie monoculaire Christophe douaud
Christophe douaud Christophe venet
Christophe venet