Contractibility of a persistence map preimage introduction to

Contractibility of a persistence map preimage (introduction to) Jacek Cyranka* & Konstantin Mischaikow** ATDD 2018 Montana State University *University California, San Diego, CSE Department **HAPPY BIRTHDAY ATDD’ 18, Contractibility of a persistence map preimage 1

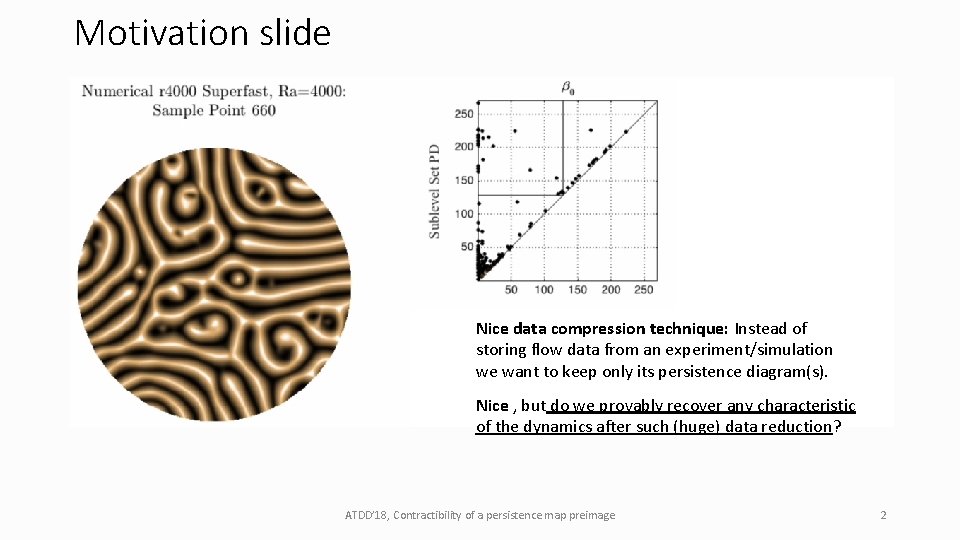
Motivation slide Nice data compression technique: Instead of storing flow data from an experiment/simulation we want to keep only its persistence diagram(s). Nice , but do we provably recover any characteristic of the dynamics after such (huge) data reduction? ATDD’ 18, Contractibility of a persistence map preimage 2

The setting of one dimensional simplicial complex Our approach: To study the topology of the preimage of the persistence map to allow for applying existing tools from algebraic topology like the Lefshetz fixed point theorem. ATDD’ 18, Contractibility of a persistence map preimage 3

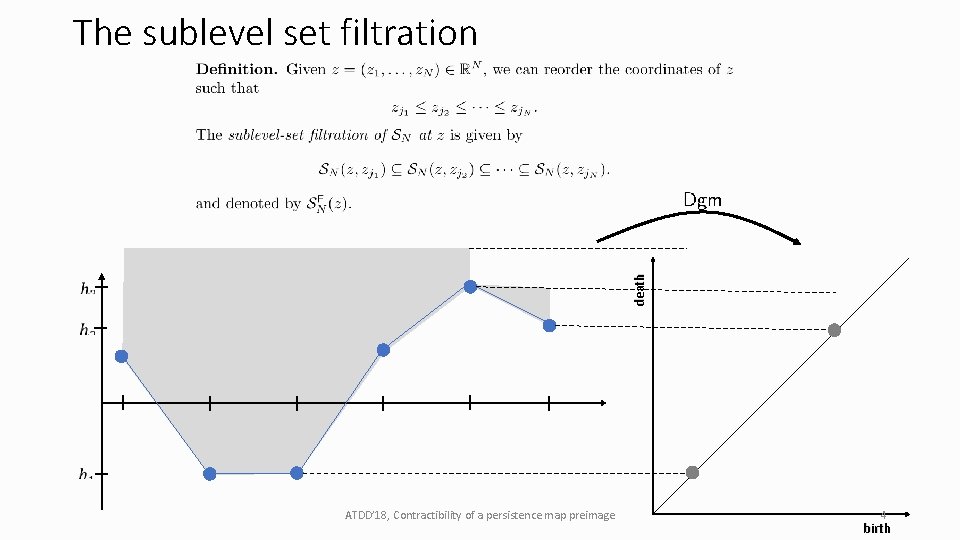
death The sublevel set filtration ATDD’ 18, Contractibility of a persistence map preimage 4 birth

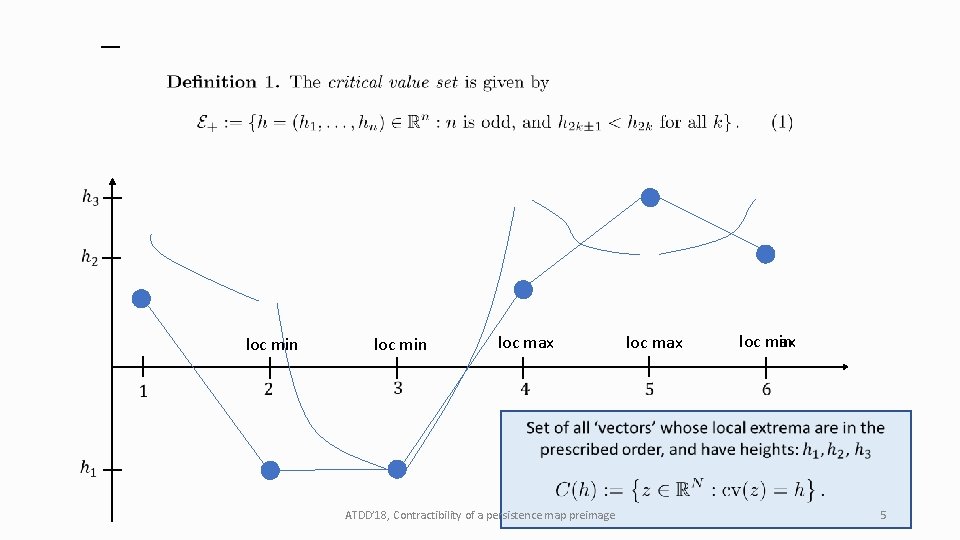
loc min loc max loc min ATDD’ 18, Contractibility of a persistence map preimage 5

Preimage of the persistence map J. Curry, The Fiber of the Persistence Map, ar. Xiv: 1706. 06059. ATDD’ 18, Contractibility of a persistence map preimage 6

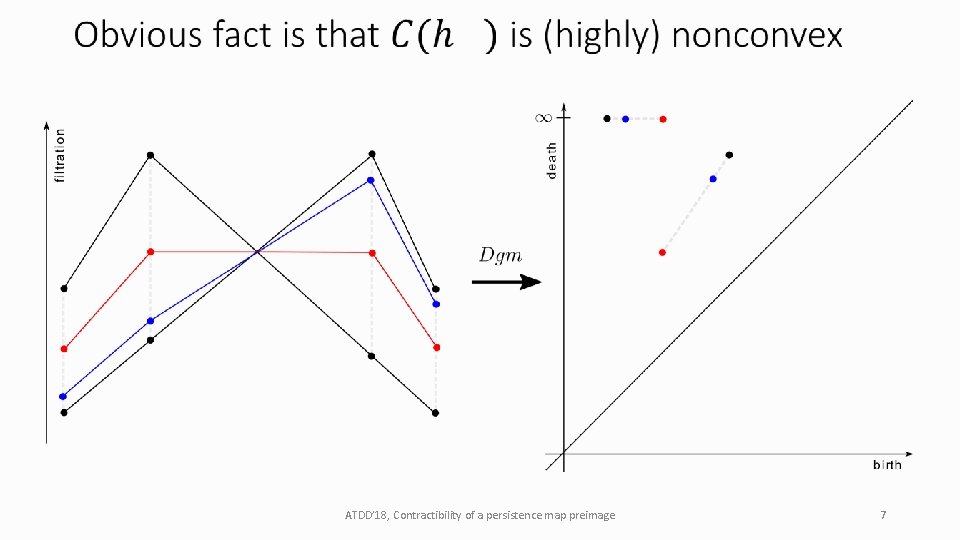
ATDD’ 18, Contractibility of a persistence map preimage 7

ATDD’ 18, Contractibility of a persistence map preimage 9

A case study of applying the Nerve theorem P. Alexandroff. Uber den allgemeinen dimensionsbegriff und seine beziehungen zur elementaren geometrischen anschauung. Mathematische Annalen, 98(1): 617– 635, 1928. K. Borsuk. On the imbedding of systems of compacta in simplicial complexes. Fund. Math. , 35: 217– 234, 1948. ATDD’ 18, Contractibility of a persistence map preimage 10

ATDD’ 18, Contractibility of a persistence map preimage 11

ATDD’ 18, Contractibility of a persistence map preimage 12

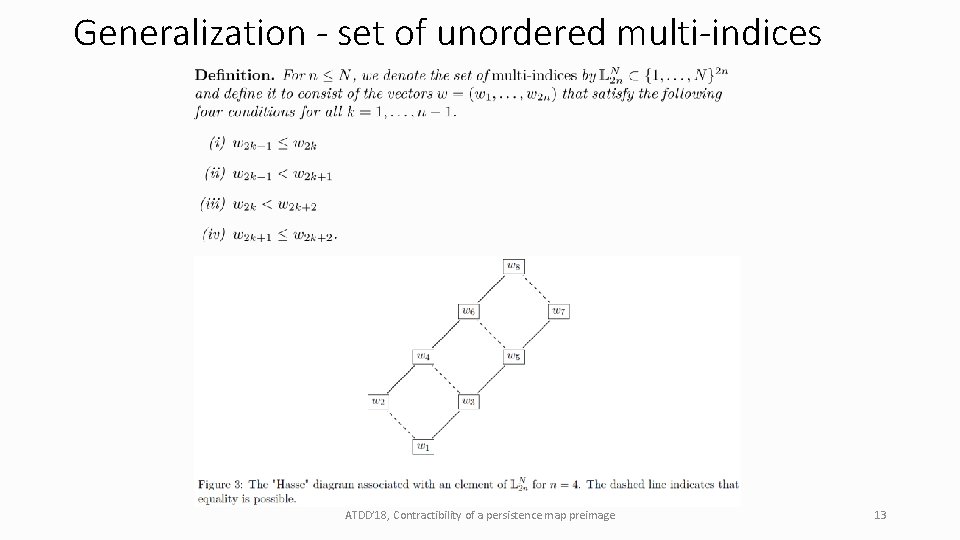
Generalization - set of unordered multi-indices ATDD’ 18, Contractibility of a persistence map preimage 13

Generalization - set of not ordered multi-indices ATDD’ 18, Contractibility of a persistence map preimage 14

Our first important result ATDD’ 18, Contractibility of a persistence map preimage 15

Lets apply theorems from the previous slides ATDD’ 18, Contractibility of a persistence map preimage 16

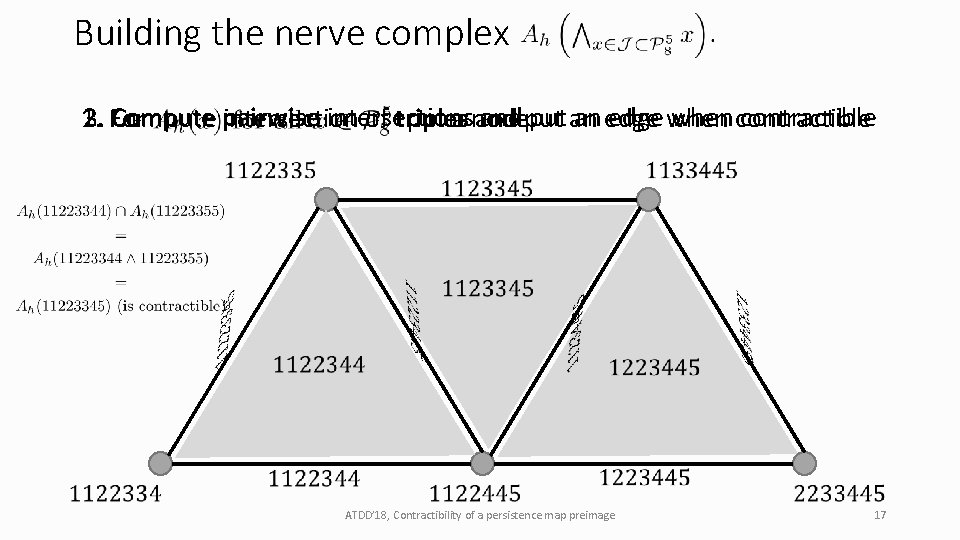
Building the nerve complex 2. Compute pairwise intersections and put an edge when contractible 1. For put a node. 3. Compute intersection of triples and put an edge when contractible ATDD’ 18, Contractibility of a persistence map preimage 17

The story is not yet over, but there is a happy end… HA ! I see that this nerve complex is contractible Great ! But wait, how to generalize the construction of the nerve complex to prove its contractibility in general ? ATDD’ 18, Contractibility of a persistence map preimage 18