Contrabass Clarinet Physical Model MMI 504 Audio Synthesis

Contrabass Clarinet Physical Model MMI 504 Audio Synthesis and Analysis Final Project Nicholas J. Bryan and Trenton C. Watkins

Objectives n n n Understand the fundamentals behind basic clarinet physical models Implement a physical model in Matlab Create user friendly graphical user interface using GUIDE

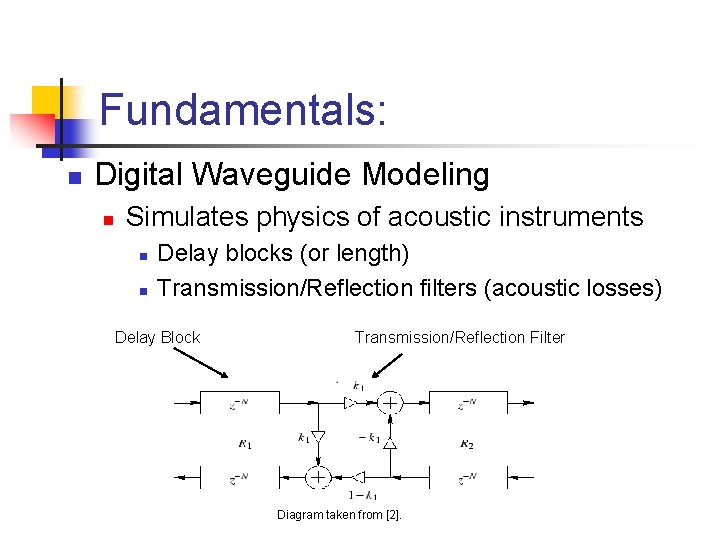
Fundamentals: n Digital Waveguide Modeling n Simulates physics of acoustic instruments n n Delay blocks (or length) Transmission/Reflection filters (acoustic losses) Delay Block Transmission/Reflection Filter Diagram taken from [2].

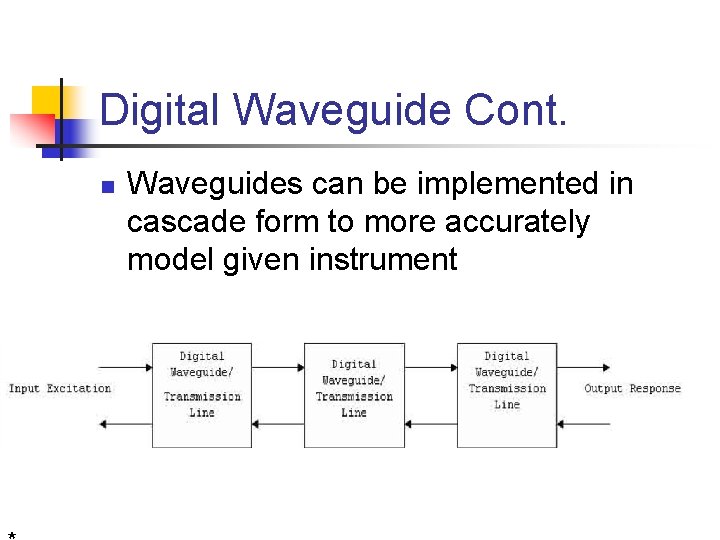
Digital Waveguide Cont. n Waveguides can be implemented in cascade form to more accurately model given instrument

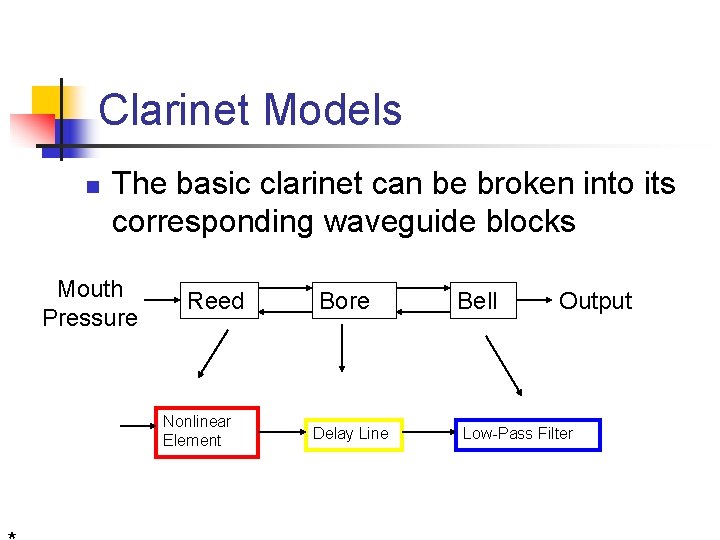
Clarinet Models n The basic clarinet can be broken into its corresponding waveguide blocks Mouth Pressure Reed Nonlinear Element Bore Delay Line Bell Output Low-Pass Filter

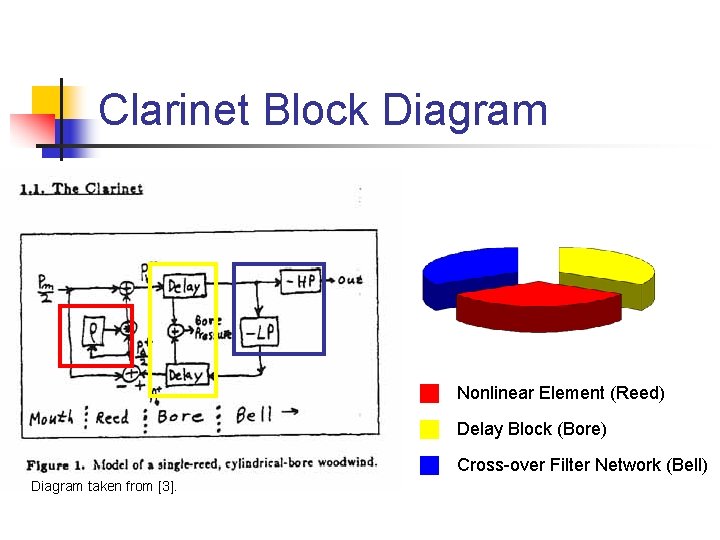
Clarinet Block Diagram Nonlinear Element (Reed) Delay Block (Bore) Cross-over Filter Network (Bell) Diagram taken from [3].

Reed: Nonlinear Element) n Creates the oscillation of the instrument n n Mouth pressure as input signal Uses lookup table as a method of approximating the vibration of the reed If pressure is too high, reed value clips Matlab function: reedtable. m n n Increased slope parameter to simulate increased reed stiffness Scales pressure as a function of reed Fig. Reed table look-up

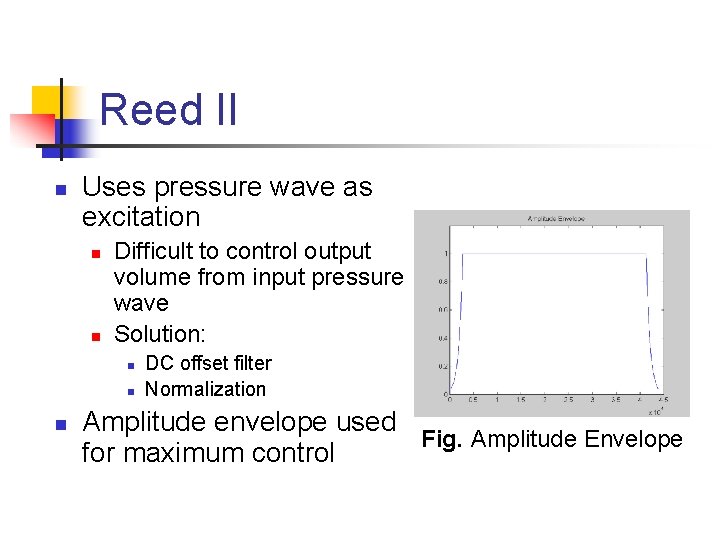
Reed II n Uses pressure wave as excitation n n Difficult to control output volume from input pressure wave Solution: n n n DC offset filter Normalization Amplitude envelope used Fig. Amplitude Envelope for maximum control

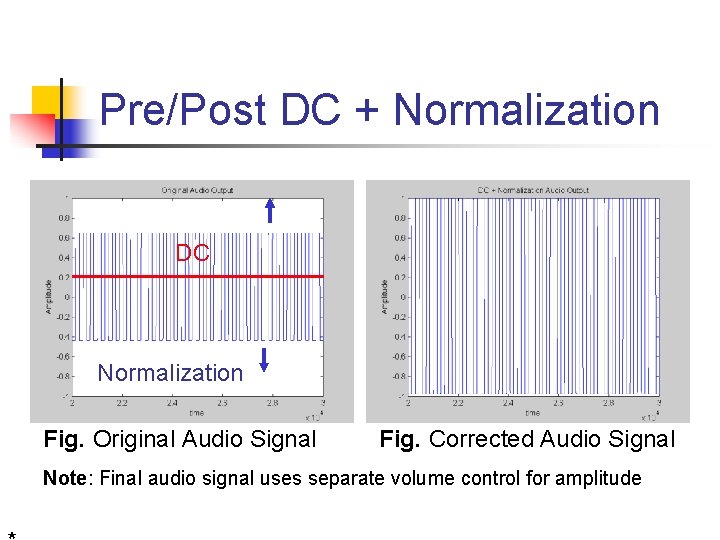
Pre/Post DC + Normalization DC Normalization Fig. Original Audio Signal Fig. Corrected Audio Signal Note: Final audio signal uses separate volume control for amplitude

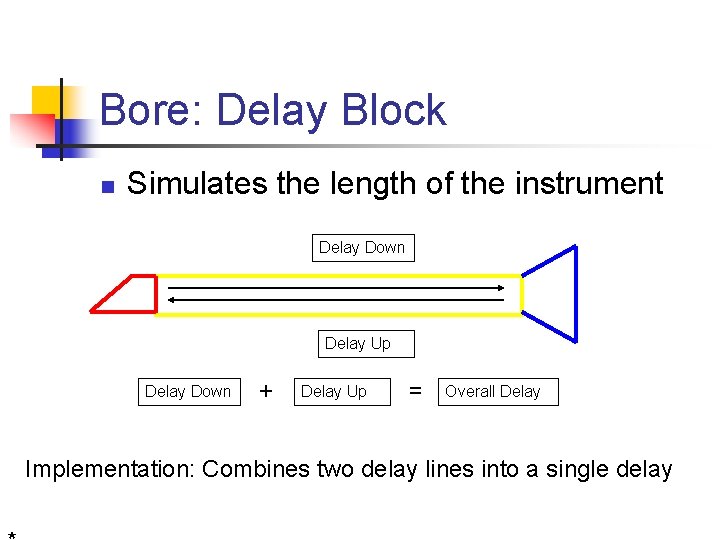
Bore: Delay Block n Simulates the length of the instrument Delay Down Delay Up Delay Down + Delay Up = Overall Delay Implementation: Combines two delay lines into a single delay

Bell: Cross-Over Filter n Low frequencies get reflected n n As the delay line reflects the pressure wave back to the reed losses occur For a clarinet, the cross over is appr. 1500 Hz The filter cutoff required a lower cutoff for contrabass simulations High frequencies are transmitted Fig. 8 th order FIR moving average filter Fig. 16 th order FIR moving average filter HP LP Audio Out

Matlab Implementation n n Initial design using functions and script files Integration into a user-friendly graphical interface n Music Application n n Tempo, Note duration, Pitch, Volume AB comparison with recorded contrabass

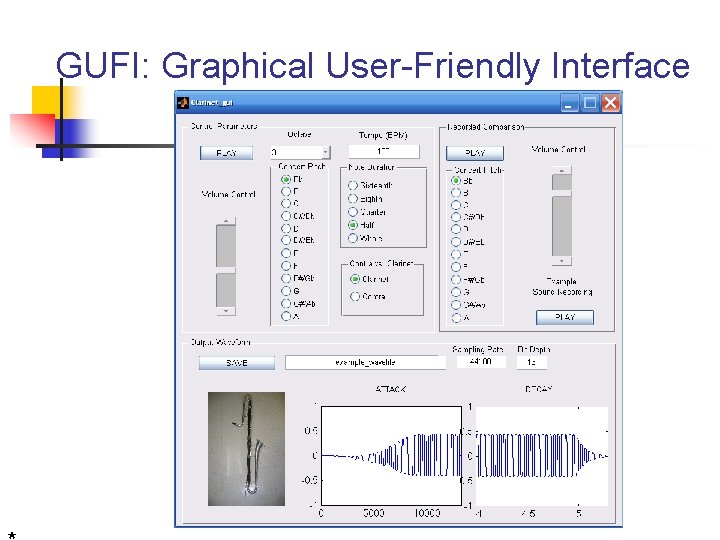
GUFI: Graphical User-Friendly Interface

Pitch/Duration Considerations n n Use 12 value lookup table Multiply by 2 to the power of octave n n Pitch = Lookup*2^Octave Convert BPM into # of samples n n Samples = fs*note_value*60/BPM ie. Samples = 44100(sample/sec)*60(sec/min)/100(beats/min)*1(quarter note)

Conclusions n n n Reflection filter needs careful consideration Low frequency synthesis diverges from the typical clarinet model at low frequencies GUIDE provides an easy development environment for Matlab graphics

References 1. 2. 3. 4. 5. Cook, Perry R. Scavone, Gary P. “The Synthesis Tool. Kit in C++ (STK)”, http: //ccrma. stanford. edu/software/stk/ Smith, Julius O. “Woodwinds”, http: //ccrma. stanford. edu/~jos/pasp/Woodwinds. html Smith, Julius O. “Efficient Simulations of the Reed-Bore and Bow-String Mechanisms”, Proceedings of the 1986 International Computer Music Conference, 1986, pp. 275 -280. Mc. Intyre, M. E. , Schumacher, R. T. and Woodhouse, J. , "On the Oscillations of Musical Instruments, " Journal of the Acoustical Society of America, 74(5), 1983, pp. 1325 -1345. Boulanger, Richard. “The Csound Book”, MIT Press 2000